
Modeling,Computation,Simulation, Designing and Screening of New Materials Xiaobin Niu University of Electronic Science and Technology of China 4/8/2020 2
Modeling, Computation, Simulation, Designing and Screening of New Materials Xiaobin Niu University of Electronic Science and Technology of China 4/8/2020 2

Outline > Design materials using computation > Mathematical models in material science > Monte Carlo Method > Molecular Dynamics
Outline 0.0 ➢ Design materials using computation ➢ Mathematical models in material science ➢ Monte Carlo Method ➢ Molecular Dynamics

Design materials using computation National Academy of Sciences(1995) The phrase "materials by design"with an increasingly theoretical component to the design process,is becoming a reality. Researchers are thus using theory and computation to "design" materials. "n "v ce TS HM Tm Yh Lu Materials Design
2.0 Design materials using computation National Academy of Sciences (1995) The phrase “materials by design” with an increasingly theoretical component to the design process, is becoming a reality. Researchers are thus using theory and computation to “design” materials

Outline > Design materials using computation > Multiscale coupling > Materials Genome and materials informatics > Perspective
Outline 0.0 ➢ Design materials using computation ➢ Multiscale coupling ➢ Materials Genome and materials informatics ➢ Perspective

Role of computational materials science Understanding Prediction How,why,where of phenomenon Parameter values,new phenomena How does H diffuse through A? What is the diffusivity of H in A? Why is A harder than B? ·How hard is A? ·Where does A bind to B? Will A bind to B and how strongly? Design new materials. Shorten the materials development cycle Reduce the fabricating cost of materials
2.1 Role of computational materials science How, why, where of phenomenon • How does H diffuse through A? • Why is A harder than B? • Where does A bind to B? Understanding Prediction Parameter values, new phenomena • What is the diffusivity of H in A? • How hard is A? • Will A bind to B and how strongly? • Design new materials. • Shorten the materials development cycle. • Reduce the fabricating cost of materials
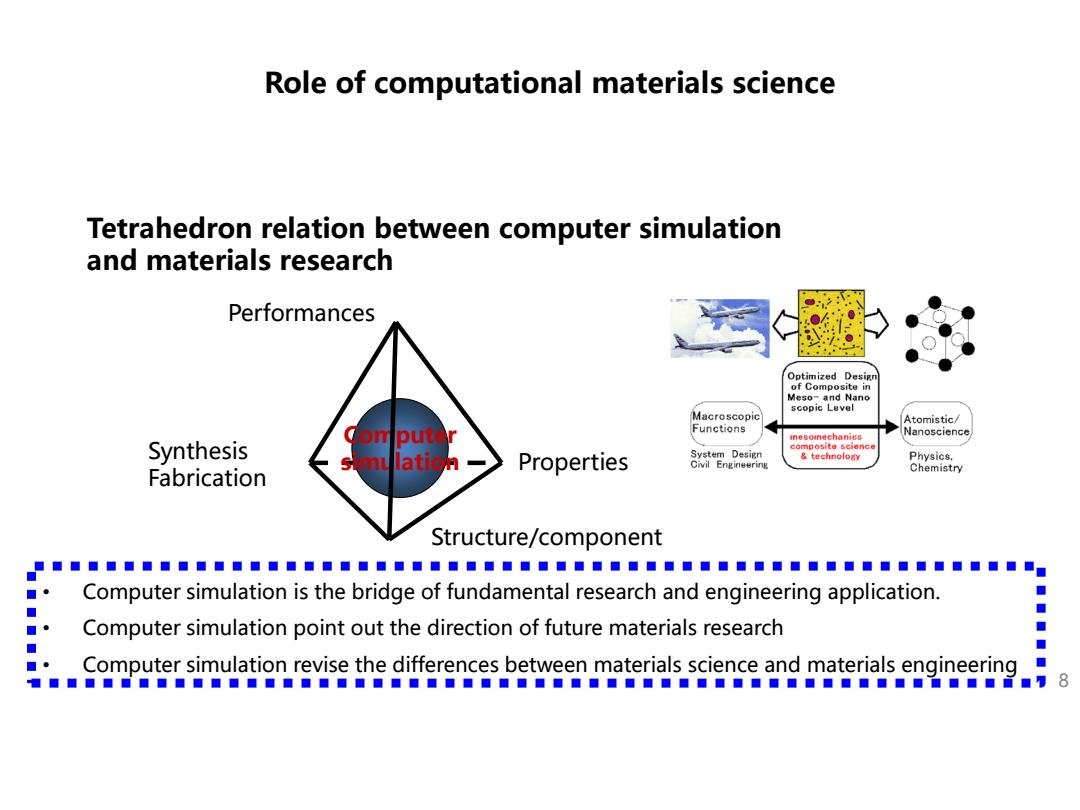
Role of computational materials science Tetrahedron relation between computer simulation and materials research Performances Optimized Desig of Composite in Meso-and Nano scopic Level Macroscopic Atomistic/ gomputr Functions 1门8参ON门echan花0 Nanoscience Synthesis composite scienc。 Properties System Design &t chnolo Civil Engineering Physics. Fabrication Chemistry Structure/component ■■■■■■■■■■■■■■■■■■■■■■■目■■■■■■ Computer simulation is the bridge of fundamental research and engineering application. ◆ ■。 Computer simulation point out the direction of future materials research ◆ ■ ◆ ■。 Computer simulation revise the differences between materials science and materials engineering 1■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■古■18
Tetrahedron relation between computer simulation and materials research 8 Performances Computer simulation Synthesis Fabrication Structure/component Properties 2.1 • Computer simulation is the bridge of fundamental research and engineering application. • Computer simulation point out the direction of future materials research • Computer simulation revise the differences between materials science and materials engineering Role of computational materials science

Recognization of computational materials The Nobel Prize in Chemistry 1998 Walter Kohn John Pople Prize motivation:"for his Prize motivation:"for development of the density his development of functional theory." computational methods in quantum chemistry." 9
9 The Nobel Prize in Chemistry 1998 Recognization of computational materials 2.2 Walter Kohn Prize motivation: "for his development of the density functional theory." John Pople Prize motivation: "for his development of computational methods in quantum chemistry
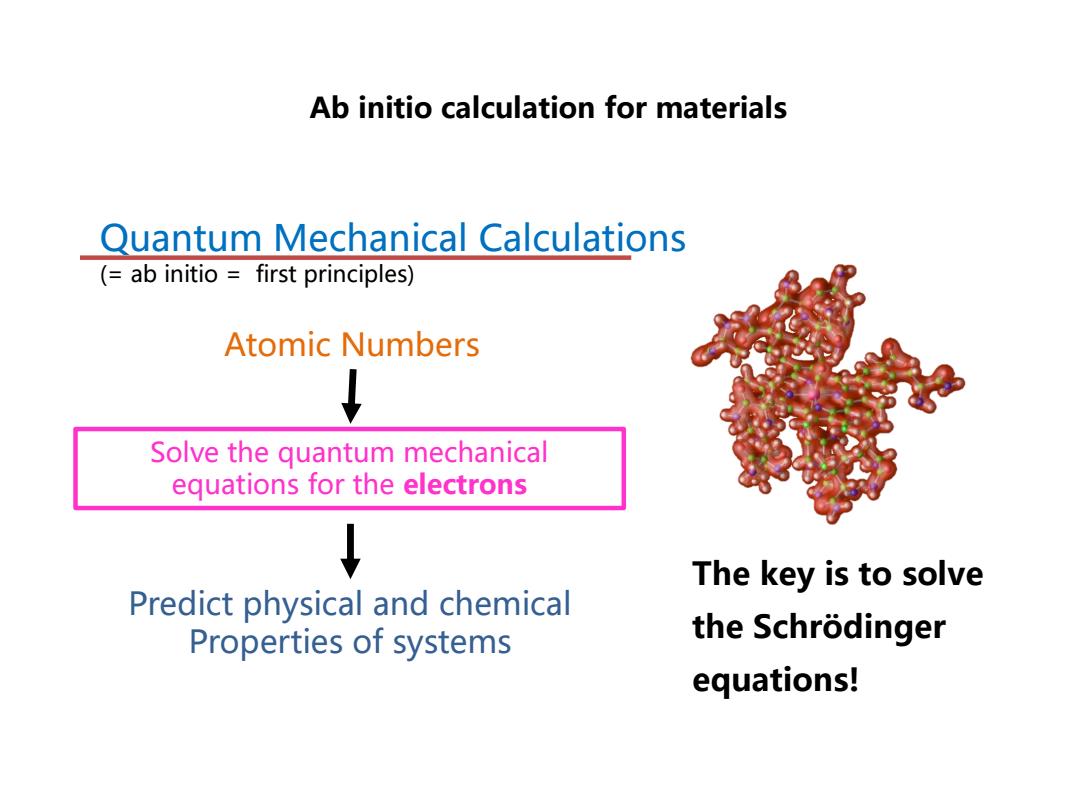
Ab initio calculation for materials Quantum Mechanical Calculations (=ab initio first principles) Atomic Numbers ↓ Solve the quantum mechanical equations for the electrons The key is to solve Predict physical and chemical Properties of systems the Schrδdinger equations!
Ab initio calculation for materials Quantum Mechanical Calculations (= ab initio = first principles) The key is to solve the Schrödinger equations! Atomic Numbers Solve the quantum mechanical equations for the electrons Predict physical and chemical Properties of systems 2.3
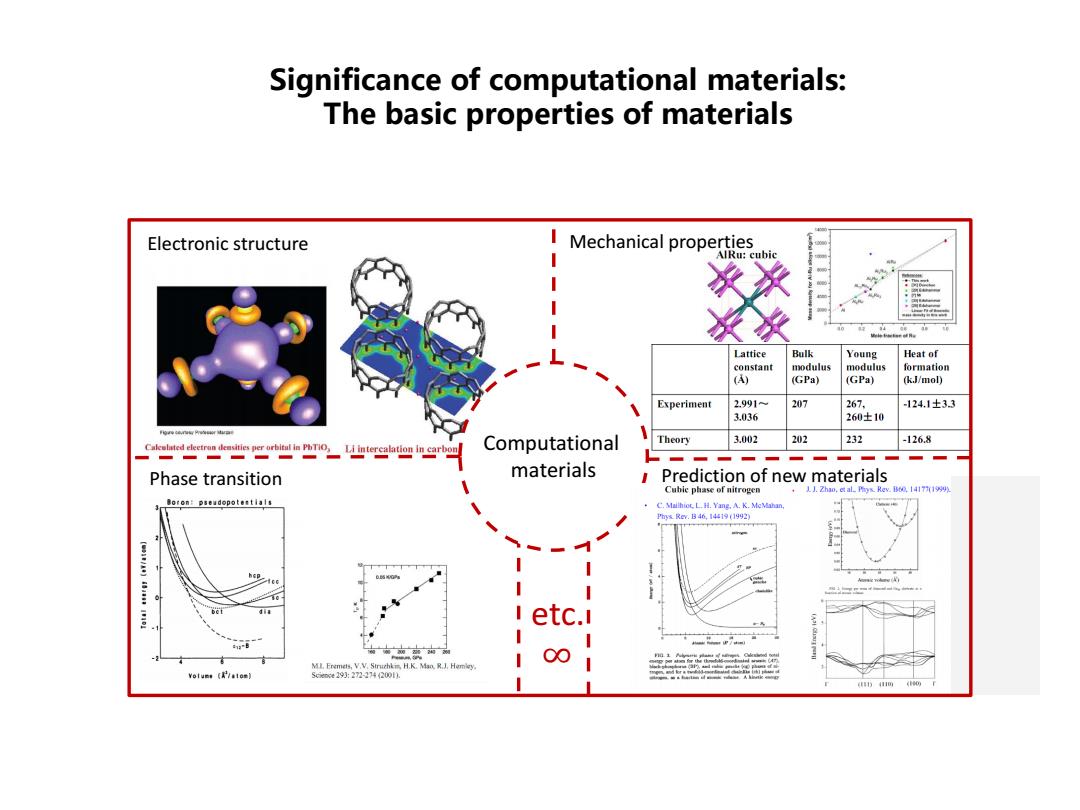
Significance of computational materials: The basic properties of materials Electronic structure Mechanical properties AlRu:cubic Lattice Bulk Young Heat of constant modulus modulus formation (A) (GPa) (GPa) (k.J/mol) Experiment 2.991 207 267, 124.1±33 3.036 260±10 Computational Theory 3.002 202 232 -126.8 Phase transition materials Prediction of new materials Cuhie phase of nitrogen 1J.Zhao,et al_Phys.Rev.Bt0.14171999 Boron:pseudopotestials C.Maithioc L.H.Yang.A.K.MeMahan. hkRe.B46,1419(1992 2 ..: i etc.i sna-B 00 ML.Eremets,V.V.Struchki H.K.Mao.R.J.Hemley. S3oce293:27217420011. pen
Significance of computational materials: The basic properties of materials 2.4 Electronic structure Mechanical properties Computational materials Phase transition Prediction of new materials etc. ∞
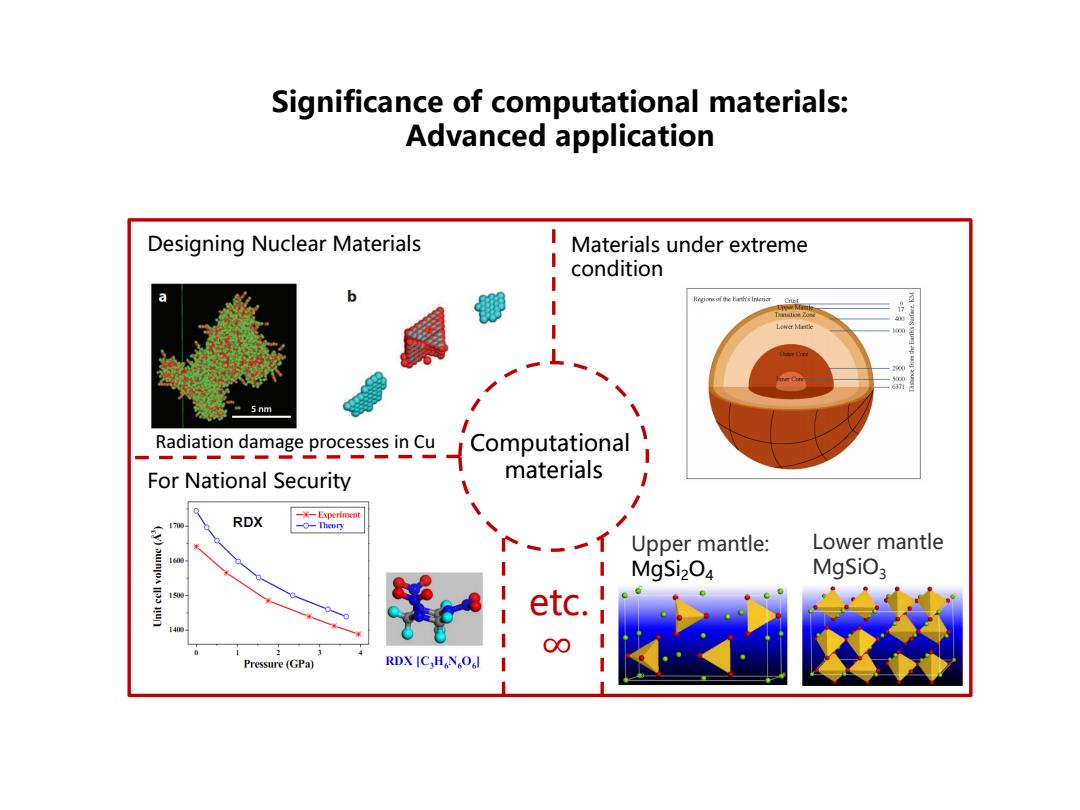
Significance of computational materials: Advanced application Designing Nuclear Materials Materials under extreme condition b Region of the Beh's Irtericr Lower Mecle 5nm Radiation damage processes in Cu Computational For National Security materials 1 RDX -米一Exp优 --Theory (y) 八 Upper mantle: Lower mantle MgSi2O4 MgSiO: 1500- etc. Pressure(GPa) RDX [C,H N。O
Significance of computational materials: Advanced application Computational materials etc. ∞ Designing Nuclear Materials Materials under extreme condition For National Security Upper mantle: MgSi2O4 Lower mantle MgSiO3 Radiation damage processes in Cu 2.4