
ARBEAPE 材料与能源学院 never forget how to dr School of Materials and Energy 《材料分子结构分析》 5. 红外光谱 Infrared Spectroscopy uvalp o1 moy 刘钰 电子科技大学 2021年2022年春季
5. 红外光谱 刘 钰 电子科技大学 2021年-2022年 春季 Infrared Spectroscopy 《材料分子结构分析》 1

never forget how to dream 目绿 5.1 红外吸收光谱概述 5.2 红外光谱的基本原理 5.3 影响红外吸收峰的因素 5.4 典型红外谱带吸收范围 5.5 各类化合物的特征红外吸收 5.6 红外光谱仪 5.7 红外光谱试样制备 5.8 红外光谱的解析 5.9 红外光谱的应用 I 2
目录 5.1 红外吸收光谱概述 5.2 红外光谱的基本原理 5.3 影响红外吸收峰的因素 5.4 典型红外谱带吸收范围 5.5 各类化合物的特征红外吸收 5.6 红外光谱仪 5.7 红外光谱试样制备 5.8 红外光谱的解析 5.9 红外光谱的应用 2
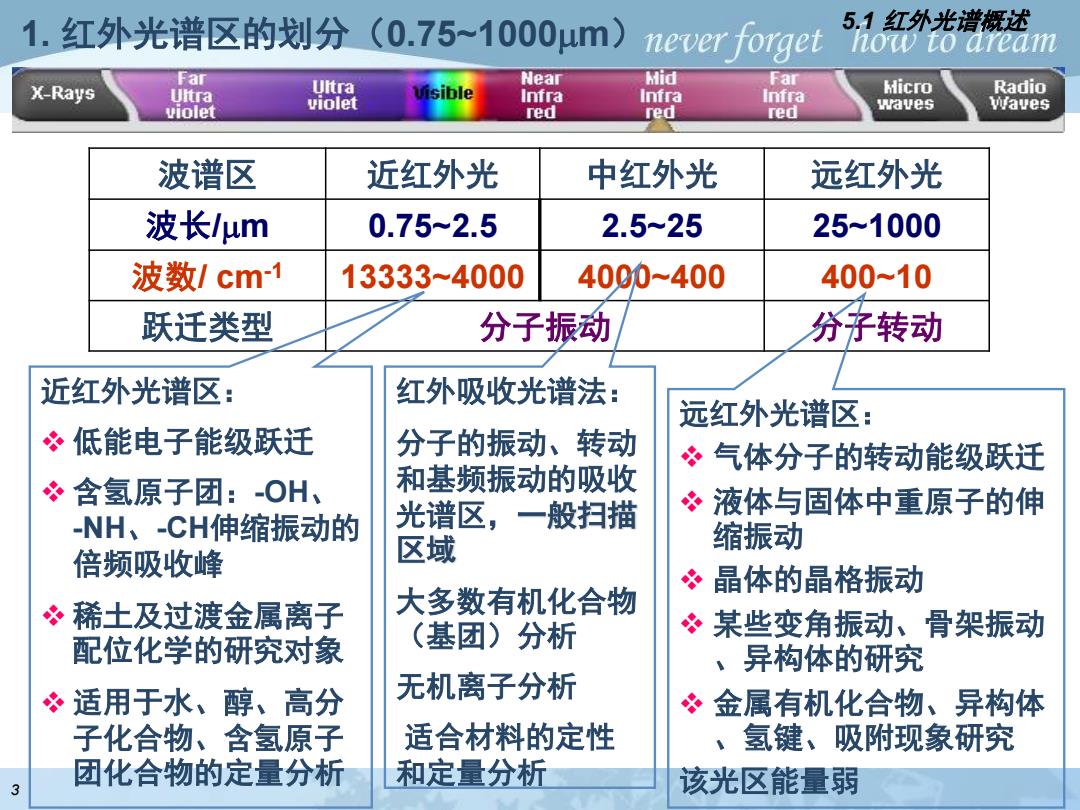
1.红外光谱区的划分(0.75~1000um) never forget 5.1红外光谱概述 how to aream Far Ultra Near Mid Far X-Rays Ultra Infra Infra Infra Micro Radio violet violet red red red waves Waves 波谱区 近红外光 中红外光 远红外光 波长um 0.75-2.5 2.5-25 25~1000 波数/cm-1 13333-4000 4000-400 400-10 跃迁类型 分子振动 分子转动 近红外光谱区: 红外吸收光谱法: 远红外光谱区: 冬低能电子能级跃迁 分子的振动、转动 ?气体分子的转动能级跃迁 含氢原子团:-OH、 和基频振动的吸收 ?液体与固体中重原子的伸 -NH、-CH伸缩振动的 光谱区,一般扫描 缩振动 倍频吸收峰 区域 冬晶体的晶格振动 冬稀土及过渡金属离子 大多数有机化合物 配位化学的研究对象 (基团)分析 冬某些变角振动、骨架振动 、异构体的研究 冬适用于水、醇、高分 无机离子分析 ?金属有机化合物、异构体 子化合物、含氢原子 适合材料的定性 、氢键、吸附现象研究 团化合物的定量分析 和定量分析 3 该光区能量弱
波谱区 近红外光 中红外光 远红外光 波长/m 0.75~2.5 2.5~25 25~1000 波数/ cm-1 13333~4000 4000~400 400~10 跃迁类型 分子振动 分子转动 近红外光谱区: ❖ 低能电子能级跃迁 ❖ 含氢原子团:-OH、 -NH、-CH伸缩振动的 倍频吸收峰 ❖ 稀土及过渡金属离子 配位化学的研究对象 ❖ 适用于水、醇、高分 子化合物、含氢原子 团化合物的定量分析 红外吸收光谱法: 分子的振动、转动 和基频振动的吸收 光谱区,一般扫描 区域 大多数有机化合物 (基团)分析 无机离子分析 适合材料的定性 和定量分析 远红外光谱区: ❖ 气体分子的转动能级跃迁 ❖ 液体与固体中重原子的伸 缩振动 ❖ 晶体的晶格振动 ❖ 某些变角振动、骨架振动 、异构体的研究 ❖ 金属有机化合物、异构体 、氢键、吸附现象研究 该光区能量弱 1. 红外光谱区的划分(0.75~1000m) 5.1 红外光谱概述 3
2.红外光谱的定义 never forget 5.1红外光请概述 how to aream 当样品受到频率连续变化的 红外光照射时,分子吸收其中 一些频率的辐射,分子振动或 转动引起偶极矩的净变化,使 振-转能级从基态跃迁到激发态, 相应于这些区域的透射光强减 弱,记录百分透过率对波数 或波长的曲线,即红外光谱。 分子振动吸收光谱 分子转动吸收光谱 红外光谱又称分子振动-转动 △E分r=△E振动十△E转动 光谱,属分子吸收光谱。 △E振动≈0.05~1eV, 2振动≈25~1.25业m △E转动≈0.005~0.05eV, 转动≈250~25业m 4
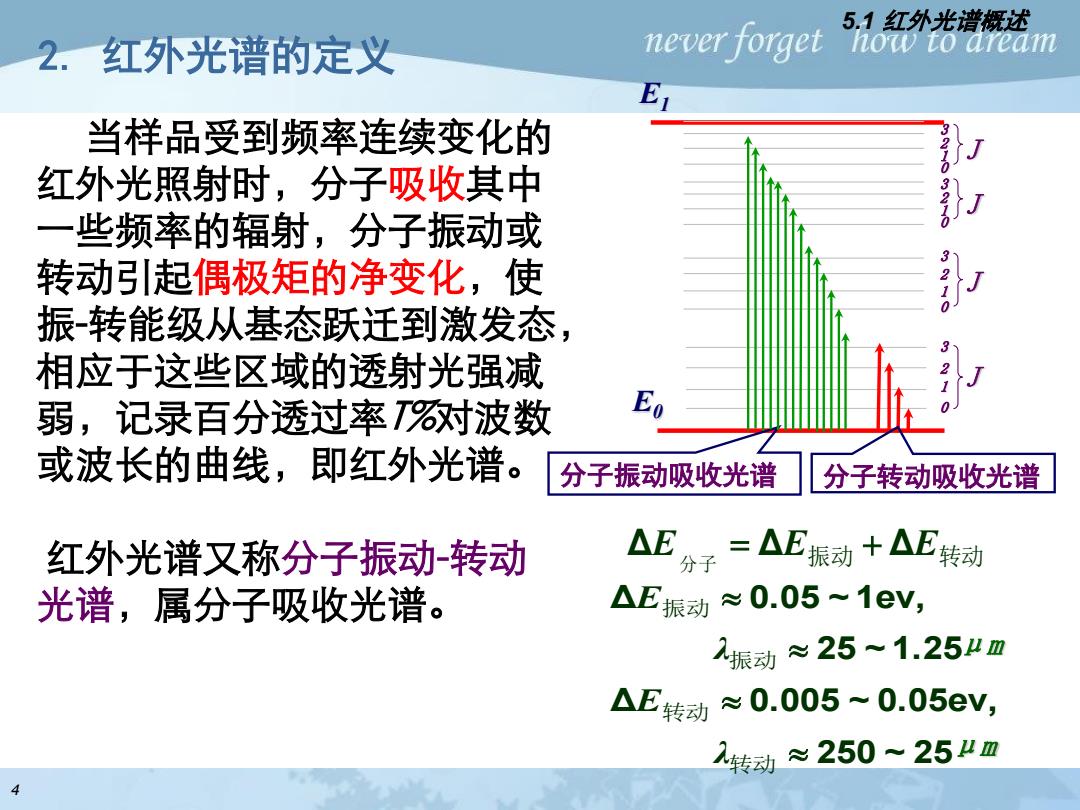
2. 红外光谱的定义 4 当样品受到频率连续变化的 红外光照射时,分子吸收其中 一些频率的辐射,分子振动或 转动引起偶极矩的净变化,使 振-转能级从基态跃迁到激发态, 相应于这些区域的透射光强减 弱,记录百分透过率T%对波数 或波长的曲线,即红外光谱。 红外光谱又称分子振动-转动 光谱,属分子吸收光谱。 5.1 红外光谱概述 E1 E0 1 J 0 2 3 J 0 2 3 1 J 0 2 3 1 J 0 2 3 1 分子振动吸收光谱 分子转动吸收光谱 ( ) (Δ Δ ) Δ Δ Δ 振动 转动 振动 转动 分子 振动 转动 hc / λ λ h ν ν E E E = + = + = + 250 ~ 25 Δ 0.005 ~ 0.05ev, 25 ~ 1.25 Δ 0.05 ~ 1ev, 转动 转动 振动 振动 λ E λ E μm μm
5.1红外光谱概述 never forget how to aream 3.红外光谱的表示方法 A/um 波数即波长的倒数, 2.5 6 891012162025 单位(cm);表示单位 长度的光中所含光波的 数目。 武 波数(cm)=104/n.(μm) T% ×100 % Io 40003600320028002400200018001600140012001000800 600 ()仲丁醇的红外光谱 o/cm-l I:表示透过光的强度; 纵坐标:百分透光率(T%),表示吸收峰强度,T↓, I:表示入射光的强度。 表明吸收的越好,故曲线低谷表示是一个好的吸收带。 横坐标:波长(μm)或波数(yoro/cm1),表明吸收峰 的位置 峰强:Vs(Very strong):很强;s(strong): 强 m (medium):中强;w(weak):弱 峰形:表示形状的为宽峰、尖峰、肩峰、双峰等 双峰 宽峰 尖蜂 肩峰 (分歧峰) 5
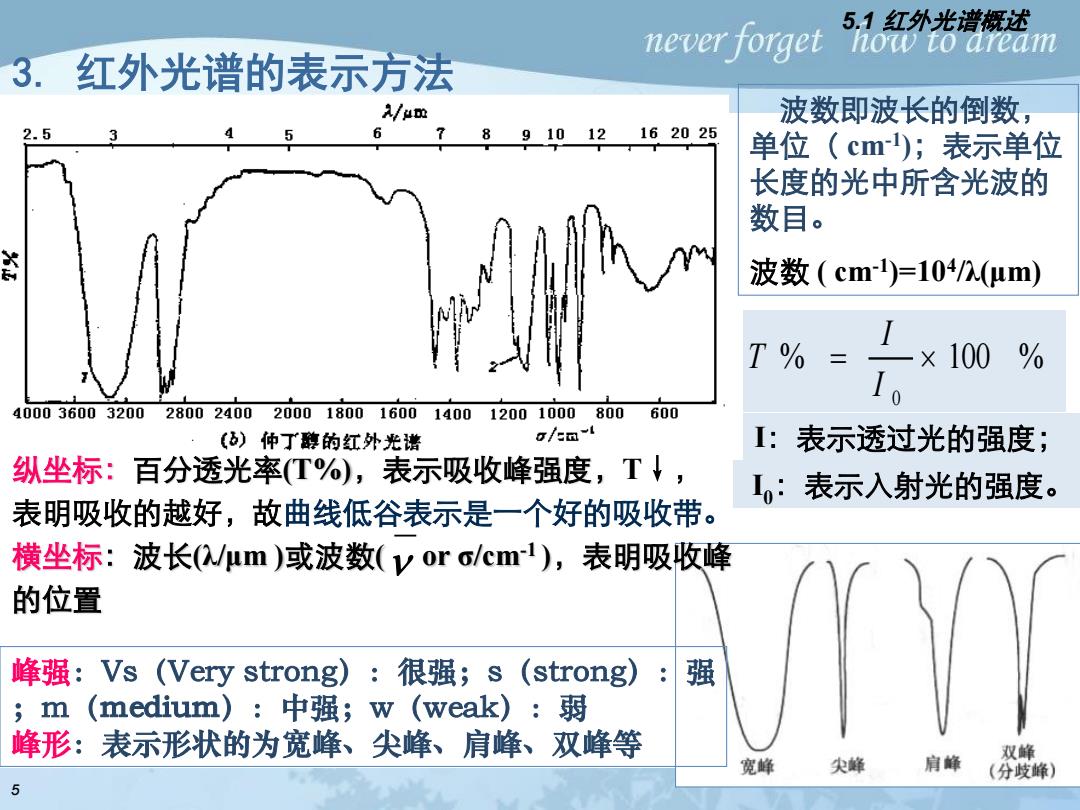
波数即波长的倒数, 单位( cm-1 );表示单位 长度的光中所含光波的 数目。 波数 ( cm-1 )=104 /λ(μm) 3. 红外光谱的表示方法 纵坐标:百分透光率(T%),表示吸收峰强度,T↓, 表明吸收的越好,故曲线低谷表示是一个好的吸收带。 横坐标:波长(λ/μm )或波数( or σ/cm-1 ),表明吸收峰 的位置 峰强:Vs(Very strong):很强;s(strong):强 ;m( ):中强;w(weak):弱 峰形:表示形状的为宽峰、尖峰、肩峰、双峰等 % 100 % 0 = I I T I:表示透过光的强度; I 0:表示入射光的强度。 5.1 红外光谱概述 5

never forget 5.1红外光谱概述 how to aream 4.红外光谱的特点 (1)依据样品吸收谱带的位置、强度、形状、个数,推测分子 中某种官能团或化学键的存在与否,推测官能团的邻近基团,确 定化合物结构 (2)不破坏样品, 对任何样品的存在状态都适用,如气体、液 体、可研细的固体或薄膜似的固体都可以分析,测定方便,制样 简单 (3)特征性高。对不同结构的化合物可给出特征性的谱图,也 叫“分子指纹光谱” (4)分析时间短。普通红外光谱做一个样可在10分钟内完成, 傅里叶变换红外光谱仪一秒钟以内就可完成扫描 (5)样品用量少,可回收。一次约1-5mg,甚至几十微克 (6)方便与其它类型仪器联用,进行多组分分析 6
4. 红外光谱的特点 6 (1)依据样品吸收谱带的位置、强度、形状、个数,推测分子 中某种官能团或化学键的存在与否,推测官能团的邻近基团,确 定化合物结构 (2) 不破坏样品,对任何样品的存在状态都适用,如气体、液 体、可研细的固体或薄膜似的固体都可以分析,测定方便,制样 简单 (3)特征性高。对不同结构的化合物可给出特征性的谱图,也 叫“分子指纹光谱” (4)分析时间短。普通红外光谱做一个样可在10分钟内完成, 傅里叶变换红外光谱仪一秒钟以内就可完成扫描 (5)样品用量少,可回收。一次约1-5mg,甚至几十微克 (6)方便与其它类型仪器联用,进行多组分分析 5.1 红外光谱概述

never forget 5.1红外光谱概述 how to aream 5.红外光谱的应用 定性: 与紫外、核磁、质谱相结合,解析 材料的分子结构。 定量: 依据特征峰的强度,朗伯一比尔定律 7
5. 红外光谱的应用 7 定性: 与紫外、核磁、质谱相结合,解析 材料的分子结构。 定量: 依据特征峰的强度,朗伯-比尔定律 5.1 红外光谱概述
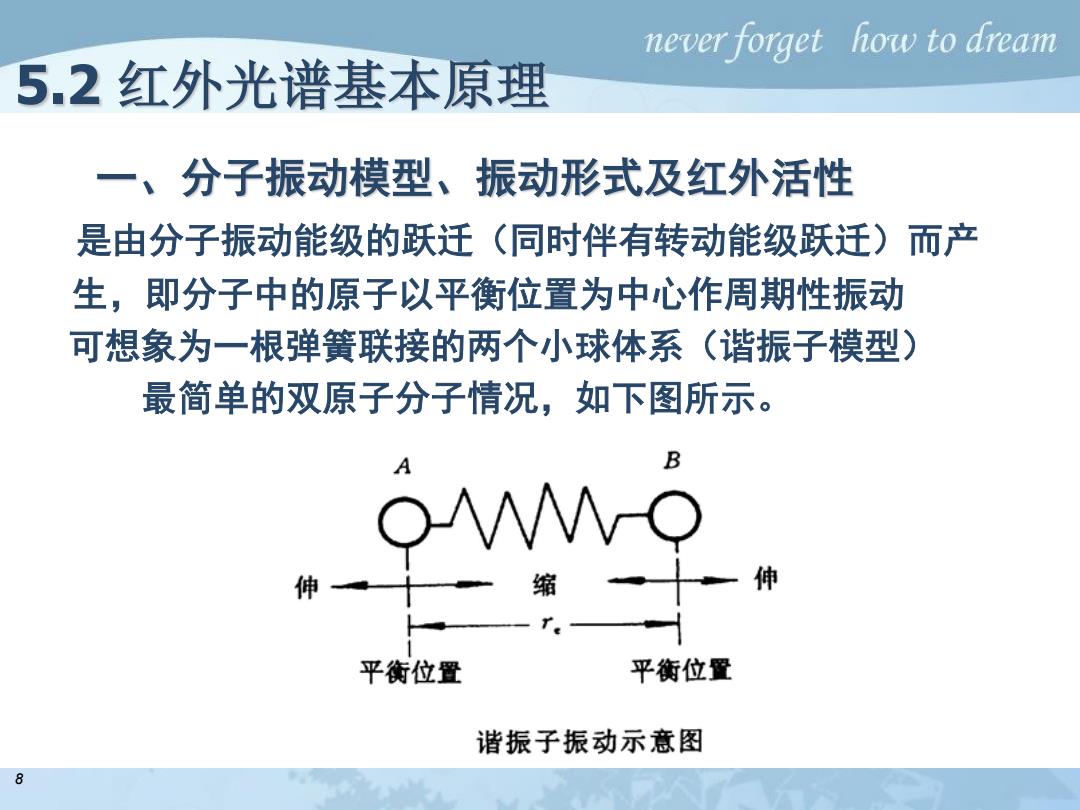
never forget how to dream 5.2红外光谱基本原理 一、分子振动模型、振动形式及红外活性 是由分子振动能级的跃迁(同时伴有转动能级跃迁)而产 生,即分子中的原子以平衡位置为中心作周期性振动 可想象为一根弹簧联接的两个小球体系(谐振子模型) 最简单的双原子分子情况,如下图所示。 B 缩 伸 平衡位置 平衡位置 谐振子振动示意图 8
一、分子振动模型、振动形式及红外活性 是由分子振动能级的跃迁(同时伴有转动能级跃迁)而产 生,即分子中的原子以平衡位置为中心作周期性振动 可想象为一根弹簧联接的两个小球体系(谐振子模型) 最简单的双原子分子情况,如下图所示。 5.2 红外光谱基本原理 8

5.2红外光谱基本原理 never forget T how to aream 1、双原子分子振动方程式 根据虎克定律: h K 2π k--化学键的力常数(Ncm),与键能和键长有关; --双原子的折合质量:μ=m1m2/(m1+m2) M是折合相对原子质量 分子的振动能级(量子化): E振(+l/2)hv ν:化学键的振动频率; V:振动量子数(V=0、1、2.…),当V=0时,E0,称为零点能。 9
1、双原子分子振动方程式 分子的振动能级(量子化): E振动=(V+1/2)hν ν:化学键的振动频率; V: 振动量子数(V=0、1、2......),当V=0时,E≠0,称为零点能。 根据虎克定律: k-----化学键的力常数(N/cm) ,与键能和键长有关; μ---双原子的折合质量: μ =m1m2/(m1+m2 ) 5.2 红外光谱基本原理 𝑣 − (cm−1) = 1 λ = 1 2π𝐶 𝑘 μ = 130𝟑 𝑘 M 9 M是折合相对原子质量

5,2红外光谱基本原理 never forget 7 how to aream 任意两个能级间的能量差为: h K E=△VIhv=△V 2元 当△V=1时,0→1振动能级的跃迁,称为基本振动频率 或基频吸收带。 折合质量和键力常数是影响基本振动频率的直接因素。 K越大,或μ越小,或化学键的振动频率越高,吸收峰 将出现在高波数区;反之,则出现在低波数区。 10
任意两个能级间的能量差为: κ 2 h E = Vhv = V π μ 当△V =1时,0→ 1振动能级的跃迁,称为基本振动频率 或基频吸收带。 折合质量和键力常数是影响基本振动频率的直接因素。 K 越大,或μ越小,或化学键的振动频率越高,吸收峰 将出现在高波数区;反之,则出现在低波数区。 h 5.2 红外光谱基本原理 10