
南華大乳 UNIVERSITY OF SOUTH CHINA 管理学院 信息管理与信息、系统专业 教学大纲汇编 南华大学教务处 2017年9月
1 管理学院 信息管理与信息系统专业 教学大纲汇编 南华大学教务处 2017 年 9 月

目录 1.学科基础课平台必修课…1 《高等数学B1》课程教学大纲. 《高等数学B1》课程考试大纲 5 《高等数学B2》课程教学大纲 8 《高等数学B2》课程老试大细 15 《线性代数》课程教学大纲」 《概率论与数理统计B》课程教学大纲 1823 《管理学A》课程教学大纲. 0 《统计学A》课程教学大纲 《统计学A》课程考试教学大纲 45 《基础会计学B》课程教学大纲 48 《基础会计学B》课程考试大纲 《市场营销学A》课程教学大纲 55 《市场营销学A》课程考试大纲 63 《信息管理与信息系统专业导论》课程教学大纲, 68 2学科基础课平台选修课, 《经济法0》课程教学大纲 《经济法C》课程考试大纲 《组织行为学》B课程教学大纲 82 《组织行为学》B课程考试大纲。 0 《计算机办公自动化》课程教学大纲。 3 《计算机办公自动化》课程实践教学大纲 《运筹学6》课程教学大纲 %9 《市场调查与分析》课程教学大纲. 10G 《市场调查与分析》课程考试大纲. .110 《市场调查与分析》课程实践教学大纲】 113 《才多档理学B》里程老试大银 115 《创业管理》课程教学大纲。 19 《战略管理B》教学大纲 126 《系统工程学C》课程教学大纲 133 《系统工程学C》课程考试大纲 142 《管理研究方法》课程教学大纲 145 3.专业课平台必修课 《提库原理与应用课程教学大纷 《面向对象程序设计》课程实践教学大纲 160 《电子商务概论》教学大纲. 169 《信息系统开发环境与工具》课程教学大纲 《信息系统开发环墙与T具》课程老试大级 191 《信息系统开发环境与工具》课程实践教学大纲 《信息资源组织与管理》课程教学大纲 《信息资源组织与管理》课程考试大纲。 .207 《管理信息系统》课程教学大纲, .211
I 目 录 1.学科基础课平台必修课 ......................................................... 1 《高等数学 B1》课程教学大纲...................................................................................................... 1 《高等数学 B1》课程考试大纲...................................................................................................... 5 《高等数学 B2》课程教学大纲...................................................................................................... 8 《高等数学 B2》课程考试大纲.................................................................................................... 15 《线性代数》课程教学大纲......................................................................................................... 18 《概率论与数理统计 B》课程教学大纲...................................................................................... 23 《管理学 A》课程教学大纲.......................................................................................................... 30 《统计学 A》课程教学大纲.......................................................................................................... 40 《统计学 A》课程考试教学大纲.................................................................................................. 45 《基础会计学 B》课程教学大纲.................................................................................................. 48 《基础会计学 B》课程考试大纲.................................................................................................. 52 《市场营销学 A》课程教学大纲.................................................................................................. 55 《市场营销学 A》课程考试大纲.................................................................................................. 63 《信息管理与信息系统专业导论》课程教学大纲..................................................................... 68 2.学科基础课平台选修课 ........................................................ 71 《经济法 C》课程教学大纲.......................................................................................................... 71 《经济法 C》课程考试大纲.......................................................................................................... 77 《组织行为学》B 课程教学大纲.................................................................................................. 82 《组织行为学》B 课程考试大纲.................................................................................................. 90 《计算机办公自动化》课程教学大纲......................................................................................... 93 《计算机办公自动化》课程实践教学大纲................................................................................. 96 《运筹学 B》课程教学大纲.......................................................................................................... 99 《市场调查与分析》课程教学大纲........................................................................................... 106 《市场调查与分析》课程考试大纲........................................................................................... 110 《市场调查与分析》课程实践教学大纲................................................................................... 113 《财务管理学 B》课程考试大纲................................................................................................ 115 《创业管理》课程教学大纲....................................................................................................... 119 《战略管理 B》教学大纲............................................................................................................ 126 《系统工程学 C》课程教学大纲................................................................................................ 133 《系统工程学 C》课程考试大纲................................................................................................ 142 《管理研究方法》课程教学大纲............................................................................................... 145 3. 专业课平台必修课 .......................................................... 151 《数据库原理与应用 A》课程教学大纲.................................................................................... 151 《面向对象程序设计》课程实践教学大纲............................................................................... 160 《电子商务概论》教学大纲....................................................................................................... 169 《信息系统开发环境与工具》课程教学大纲........................................................................... 181 《信息系统开发环境与工具》课程考试大纲........................................................................... 191 《信息系统开发环境与工具》课程实践教学大纲................................................................... 197 《信息资源组织与管理》课程教学大纲................................................................................... 202 《信息资源组织与管理》课程考试大纲................................................................................... 207 《管理信息系统》课程教学大纲............................................................................................... 211

《管理信息系统》课程考试大纲。 216 《管理信息系统》课程实践教学大纲 218 《信息专业实习》课程教学大纲 444444444444444444444444444444 《信管毕业实习》教学大织 23 信总管理与信总系统专业毕业设计(论文)教学大纲.」 230 4.专业课平台选修课.…234 《平面图像处理》课程教学大纲】 234 《网页设计与制作》课程教学大纲 248 《网页设计与制作》考 试课程教学大纲 5 《网页设计与制作》课程实践教学大纲 《网页设计与制作》课程实训教学大纲。 .267 《信息经济学》课程教学大纲 .275 《操作系续》课程教学大织 281 《操作系统》课程考试教学大纲 《信息检索与利用》课程教学大纲 《信息检索与利用》课程实践教学大纲. 300 电子商务支付与安全教学大纲 .304 《数据挖据与商务智能》课程教学大纲 300 《数据挖掘与商务智能》课程实践教学大纲 313 《信息服务与用户》课程教学大织 317 《信息服务与用户》课程实践大纲 321 《软件工程》课程教学大纲 323 《软件工程》课程考试大纲」 331 《信息分析与预测》课程教学大纲 335 《信息分析与预测》课程考试大纲 《移动开发技术》课程教学大纲 《信息系统项目管理》课程教学大纲 347 《信息系统项目管理》课程考试大纲 354 《信息资源知识产权》课程教学大纲 150 《电子政务》教学大纲 《决策支持系统》课程教学大纲 367 《信管专业英语》课程教学大纲 370 《信管专业认知调查》实习教学大纲 .375 《信息管理与信息系统》专业学年论文教学大纲 377 《数据结构》课程设计教学大纲 381 《管理信息系统》课程设计教学大纲 《操作系统》课程设计教学大纲 385 《网页设计与制作》课程实训教学大纲. 388 《商业数据分析》实训教学大纲。 396 《新创业剑意实加》实习大纲 .403
II 《管理信息系统》课程考试大纲............................................................................................... 216 《管理信息系统》课程实践教学大纲....................................................................................... 218 《信息专业实习》课程教学大纲............................................................................................... 223 《信管毕业实习》教学大纲....................................................................................................... 227 信息管理与信息系统专业毕业设计(论文)教学大纲........................................................... 230 4. 专业课平台选修课 .......................................................... 234 《平面图像处理》课程教学大纲............................................................................................... 234 《网页设计与制作》课程教学大纲........................................................................................... 248 《网页设计与制作》考试课程教学大纲................................................................................... 255 《网页设计与制作》课程实践教学大纲................................................................................... 259 《网页设计与制作》课程实训教学大纲................................................................................... 267 《信息经济学》课程教学大纲................................................................................................... 275 《操作系统》课程教学大纲....................................................................................................... 281 《操作系统》课程考试教学大纲............................................................................................... 290 《信息检索与利用》课程教学大纲........................................................................................... 294 《信息检索与利用》课程实践教学大纲................................................................................... 300 电子商务支付与安全教学大纲................................................................................................... 304 《数据挖掘与商务智能》课程教学大纲................................................................................... 309 《数据挖掘与商务智能》课程实践教学大纲........................................................................... 313 《信息服务与用户》课程教学大纲........................................................................................... 317 《信息服务与用户》课程实践大纲........................................................................................... 321 《软件工程》课程教学大纲....................................................................................................... 323 《软件工程》课程考试大纲....................................................................................................... 331 《信息分析与预测》课程教学大纲........................................................................................... 335 《信息分析与预测》课程考试大纲........................................................................................... 338 《移动开发技术》课程教学大纲............................................................................................... 340 《信息系统项目管理》课程教学大纲....................................................................................... 347 《信息系统项目管理》课程考试大纲....................................................................................... 354 《信息资源知识产权》课程教学大纲....................................................................................... 359 《电子政务》教学大纲............................................................................................................... 362 《决策支持系统》课程教学大纲............................................................................................... 367 《信管专业英语》课程教学大纲............................................................................................... 370 《信管专业认知调查》实习教学大纲....................................................................................... 375 《信息管理与信息系统》专业学年论文 教学大纲................................................................. 377 《数据结构》课程设计教学大纲............................................................................................... 381 《管理信息系统》课程设计教学大纲....................................................................................... 383 《操作系统》课程设计教学大纲............................................................................................... 385 《网页设计与制作》课程实训教学大纲................................................................................... 388 《商业数据分析》实训教学大纲............................................................................................... 396 《创新创业创意实训》实习大纲............................................................................................... 403

1.学科基础课平台必修课 《高等数学B1》课程教学大纲 Higher Mathematics BI 课程编号:130704005 学时:56 学分:3.5 适用对象:经管类 先修课程: 一、课程的性质和任务 本课程是学校经管类各专业的一门必修的重要的公共基础课,是为培养学生的基本素质、学 习后续课程服务的, 通过本课程的学习,逐步培养学生的抽象思维的能力、逻辑推理能力、空间想象能力、自学 能力以及综合运用所学知识分析问题、解决问题的能力,为学生学习后续课程和进一步获得近代 科学技术知识奠定必要的数学基础。 素质要求:素质要求1,3-① 二、教学目的与要求 教学中应认真贯彻“以应用为目的,以必需够用为度”的原则,教学重点放在“掌握概 念,强化应用,培养能力,提高素质”上 教学目的:在课程的教学过程中,要通过各个教学环节逐步培养学生的抽象思维能力、逻辑 推理能力、空间想象能力、数学运算能力、综合解题能力、数学建模与实践能力以及自学能力。 使学生在掌握数学知识的同时,尽量多地理解数学思想、明晰数学方法、建立数学思维。 教学要求:1、使学生掌握本课程的基本概念、基本理论和基本运算,为学习各专业课稻 提供必要的工具:2、逐步培养学生具有比较熟练的基本运算能力、综合运用所学知识分析和 解决实际问题的能力、数学建模及使用计算机求解数学模型的能力、初步抽象概括问题的能 力、自主学习的能力以及一定的逻辑推理能力,使学生在掌握数学知识的同时,尽量多地理解 数学思想、明晰数学方法、建立数学思维。 理解和掌握函数的相关性质、极限的概念、导数与微分的概念、中值定理及导数的应用、 不定积分、定积分:熟练掌握复合函数的复合过程、基本初等函数的简单性质及其图象、两个 重要极限求极限的方法、基本初等函数的导数基本公式、四则运算法则以及复合函数的求导方
1 1.学科基础课平台必修课 《高等数学 B1》课程教学大纲 Higher Mathematics B1 课程编号:130704005 学时:56 学分:3.5 适用对象:经管类 先修课程: 一、课程的性质和任务 本课程是学校经管类各专业的一门必修的重要的公共基础课,是为培养学生的基本素质、学 习后续课程服务的。 通过本课程的学习,逐步培养学生的抽象思维的能力、逻辑推理能力、空间想象能力、自学 能力以及综合运用所学知识分析问题、解决问题的能力,为学生学习后续课程和进一步获得近代 科学技术知识奠定必要的数学基础。 素质要求:素质要求 1,3-① 二、教学目的与要求 教学中应认真贯彻“以应用为目的,以必需够用为度”的原则,教学重点放在“掌握概 念,强化应用,培养能力,提高素质”上。 教学目的:在课程的教学过程中,要通过各个教学环节逐步培养学生的抽象思维能力、逻辑 推理能力、空间想象能力、数学运算能力、综合解题能力、数学建模与实践能力以及自学能力。 使学生在掌握数学知识的同时,尽量多地理解数学思想、明晰数学方法、建立数学思维。 教学要求:1、使学生掌握本课程的基本概念、基本理论和基本运算,为学习各专业课程 提供必要的工具;2、逐步培养学生具有比较熟练的基本运算能力、综合运用所学知识分析和 解决实际问题的能力、数学建模及使用计算机求解数学模型的能力、初步抽象概括问题的能 力、自主学习的能力以及一定的逻辑推理能力,使学生在掌握数学知识的同时,尽量多地理解 数学思想、明晰数学方法、建立数学思维。 理解和掌握函数的相关性质、极限的概念、导数与微分的概念、中值定理及导数的应用、 不定积分、定积分;熟练掌握复合函数的复合过程、基本初等函数的简单性质及其图象、两个 重要极限求极限的方法、基本初等函数的导数基本公式、四则运算法则以及复合函数的求导方

法、洛必达法则求“0/0”、“c/四”、“0X四”、“四-四”、“1四”、“00”和 “®0”型未定式的极限方法、不定积分第一换元法、第二换元法。 三、教学内容 第一章函数与极限 1.基本内容: 函数概念、函数的性质,复合函数:极限,左右极限,无穷小量,无穷大量,极限的四则 运算,两个极限存在准则,两个重要极限:连续性,连续函数的运算性质,基本初等函数和闭区 间上连续函数的性质(最大值,最小值定理和介值定理)。 2.教学基本要求: 理解函数的概念,函数在一点连续的概念:熟悉基本初等函数的性质及其图形:了解反函 数、复合函数概念,极限的eN,e-6定义(对于给出e求N或6不作过高要求),并能在学习 过程中逐步加深对极限思想的理解,两个极限存在准则,无穷小、无穷大概念,初等函数的连续 性:掌握极限四则运算法则及无穷小的比较:知道在闭间区上连续函数的性质:会用两个重要极 限求极限,会判断间断点的类型,能列出简单实际问题中的函数关系。 3.教学重点难点: 函数的概念、极限的。-N,E一6定义:连续函数的性质:两个重要极限求极限,判断间断 点的类型,列出简单实际问题中的函数关系:难点为函数极限的e-N,e-6定义。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第二章导数与微分 1.基本内容: 导数概念,导数的几何意义,可导性与连续性之间的关系,导数的运算法则(四则运算、复 合运算、求反函数导数法则),基本初等函数的导数公式,高阶导数,隐函数的导数,对数求导 法,由参数方程所确定的函数的导数,微分概念及其运算法则(包括一阶微分形式不变性),微 分在近似计算及误差估计中的应用。高阶导数的概念,高阶导数的运算法则,参数方程及隐函数 的高阶导数,高阶微分。 2.教学基本要求: 理解导数和微分概念:熟悉导数和微分的运算法则(包括一阶微分形式不变性)和导数的 基本公式,熟练地求初等函数的一阶,二阶导数:了解导数的几何意义,函数的可导性与连续性 的关系,高阶导数概念:掌握隐函数和参数式所确定的函数的一阶、二阶导数的求法。 3.教学重点难点: 2
2 法、洛必达法则求“0/0”、“∞/ ∞”、“0×∞”、“∞-∞”、“1∞”、“00”和 “∞0”型未定式的极限方法、不定积分第一换元法、第二换元法。 三、教学内容 第一章 函数与极限 1.基本内容: 函数概念、函数的性质,复合函数;极限,左右极限,无穷小量,无穷大量,极限的四则 运算,两个极限存在准则,两个重要极限;连续性,连续函数的运算性质,基本初等函数和闭区 间上连续函数的性质(最大值,最小值定理和介值定理)。 2.教学基本要求: 理解函数的概念,函数在一点连续的概念;熟悉基本初等函数的性质及其图形;了解反函 数、复合函数概念,极限的ε-N,ε-δ定义(对于给出ε求 N 或δ不作过高要求),并能在学习 过程中逐步加深对极限思想的理解,两个极限存在准则,无穷小、无穷大概念,初等函数的连续 性;掌握极限四则运算法则及无穷小的比较;知道在闭间区上连续函数的性质;会用两个重要极 限求极限,会判断间断点的类型,能列出简单实际问题中的函数关系。 3.教学重点难点: 函数的概念、极限的ε-N,ε-δ定义;连续函数的性质;两个重要极限求极限,判断间断 点的类型,列出简单实际问题中的函数关系;难点为函数极限的ε-N,ε-δ定义。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第二章 导数与微分 1.基本内容: 导数概念,导数的几何意义,可导性与连续性之间的关系,导数的运算法则(四则运算、复 合运算、求反函数导数法则),基本初等函数的导数公式,高阶导数,隐函数的导数,对数求导 法,由参数方程所确定的函数的导数,微分概念及其运算法则(包括一阶微分形式不变性),微 分在近似计算及误差估计中的应用。高阶导数的概念,高阶导数的运算法则,参数方程及隐函数 的高阶导数,高阶微分。 2.教学基本要求: 理解导数和微分概念;熟悉导数和微分的运算法则(包括一阶微分形式不变性)和导数的 基本公式,熟练地求初等函数的一阶,二阶导数;了解导数的几何意义,函数的可导性与连续性 的关系,高阶导数概念;掌握隐函数和参数式所确定的函数的一阶、二阶导数的求法。 3.教学重点难点:

理解导数和微分概念,函数的可导性与连续性的关系:高阶导数的概念,高阶导数的运算法 则,参数方程及隐函数的高阶导数,高阶微分。高阶导数概念,导数的几何意义:难点为高阶导 数,高阶微分的求解。 4,教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第三章微分中值定理与导数的应用 1.基本内容: 罗尔定理,格朗日定理,柯西定理,带有拉格朗日余项的泰勒公式。导数的应用,罗必达法 则,函数增减性判定法,函数的极值及其求法,最大值,最小值问题,函数图形的凹凸及其判定 法,拐点及其求法,水平与垂直渐连线,函数图形的描绘,弧微分,求方程近似解的二分法和切 线法。 2.教学基本要求: 理解罗尔定理,拉格朗日定理,函数的极值概念:熟悉柯西定理、泰勒定理:掌握求函数的 极值,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的方法:求方程近似解的二分 法和切线法:能用导数描述一些经济学中的问题,会应用拉格朗日定理,能描绘函数的图形,会 解荷单的最大值和最小值问题 3.教学重点难点: 掌握函数的极值的计算方法,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的 方法。熟悉函数图形的描绘。难点为柯西定理、秦勒定理:函数作图 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第四章不定积分 1.基本内容: 不定积分的概念,性质,基本积分公式,换元积分法,分部积分法,有理函数、三角函数 有理函数及简单的无理函数的积分举例。 2.教学基本要求: 理解不定积分的概念和性质,掌握基本积分公式,换元积分法,分部积分法:了解有理函数 的积分,可化为有理函数的积分。 3.教学重点难点: 不定积分的概念,性质,基本积分公式,换元积分法,分部积分法。第二类换元积分法,有 理函数积分法 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 3
3 理解导数和微分概念,函数的可导性与连续性的关系;高阶导数的概念,高阶导数的运算法 则,参数方程及隐函数的高阶导数,高阶微分。高阶导数概念,导数的几何意义;难点为高阶导 数,高阶微分的求解。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第三章 微分中值定理与导数的应用 1.基本内容: 罗尔定理,格朗日定理,柯西定理,带有拉格朗日余项的泰勒公式。导数的应用,罗必达法 则,函数增减性判定法,函数的极值及其求法,最大值,最小值问题,函数图形的凹凸及其判定 法,拐点及其求法,水平与垂直渐连线,函数图形的描绘,弧微分,求方程近似解的二分法和切 线法。 2.教学基本要求: 理解罗尔定理,拉格朗日定理,函数的极值概念;熟悉柯西定理、泰勒定理;掌握求函数的 极值,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的方法;求方程近似解的二分 法和切线法;能用导数描述一些经济学中的问题,会应用拉格朗日定理,能描绘函数的图形,会 解简单的最大值和最小值问题。 3.教学重点难点: 掌握函数的极值的计算方法,判断函数的增减性与函数图形的凹凸性,求函数图形的拐点的 方法。熟悉函数图形的描绘。难点为柯西定理、泰勒定理;函数作图。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习。 第四章 不定积分 1.基本内容: 不定积分的概念,性质,基本积分公式,换元积分法,分部积分法,有理函数、三角函数, 有理函数及简单的无理函数的积分举例。 2.教学基本要求: 理解不定积分的概念和性质,掌握基本积分公式,换元积分法,分部积分法;了解有理函数 的积分,可化为有理函数的积分。 3.教学重点难点: 不定积分的概念,性质,基本积分公式,换元积分法,分部积分法。第二类换元积分法,有 理函数积分法。 4.教学建议:采用讲授法、提问法、课堂讨论法开展本章课程的学习
四、教学环节与学时分配 课外辅 序号 教学内容 总学 备 果外到 第一章函数、极限、连续 18 160 2第二章导数与微分 1210002 0 “其它” 主要方式 3 第三章 中值定理与导数的应用 14 12 为习题课 4第四章不定积分 108002 0 5机动(阶段复习备用) 2 00020 共计 564600100 五、教学中应注意的问题: 通过教学要实现传授知识和发展能力两方面的教学目的,能力培养要贯穿教学全过程。教学 中注意满足不同层次学生的不同要求,积极为学生终身学习搭建平台、拓展空间。不仅把数学课 程当作重要的基础课和工具课,更将其视为一门素质课。教学中要结合教学内容及学生特点,选 择适宜的教学方法与教学手段,突出重点、化解难点,有意识、有目的、有重点地营造有利于学 生能力发展的氛围,启发学生思维,促进学生能力的提高。并通过教研活动统一教学行为。 六、实验/实践内容:无 七、考核方式: 考试采用闭卷考试形式。内容包括基本概念,基础理论,分析计算,题型分为填空、选择、 计算或解答题,证明等方式,题目的难易程度要视学生的实际情况而定。· 总评成绩:平时学习过程的考核占30%,理论闭卷考试成绩占70%,其中平时学习过程包 括平时作业(占总成绩的20%),考勤(占总成绩的5%),课堂表现及课后互动(占总成绩的5%)。 八、教材及主要参考书: 1、选用教材 《高等数学》(上下册)廖新元等编,复旦大学出版社,2012年。 2、主要参考书: 山《微积分》上下册吴赣吕主编,中国人民大学出版社,2009。口 2]《高等数学》(上下册,第六版)同济大学主编,高等教有出版社,2007年。 3)】《数学复习指南》,陈文灯等编,世界图书出版社,2010年。 九、教改说明及其他 执笔人:刘小佑 系室审核人:廖茂 4
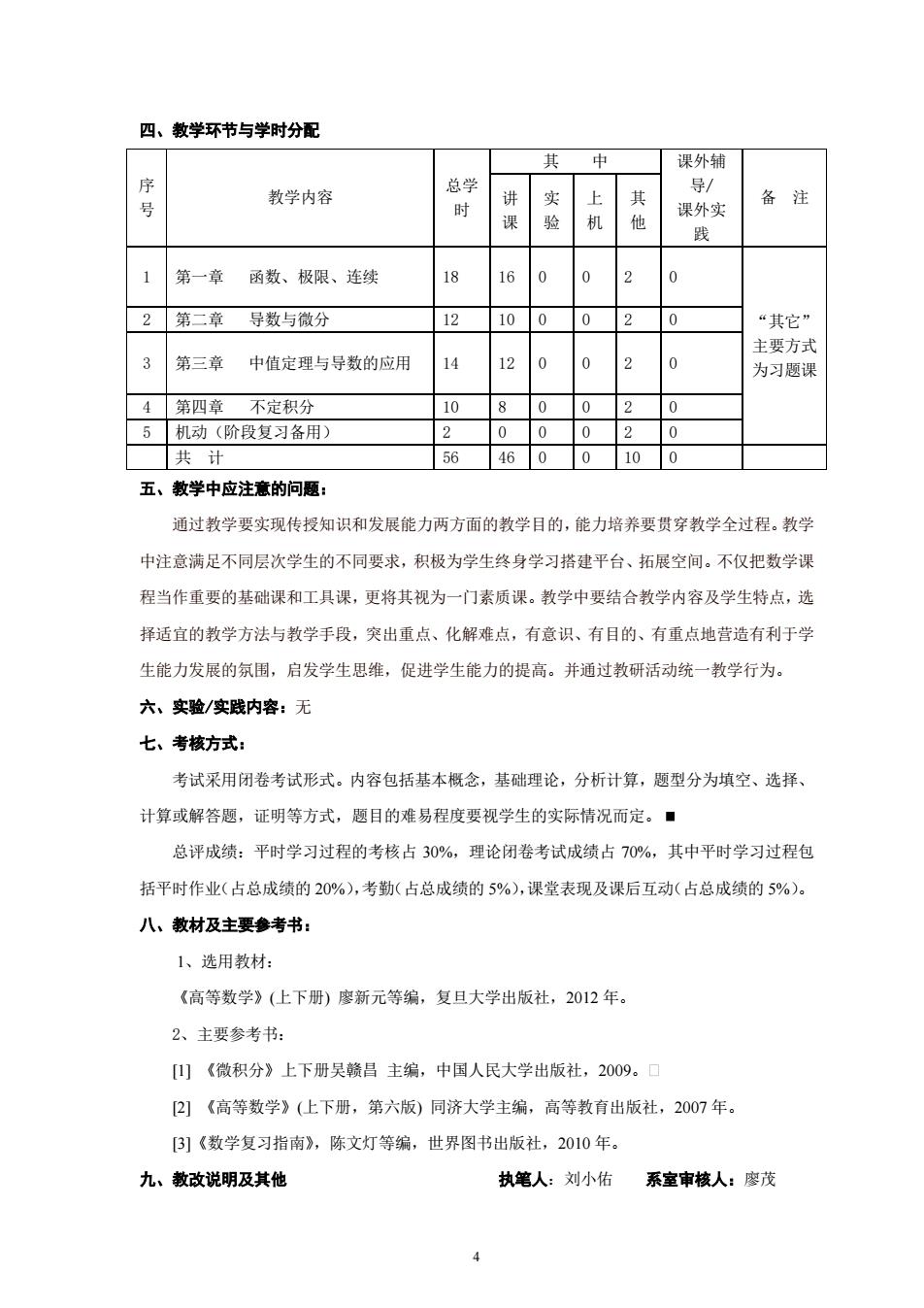
4 四、教学环节与学时分配 序 号 教学内容 总学 时 其 中 课外辅 导/ 课外实 践 讲 备 注 课 实 验 上 机 其 他 1 第一章 函数、极限、连续 18 16 0 0 2 0 “其它” 主要方式 为习题课 2 第二章 导数与微分 12 10 0 0 2 0 3 第三章 中值定理与导数的应用 14 12 0 0 2 0 4 第四章 不定积分 10 8 0 0 2 0 5 机动(阶段复习备用) 2 0 0 0 2 0 共 计 56 46 0 0 10 0 五、教学中应注意的问题: 通过教学要实现传授知识和发展能力两方面的教学目的,能力培养要贯穿教学全过程。教学 中注意满足不同层次学生的不同要求,积极为学生终身学习搭建平台、拓展空间。不仅把数学课 程当作重要的基础课和工具课,更将其视为一门素质课。教学中要结合教学内容及学生特点,选 择适宜的教学方法与教学手段,突出重点、化解难点,有意识、有目的、有重点地营造有利于学 生能力发展的氛围,启发学生思维,促进学生能力的提高。并通过教研活动统一教学行为。 六、实验/实践内容:无 七、考核方式: 考试采用闭卷考试形式。内容包括基本概念,基础理论,分析计算,题型分为填空、选择、 计算或解答题,证明等方式,题目的难易程度要视学生的实际情况而定。 总评成绩:平时学习过程的考核占 30%,理论闭卷考试成绩占 70%,其中平时学习过程包 括平时作业(占总成绩的 20%),考勤(占总成绩的 5%),课堂表现及课后互动(占总成绩的 5%)。 八、教材及主要参考书: 1、选用教材: 《高等数学》(上下册) 廖新元等编,复旦大学出版社,2012 年。 2、主要参考书: [1] 《微积分》上下册吴赣昌 主编,中国人民大学出版社,2009。 [2] 《高等数学》(上下册,第六版) 同济大学主编,高等教育出版社,2007 年。 [3]《数学复习指南》,陈文灯等编,世界图书出版社,2010 年。 九、教改说明及其他 执笔人:刘小佑 系室审核人:廖茂

《高等数学B1》课程考试大纲 课程编号:130704005 总学时数:56学时 学分:3.5学分 一、考试对像 经济管理类专业。 二、考试目的 本课程考试目的是对学生系统获得一元函数微积分的基木知识,基础理论和常用的运算方 法,比较熟练的运算能力、抽象思维能力、逻辑推理能力和效果检验,以便使学生自我发现哪些 知识学得好,哪些还需要更进一步加强,为学习后继课程和进一步扩大数学知识奠定必要的数学 基础。 三、考试要求 1.试题覆盖面要广,既要注意覆盖基础知识和基本技能的掌握程度,同时也要考虑有 定的区分度。 2.试题难度要适中,要考核学生对基础知识和基本技能的掌握程度,避免过难过偏,考试 结果要能反映大多数学生的实际水平。 3.试趣要重视对后继课程学习有所帮助。 4.试题要体现应用性,要有一定量的应用题。 四、考试内容与要求 第一章函数与极限20~30分值 1、考试内容:函数概念、函数的几种特性,反函数、复合函数和初等函数。极限、极限概 念,左右极限,无穷小量,无穷大量,极限的四则运算,两个极限存在准则,两个重要极限,无 穷小的比较。连续性、连续性概念,连续函数的运算性质,基本初等函数和初等函数的连续性, 闭区间上连续函数的性质(最大值,最小值定理和介值定理)。 2、考试要求:理解函数的概念,函数在一点连续的概念:熟悉基本初等函数的性质及其图 形:理解复合函数概念,两个极限存在准则,无穷小、无穷大概念,初等函数的连续性:掌握极 限四则运算法则及无穷小的比较:会用两个重要极限求极限,会判断间断点的类型:能应用最大 值,最小值定理和介值定理来解题。 第二章导数与微分25一30分值
5 《高等数学 B1》课程考试大纲 课程编号:130704005 总学时数:56 学时 学分:3.5 学分 一、考试对象 经济管理类专业。 二、考试目的 本课程考试目的是对学生系统获得一元函数微积分的基本知识,基础理论和常用的运算方 法,比较熟练的运算能力、抽象思维能力、逻辑推理能力和效果检验,以便使学生自我发现哪些 知识学得好,哪些还需要更进一步加强,为学习后继课程和进一步扩大数学知识奠定必要的数学 基础。 三、考试要求 1. 试题覆盖面要广,既要注意覆盖基础知识和基本技能的掌握程度,同时也要考虑有一 定的区分度。 2. 试题难度要适中,要考核学生对基础知识和基本技能的掌握程度,避免过难过偏,考试 结果要能反映大多数学生的实际水平。 3. 试题要重视对后继课程学习有所帮助。 4. 试题要体现应用性,要有一定量的应用题。 四、考试内容与要求 第一章 函数与极限 20~30 分值 1、考试内容:函数概念、函数的几种特性,反函数、复合函数和初等函数。极限、极限概 念,左右极限,无穷小量,无穷大量,极限的四则运算,两个极限存在准则,两个重要极限,无 穷小的比较。连续性、连续性概念,连续函数的运算性质,基本初等函数和初等函数的连续性, 闭区间上连续函数的性质(最大值,最小值定理和介值定理)。 2、考试要求 :理解函数的概念,函数在一点连续的概念;熟悉基本初等函数的性质及其图 形;理解复合函数概念,两个极限存在准则,无穷小、无穷大概念,初等函数的连续性;掌握极 限四则运算法则及无穷小的比较;会用两个重要极限求极限,会判断间断点的类型;能应用最大 值,最小值定理和介值定理来解题。 第二章 导数与微分 25~30 分值

1、考试内容:导数概念,导数的几何意义,可导性与连续性之间的关系,导数的运算法则, 基本初等函数的导数公式,高阶导数,隐函数的导数,对数求导法,由参数方程所确定的函数的 导数,微分概念及其运算法则。 2、考试要求:理解导数和微分概念。熟悉导数和微分的运算法则和导数的基本公式,熟练 地求初等函数、隐函数和参数式所确定的函数的一阶、二阶导数。 第三章微分中值定理与导数的应用20~25分值 1、考试内容:中值定理及应用:罗必达法则,函数增减性判定法,函数的极值及其求法, 最大值,最小值问题,函数图形的凹凸及其判定法,拐点及其求法,水平与垂直渐近线的求法。 2、考试要求:理解罗尔定理,拉格朗日定理和函数的极值概念。掌握函数的极值求法,会 判断函数的增减性与函数图形的凹凸性和函数图形的拐点及水平与垂直渐近线的求法。会解简 单的求最大值和最小值问题。 第四章不定积分1525分值 1、考试内容:不定积分的概念,性质,基本积分公式,换元积分法,分部积分法,有理函 数、三角函数,有理函数及简单的无理函数的积分举例。 2、考试要求:理解不定积分和定积分的概念和性质。会利用基本积分公式及换元积分法, 分部积分法公式求积分。 五、考试方式及时间 考试采用闭卷考试形式,考试时间为100分钟。内容包括基本概念,基础理论,分析计算, 题型分为填空、选择、计算或解答题,证明等方式,题目的难易程度要视学生的实际情况而定。 ·六、考试题型结构及分值分布 填空题:20%选择题20%计算12~15% 解答:35~42%证明题:6一10%。 七、成绩综合评定办法 学生最后总成绩由平时+理论闭卷考试成绩的总和确定。 总评成绩:平时学习过程的考核占30%,理论闭卷考试成绩占70%,其中平时学习过程包 括平时作业(占总成绩的20%),考勒(占总成绩的5%),课堂表现及课后互动(占总成绩的5%)。 八、教材及主要参考书 1、选用教材: 《高等数学》(上下册)廖新元等编,复旦大学出版社,2012年。 2、主要参考书: 6
6 1、考试内容:导数概念,导数的几何意义,可导性与连续性之间的关系,导数的运算法则, 基本初等函数的导数公式,高阶导数,隐函数的导数,对数求导法,由参数方程所确定的函数的 导数,微分概念及其运算法则。 2、考试要求 :理解导数和微分概念。熟悉导数和微分的运算法则和导数的基本公式,熟练 地求初等函数、隐函数和参数式所确定的函数的一阶、二阶导数。 第三章 微分中值定理与导数的应用 20~25 分值 1、考试内容:中值定理及应用;罗必达法则,函数增减性判定法,函数的极值及其求法, 最大值,最小值问题,函数图形的凹凸及其判定法,拐点及其求法,水平与垂直渐近线的求法。 2、考试要求 :理解罗尔定理,拉格朗日定理和函数的极值概念。掌握函数的极值求法,会 判断函数的增减性与函数图形的凹凸性和函数图形的拐点及水平与垂直渐近线的求法。会解简 单的求最大值和最小值问题。 第四章 不定积分 15~25 分值 1、考试内容:不定积分的概念,性质,基本积分公式,换元积分法,分部积分法,有理函 数、三角函数,有理函数及简单的无理函数的积分举例。 2、考试要求 :理解不定积分和定积分的概念和性质。会利用基本积分公式及换元积分法, 分部积分法公式求积分。 五、考试方式及时间 考试采用闭卷考试形式,考试时间为 100 分钟。内容包括基本概念,基础理论,分析计算, 题型分为填空、选择、计算或解答题,证明等方式,题目的难易程度要视学生的实际情况而定。 六、考试题型结构及分值分布 填空题:20% 选择题 20% 计算 12~15% 解答:35~42% 证明题: 6~10%。 七、成绩综合评定办法 学生最后总成绩由平时+理论闭卷考试成绩的总和确定。 总评成绩:平时学习过程的考核占 30%,理论闭卷考试成绩占 70%,其中平时学习过程包 括平时作业(占总成绩的 20%),考勤(占总成绩的 5%),课堂表现及课后互动(占总成绩的 5%)。 八、教材及主要参考书 1、选用教材: 《高等数学》(上下册) 廖新元等编,复旦大学出版社,2012 年。 2、主要参考书:

)《微积分》上下册吴赣昌主编,中国人民大学出版社,2009。口 [2]《高等数学》(上下册,第六版)同济大学主编,高等教有出版社,2007年。 B)《数学复习指南》,陈文灯等编,世界图书出版社,2010年。 执笔人:刘小佑系室审核人:廖茂新
7 [1] 《微积分》上下册吴赣昌 主编,中国人民大学出版社,2009。 [2] 《高等数学》(上下册,第六版) 同济大学主编,高等教育出版社,2007 年。 [3]《数学复习指南》,陈文灯等编,世界图书出版社,2010 年。 执笔人:刘小佑 系室审核人:廖茂新