新疆大学：《混凝土结构设计原理》课程教学资源（课件讲稿）第6章 受压构件 Compressive Element or Column（6.4 矩形截面正截面承载力计算 6.5 工形截面正截面承载力计算 6.6 双向偏心受压构件的正截面承载力计算）

第六章受压构件 6.4矩形截面正截面承载力计算 一、不对称配筋截面设计 1、大偏心受压（受拉破坏） 己知：截面尺寸（仍×）、材料强度(f、f,v)人、构件长细比 (L,)以及轴力N和弯矩M设计值， 若e>eh.min-0.3ho, 一 般可先按大偏心受压情况计算 N=N=af bx+fA-fA N-e≤a4hh-+f,4所-a) e=e+0.5h-a FAs fA's 8.4矩形截面正截面承载力计算

第六章 受压构件 8.4 矩形截面正截面承载力计算 6.4 矩形截面正截面承载力计算 一、不对称配筋截面设计 1、大偏心受压（受拉破坏） 已知：截面尺寸(b×h)、材料强度( fc、fy，f'y )、构件长细比 (l0 /h)以及轴力N和弯矩M设计值， 若ei>eib.min =0.3h0， 一般可先按大偏心受压情况计算 u c y s y As N  N f bx  f A  f e e h a    i 0.5 ) ( ) 2 ( 0 f A h0 a x N e f c bx h y s         fyAs f'yA' s N e ei

第六章受压构件 N=N=agf bx+fyA-fy A. (I)A和A'均未知时 Ne≤cfbx(h,- +SA(k-a) 两个基本方程中有三个未知数，A、A'和x,故无唯一解。 与双筋梁类似，为使总配筋面积(A,+A)最小？ 可取x=5h得 ★若A、<0.002bh? A Ne-of bh65(1-0.556 则取A'g=0.002bh,然后按 f(ho-a') A'为已知情况计算。 of bhos,+fA-N ★若A,<Pminbh? A 应取A,=Pminbh

⑴As和A's均未知时 ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s u c y s y s                 两个基本方程中有三个未知数，As、A's和 x，故无唯一解。 与双筋梁类似，为使总配筋面积（As+A's）最小? 可取x=xbh0得 ( ) (1 0.5 ) 0 2 0 f h a Ne f bh A y c b b s         x x ★ 若A's<0.002bh? 则取A's=0.002bh，然后按 A's为已知情况计算。 y c b y s s f f bh f A N A       0 x ★ 若As <rminbh ? 应取As =rminbh。 第六章 受压构件

第六章受压构件 N=N =af bx+fA-fyA. (2)A'为已知时 Nesb(h克+f4-a 当A'、已知时，两个基本方程有二个未知数A、和x,有唯一解。 先由第二式求解x,若x2a',则可将代入第一式得 of bx+fA-N ★若A,若小于Ominbh? 应取A,=Pminbho fA: OA's

⑵A's为已知时 ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s u c y s y s                 当A's已知时，两个基本方程有二个未知数As 和 x，有唯一解。 先由第二式求解x，若x 2a'，则可将代入第一式得 y c y s s f f bx f A N A       ★ 若As若小于rminbh？ 应取As =rminbh。 第六章 受压构件 fyAs s' sA's N ei

第六章受压构件 N=N=af bx+fA-fA. (2)A'为已知时 Ne≤adbm-2+f,4gh,-a) 当A'、已知时，两个基本方程有二个未知数A、和x,有唯一解。 先由第二式求解x,若x2a',则可将代入第一式得 af bx+fA-N ★若A,若小于Ominbh? f, 应取Ag=Pminbh。 若x>,？则应按A为未知情况重新计算确定A' 若x<2a'?则可偏于安全的近似取x=2a',按下式确定A

⑵A's为已知时 ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s u c y s y s                 当A's已知时，两个基本方程有二个未知数As 和 x，有唯一解。 先由第二式求解x，若x 2a'，则可将代入第一式得 y c y s s f f bx f A N A       若x > xbh0？ ★ 若As若小于rminbh？ 应取As =rminbh。 则应按A's为未知情况重新计算确定A's 若x<2a' ？ 则可偏于安全的近似取x=2a'，按下式确定As 第六章 受压构件

第六章受压构件 N=Nu=bx+fA-∫，A, (2)A'、为已知时 Ne≤对bxh-2+f4h,-a) 当A'、已知时，两个基本方程有二个未知数A、和x,有唯一解。 先由第二式求解x,若x2a',则可将代入第一式得 af bx+fA-N ★若A,若小于Ominbh? fy 应取A,=Pminbh。 若x>5,？则应按A'、为未知情况重新计算确定A'、 若x<2a'? 则可偏于安全的近似取=2'，按下式确定A N(e-0.5h+a) ★若A,若小于Pnibh? A f,(ho-a') 应取A,=Pminbh

⑵A's为已知时 ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s u c y s y s                 当A's已知时，两个基本方程有二个未知数As 和 x，有唯一解。 先由第二式求解x，若x 2a'，则可将代入第一式得 y c y s s f f bx f A N A       若x > xbh0？ 0 ( 0.5 ) ( ) i s y N e h a A f h a       ★ 若As若小于rminbh？ 应取As =rminbh。 则应按A's为未知情况重新计算确定A's 若x<2a' ？ 则可偏于安全的近似取x=2a'，按下式确定As 第六章 受压构件 ★若As若小于rminbh？ 应取As =rminbh

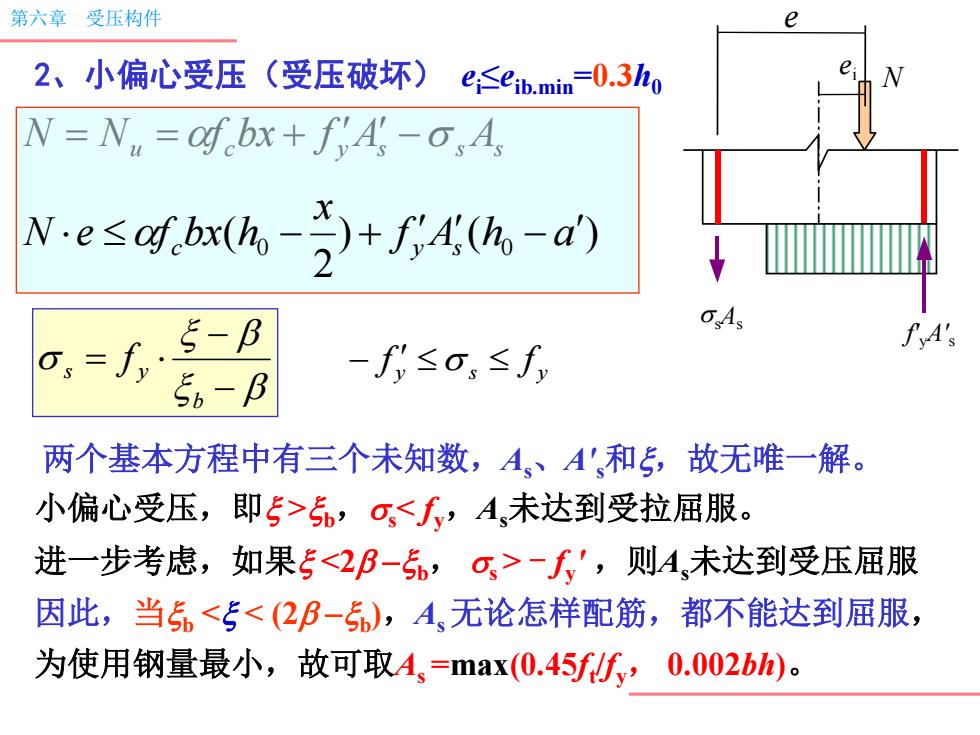
第六章受压构件 e 2、小偏心受压（受压破坏)e≤eh.min-0.3h0 N=N=af bx+fA-s A Ne≤c4fbxh-习+f4h-a) ,=f,。-B ,5-B -f≤o,≤f 两个基本方程中有三个未知数，A、A'和5，故无唯一解。 小偏心受压，即>5，¤-∫'，则4，未达到受压屈服 因此，当5<5<(2B-5),A无论怎样配筋，都不能达到屈服， 为使用钢量最小，故可取A、=max(0.45f5, 0.002bh)

2、小偏心受压（受压破坏） ei≤eib.min =0.3h0 u c y As s As N  N f bx  f   s x  x  s     b s y f y s y  f  s  f 两个基本方程中有三个未知数，As、A's和x，故无唯一解。 小偏心受压，即x >xb，ss - fy ' ，则As未达到受压屈服 因此，当xb <x < (2 xb )，As 无论怎样配筋，都不能达到屈服， 为使用钢量最小，故可取As =max(0.45ft /fy， 0.002bh)。 ) ( ) 2 ( 0 f A h0 a x N e f c bx h y s         第六章 受压构件 ssAs f'yA' s N ei e

第六章受压构件 ◆另一方面，当偏心距很小时，如果附 加偏心距ea与荷载偏心距e方向相反， ◆则可能发生A.一侧混凝土首先达到受 压破坏的情况。 ◆此时通常为全截面受压，由图示截面 应力分布，对A'取矩，可得， fyAs fyA's Ne'-fbh(ho-0.5h) A、= f(%6-a) 0.451 f, e'=0.5h-d-(eo-ea), A、=max0.002bh ho-h-a Ne'-fbh(h-0.5h) (h -a)

◆ 另一方面，当偏心距很小时，如果附 加偏心距ea与荷载偏心距e0方向相反， ◆ 则可能发生As一侧混凝土首先达到受 压破坏的情况。 ◆ 此时通常为全截面受压，由图示截面 应力分布，对A's取矩，可得， f'y A' s N e0 - ea e' f'y As ( ) ( 0.5 ) 0 0 f h a Ne f bh h h A y c s        e'=0.5h-a'-(e0-ea ), h' 0 =h-a'                  ( ) ( 0.5 ) 0.002 0.45 max 0 0 f h a Ne f bh h h bh f f A y c y t s 第六章 受压构件

第六章受压构件 确定A,后，就只有5和A'、两个未 =从.时加+-大月 知数，故可得唯一解。 根据求得的5，可分为三种情况 Ne≤对bxh,-7+f4h,-a) (1)若5(2B-5),o=',基本公式转化为下式， N=N =afbx+fA+fAs 重新求解5和A'、 Ne≤afbx(h-+fA(h-a) (3)若5hn>h,应取x=h,同时应取a=l,代入基本公式直接解得A' Ne-fbh(ho-0.5h) f(h-a')

确定As后，就只有x 和A's两个未 知数，故可得唯一解。 根据求得的x ，可分为三种情况 ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s s b u c y s y                   x  x   ⑴若x (2 xb )，ss= -fy '，基本公式转化为下式， ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s u c y s y s                  ⑶若x h0>h，应取x=h，同时应取 =1，代入基本公式直接解得A's ( ) ( 0.5 ) 0 0 f h a Ne f bh h h A y c s        重新求解x 和A's 第六章 受压构件

第六章 受压构件 由基本公式求解5和A',的具体运 N-N.-cbx+-5-d 56-B 算是很麻烦的。 迭代计算方法 N.esafbx(h-(h-a) 用相对受压区高度5， N·e≤bh5(1-0.55)+fA(h-d) 在小偏压范围5=5~1.1，a=1-0.5)变化很小。 0.6 对于Ⅱ级钢筋和 0.4 <C50混凝土，a,在 0.40.5之间，近似 0.2 取0.45 0 0 0.2 0.4 0.6 0.8 1

由基本公式求解x 和A's的具体运 算是很麻烦的。 迭代计算方法 用相对受压区高度x ， (1 0.5 ) ( ) 0 2 N e f c bh0 x  x  f y As  h  a  在小偏压范围x =xb~1.1， 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 对于Ⅱ级钢筋和 <C50混凝土，s在 0.4~0.5之间，近似 取0.45 s =x(1-0.5x) 变化很小。 ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s s b u c y s y                   x  x   第六章 受压构件

第六章受压构件 取a=0.45 -o如+-5会 N.e≤ad.bxh-习+f4h-a） Ne-0.45cgf bhi f(ho-a') N.esafbhs(1-0.55)+fA(ho-a) A'四的误差最大约为12%。 - 如需进一步求较为精确的解，可 将A'、四代入基本公式求得5， dbi。-fA月 试分析证明上述迭代是 4(2) Ne-cgbh65(1-0.550） 收敛的，且收敛速度很 f(h-a') 快

( ) 0.45 0 2 (1) 0 f h a Ne f bh A y c s        A's (1)的误差最大约为12%。 如需进一步求较为精确的解，可 将A's (1)代入基本公式求得x， x   x   x         b c y s s b y s y f bh f A N f A f A 1 0 (1) (1) ( ) (1 0.5 ) 0 2 (1) (1) (2) 0 f h a Ne f bh A y c s         x x 取s =0.45 试分析证明上述迭代是 收敛的，且收敛速度很 快。 ) ( ) 2 ( 0 f A h0 a x N e f bx h N N f bx f A f A c y s s b u c y s y                   x  x   (1 0.5 ) ( ) 0 2 N e f c bh0 x  x  f y As  h  a  第六章 受压构件