结构力学一第五章静定平面桁架结构和组合结构 而海南大学士木建筑工程学院 第五章静定平面桁架和组合结构 第一节概述 桁架是土木工程中广泛采用的结构形式之一。 (a)钢筋混凝土屋架 (b)钢屋架
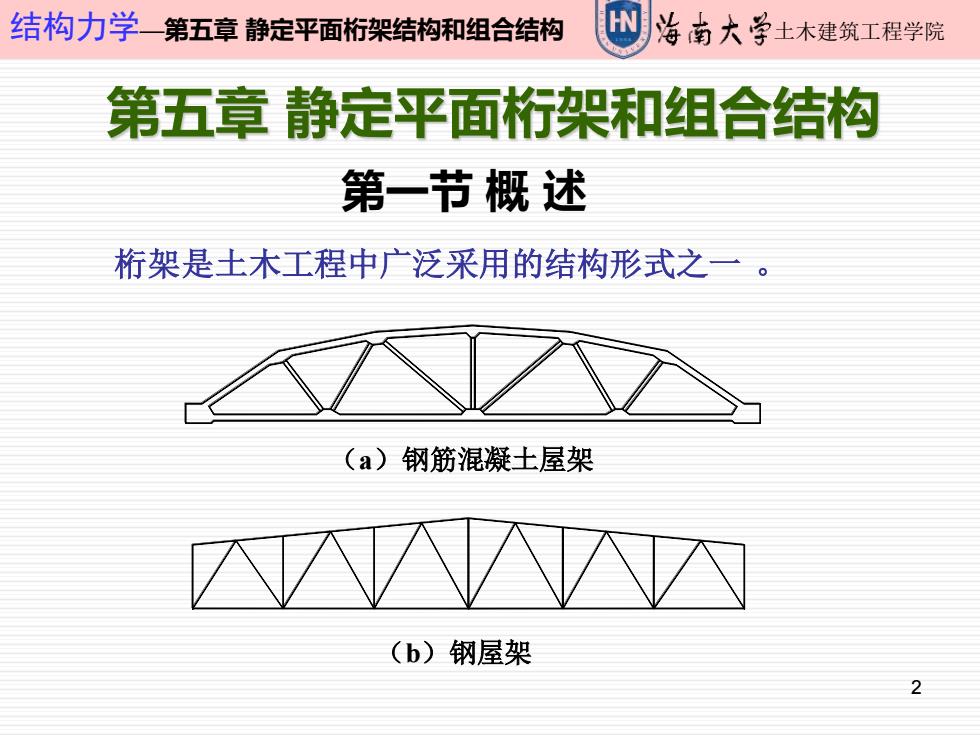
2 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 第五章 静定平面桁架和组合结构 桁架是土木工程中广泛采用的结构形式之一 。 (a)钢筋混凝土屋架 (b)钢屋架 第一节 概 述
结构力学一第五章静定平面桁架结构和组合结构 海南大学土木建筑工程学院 (c)钢天窗架 桁架一一是由若干直杆构成的,所有杆件的两端均用铰联接。 静定桁架 平面桁架 超静定桁架 空间桁架 静定平面桁架 一一所有杆件的轴线以及外力的作用线都位于 同一平面内的无多余约束的桁架结构。 本章只讨论静定平面桁架 3
3 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 桁架——是由若干直杆构成的,所有杆件的两端均用铰联接。 静定桁架 超静定桁架 平面桁架 空间桁架 静定平面桁架——所有杆件的轴线以及外力的作用线都位于 同一平面内的无多余约束的桁架结构。 (c)钢天窗架 本章只讨论静定平面桁架

结构力学一第五章静定平面桁架结构和组合结构 海南大学土木建筑工程学院 桁架的计算简图 桁架的计算简图往往都是理想化的桁架,称为理 想桁架。应符合以下假设: (1)各杆的两端用理想铰(绝对光滑而无摩擦)相互 联结: (2)各杆的轴线都是绝对平直而且在同一平面内并通 过铰的几何中心; (3)荷载和支座反力都作用在结点上并位于桁架的平 面内。 理想桁架的各杆均为两端铰结的直杆,仅在两端受 约束力作用,只承受轴向力,因此桁架各杆均为二力杆。 4
4 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 一、桁架的计算简图 (3)荷载和支座反力都作用在结点上并位于桁架的平 面内。 (1)各杆的两端用理想铰(绝对光滑而无摩擦)相互 联结; (2)各杆的轴线都是绝对平直而且在同一平面内并通 过铰的几何中心; 桁架的计算简图往往都是理想化的桁架,称为理 想桁架。应符合以下假设: 理想桁架的各杆均为两端铰结的直杆,仅在两端受 约束力作用,只承受轴向力,因此桁架各杆均为二力杆
结构力学—第五章静定平面桁架结构和组合结构 W 海南大学土木建筑工程学院 上弦杆 竖杆 结点 腹杆 斜杆 结间长度 下弦杆 跨度 钢筋混凝土屋架计算简图 简图与实际的偏差:并非理想较接,并非理想直杆, 并非只有结点荷载。 主内力:按计算简图计算出的内力。 次内力:实际内力与主内力的差值。 5
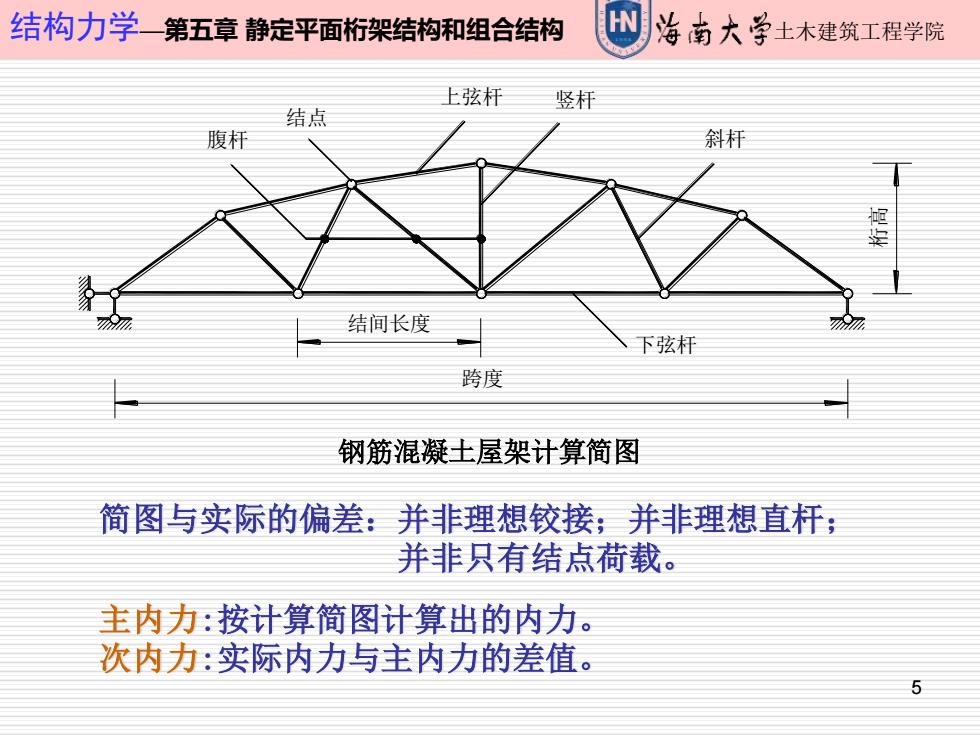
5 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 钢筋混凝土屋架计算简图 桁高 上弦杆 跨度 结间长度 下弦杆 竖杆 腹杆 斜杆 结点 主内力:按计算简图计算出的内力。 次内力:实际内力与主内力的差值。 简图与实际的偏差:并非理想铰接;并非理想直杆; 并非只有结点荷载
结构力学一第五章静定平面桁架结构和组合结构 四治南大学土木建筑工程学院 三、平面桁架的分类 1.按几何组成分类 简单桁架:在基础或一个铰结三角形上依次加二元体构成 联合桁架:由简单桁架按基本组成规则构成 复杂桁架:非上述两种方式组成的其它桁架 联合桁架 单 架 联合桁架 复杂桁架 6
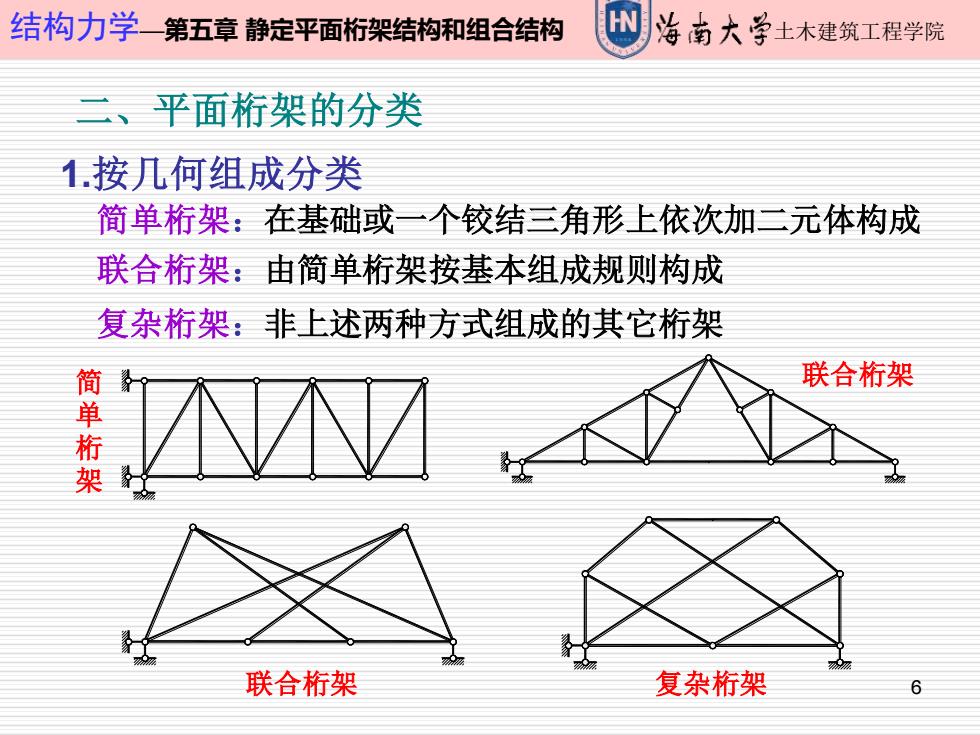
6 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 二、平面桁架的分类 1.按几何组成分类 联合桁架:由简单桁架按基本组成规则构成 简单桁架:在基础或一个铰结三角形上依次加二元体构成 复杂桁架:非上述两种方式组成的其它桁架 简 单 桁 架 联合桁架 联合桁架 复杂桁架
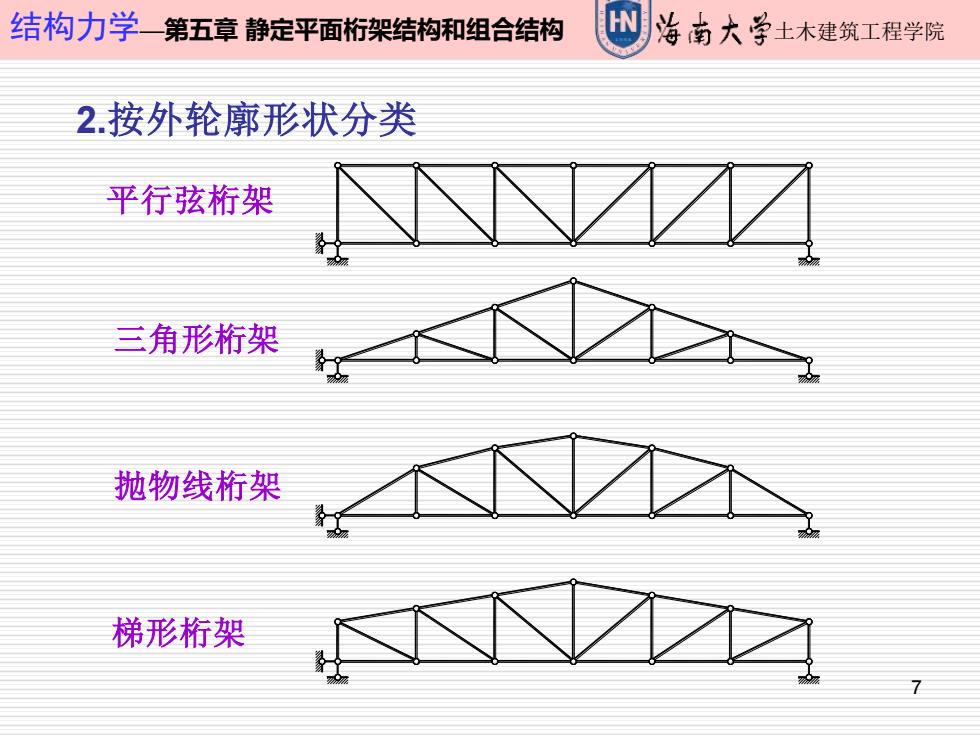
结构力学一第五章静定平面桁架结构和组合结构 海南大学土木建筑工程学院 2.按外轮廓形状分类 平行弦桁架 三角形桁架 抛物线桁架 梯形桁架
7 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 2.按外轮廓形状分类 梯形桁架 平行弦桁架 三角形桁架 抛物线桁架

结构力学一第五章静定平面桁架结构和组合结构 W 洛南大学上木建筑工程学院 第二节静定平面桁架 桁架内力就是指桁架各杆的轴力,规定以受拉为正, 受压为负。 结点法 桁架内力计算的方法有: 截面法 二者的联合应用 、结点法 结点法是截取桁架的一个结点为隔离体,利用结点的 静力平衡条件求解桁架杆件内力的方法。 桁架任一结点上所受的各力构成一平面汇交力系,所 以可对每一结点列出两个平衡方程进行求解。 8
8 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 桁架内力就是指桁架各杆的轴力,规定以受拉为正, 受压为负。 第二节 静定平面桁架 桁架内力计算的方法有: 结点法 截面法 二者的联合应用 桁架任一结点上所受的各力构成一平面汇交力系,所 以可对每一结点列出两个平衡方程进行求解。 结点法是截取桁架的一个结点为隔离体,利用结点的 静力平衡条件求解桁架杆件内力的方法。 一、结点法
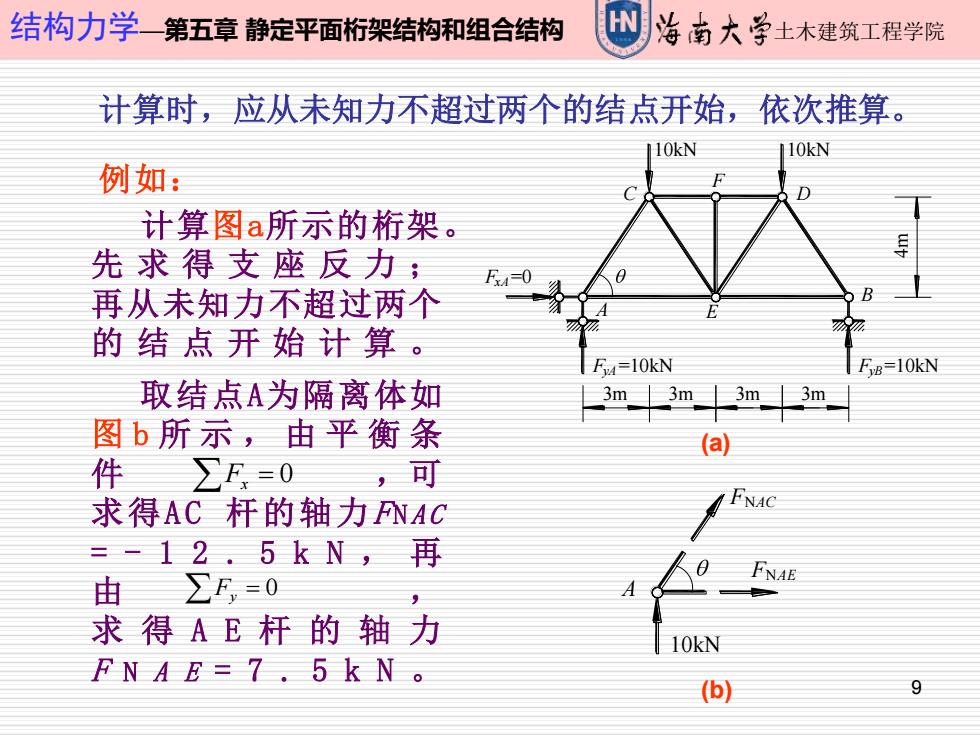
结构力学一第五章静定平面桁架结构和组合结构 W 海南大学士木建筑工程学院 计算时,应从未知力不超过两个的结点开始,依次推算。 10kN 10kN 例如 D 计算图a所示的桁架。 先求得支座反力; F4=0 再从未知力不超过两个 B 的结点开始计算。 F4=10kN FB=10kN 取结点A为隔离体如 3m3m 3m 3m 图b所示,由平衡条 (a 件 ∑E=0 ,可 求得AC杆的轴力PNAC =-12.5kN,再 由∑E,=0 FNAE 求得AE杆的轴力 10kN FNAE=7.5kN。 (b 9
9 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 (a) (b) 计算时,应从未知力不超过两个的结点开始,依次推算。 A C F D B E 3m 3m 3m 3m 4m 10kN 10kN FyA =10kN FxA =0 FyB =10kN 计算图a所示的桁架。 先 求 得 支 座 反 力 ; 再从未知力不超过两个 的 结 点 开 始 计 算 。 A 10kN FNAC FNAE 例如: 取结点A为隔离体如 图 b 所 示 , 由平衡条 件 ,可 求得A C 杆的轴力F N A C = - 1 2 . 5 k N , 再 由 , 求 得 A E 杆的轴力 F N A E = 7 . 5 k N 。 Fy = 0 Fx = 0
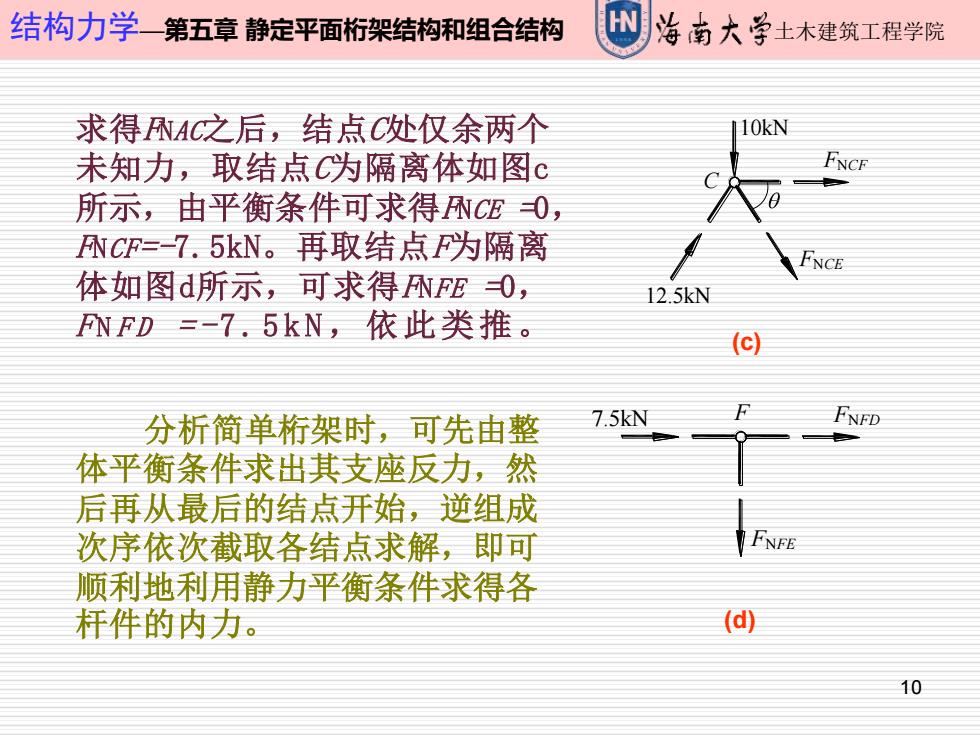
结构力学_第五章静定平面桁架结构和组合结构 海南大学土木建筑工程学院 求得NAC之后,结点C改处仅余两个 10kN 未知力,取结点C为隔离体如图c FNCF 所示,由平衡条件可求得NCEO, NCF=7.5kN。再取结点F为隔离 FNCE 体如图d所示,可求得NFEO, 12.5kN ANFD=-7,5kN,依此类推。 (c) 分析简单桁架时,可先由整 7.5kN FNFD 体平衡条件求出其支座反力,然 后再从最后的结点开始,逆组成 次序依次截取各结点求解,即可 FNFE 顺利地利用静力平衡条件求得各 杆件的内力。 d 10
10 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 求得FNAC之后,结点C处仅余两个 未知力,取结点C为隔离体如图c 所示,由平衡条件可求得FNCE =0, FNCF=-7.5kN。再取结点F为隔离 体如图d所示,可求得FNFE =0, F N F D = - 7 . 5 k N ,依此类推。 (c) (d) C 10kN FNCF FNCE 12.5kN F FNFD FNFE 分析简单桁架时,可先由整 7.5kN 体平衡条件求出其支座反力,然 后再从最后的结点开始,逆组成 次序依次截取各结点求解,即可 顺利地利用静力平衡条件求得各 杆件的内力
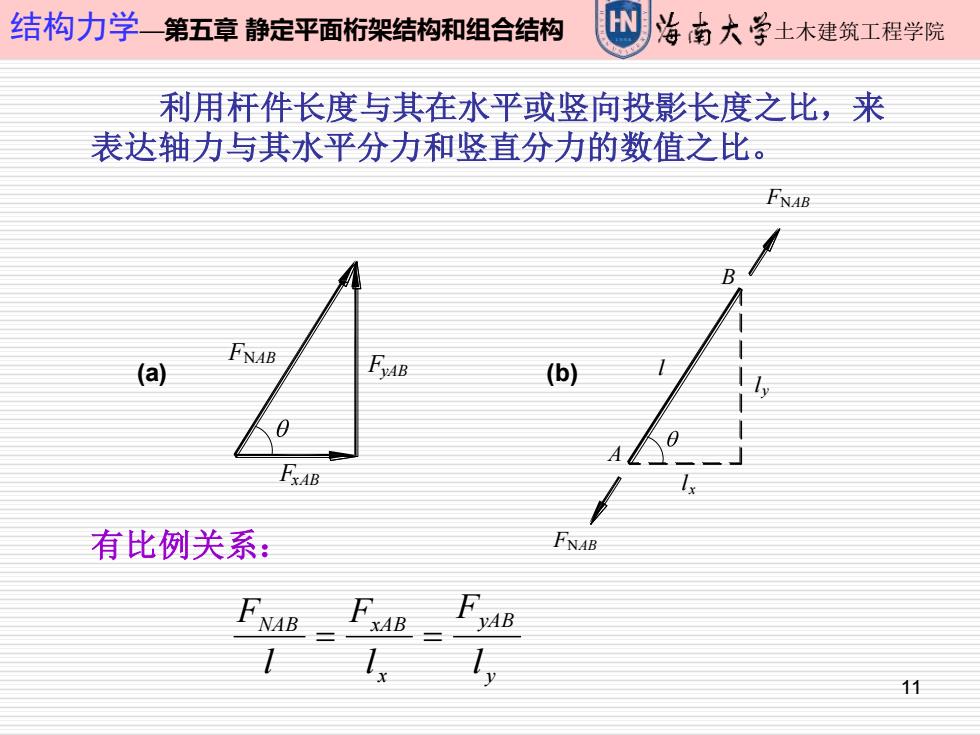
结构力学—第五章静定平面桁架结构和组合结构 W 治南大学上木建筑工程学院 利用杆件长度与其在水平或竖向投影长度之比,来 表达轴力与其水平分力和竖直分力的数值之比。 fNaB B fNaB (a) (b) FxAB 有比例关系: FNAB 11
11 结构力学—第五章 静定平面桁架结构和组合结构 土木建筑工程学院 利用杆件长度与其在水平或竖向投影长度之比,来 表达轴力与其水平分力和竖直分力的数值之比。 (a) (b) FNAB FyAB FxAB FNAB l x FNAB l l y A B y yAB x NAB xAB l F l F l F = = 有比例关系: