
结构力学一—第九章力矩分配法与近似法 海南大学土木建筑工程学院 第九章力矩分配法与近似法 第一节力矩分配法的基本概念 力矩分配法一一是直接从实际结构的受力和变形状态出 发,根据位移法基本原理,从开始建立 的近似状态,逐步通过增量调整修正, 最后收敛于真实状态的渐近法。 力矩分配法计算过程简单直观,主要应用于分析连 续梁和无结点线位移的刚架。 分析中杆端转角、杆端弯矩以及固端弯矩的正负号 规定与位移法相同。 2
2 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 第一节 力矩分配法的基本概念 第九章 力矩分配法与近似法 力矩分配法——是直接从实际结构的受力和变形状态出 发,根据位移法基本原理,从开始建立 的近似状态,逐步通过增量调整修正, 最后收敛于真实状态的渐近法。 力矩分配法计算过程简单直观,主要应用于分析连 续梁和无结点线位移的刚架。 分析中杆端转角、杆端弯矩以及固端弯矩的正负号 规定与位移法相同
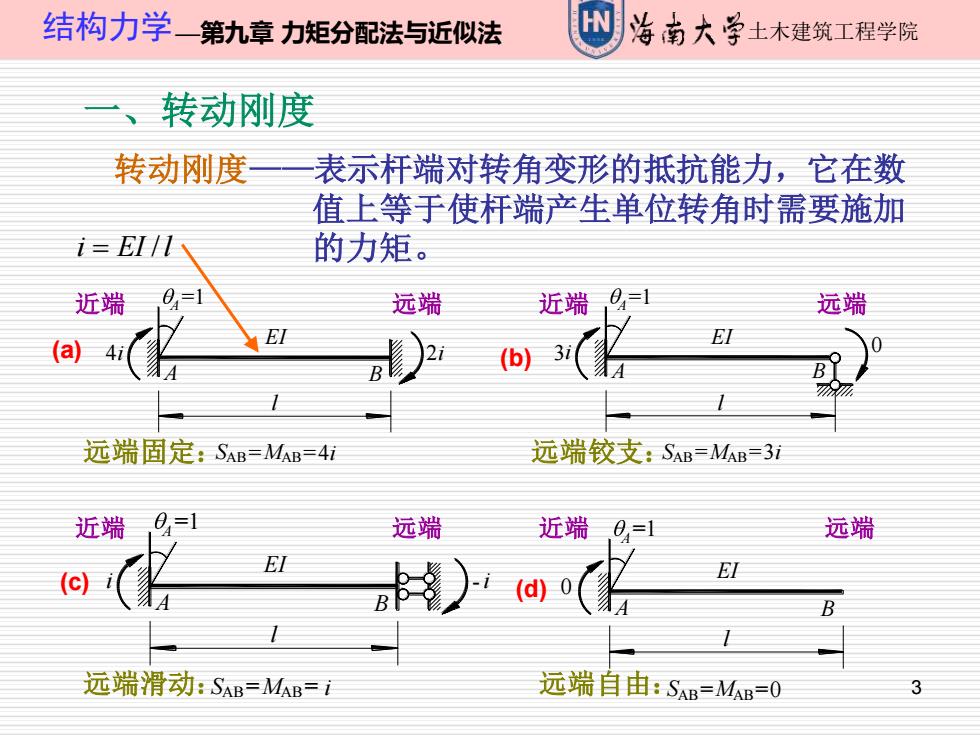
结构力学一第九章力矩分配法与近似法 洛南大学士木建筑工程学院 转动刚度 转动刚度 表示杆端对转角变形的抵抗能力,它在数 值上等于使杆端产生单位转角时需要施加 i=EII 的力矩。 近端 远端 近端 远端 (a)4i EI (b)31 远端固定:SAB=MAB=4i 远端铰支:SAB=MAB=31 近端 远端 近端0=1 远端 EI i(d0( E (c)i 远端滑动:SAB=MAB=i 远端自由:SAB=MAB=0 3
3 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 (a) 一、转动刚度 转动刚度——表示杆端对转角变形的抵抗能力,它在数 值上等于使杆端产生单位转角时需要施加 的力矩。 l EI A =1 A B 4i 2i SAB=MAB=4i (b) l A B EI A =1 3i 0 SAB=MAB=3i l EI A =1 A B i -i SAB=MAB= i l EI A =1 A B 0 SAB=MAB=0 近端 远端 近端 远端 远端 远端 近端 近端 (c) (d) 远端固定: 远端铰支: 远端滑动: 远端自由: i = EI /l
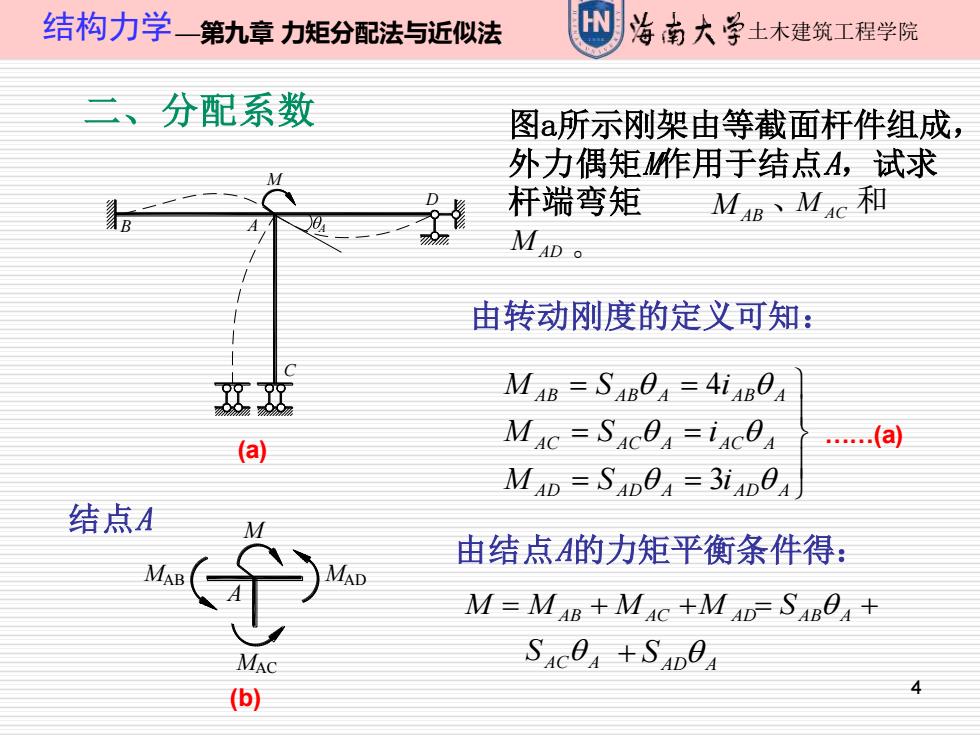
结构力学一第九章力矩分配法与近似法 海南大学土木建筑工程学院 二、分配系数 图a所示刚架由等截面杆件组成, 外力偶矩作用于结点A,试求 杆端弯矩 MB、MC和 MAD。 由转动刚度的定义可知: 这双 MAB SAB0=4iAB0 (a) MAC SAc0x=ixc0a .(a) MAD=SADθA=3iAD0 结点A 由结点A的力矩平衡条件得: AB MAD M=MAB MAC +M AD SAB0+ MAC S4C0 +S4D0 (b) 4
4 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 二、分配系数 B A D C M A MAB M AC M AD 、 和 。 图a所示刚架由等截面杆件组成, 外力偶矩M作用于结点A,试求 杆端弯矩 (a) 由转动刚度的定义可知: A M MAB MAC MAD (b) 由结点A的力矩平衡条件得: 结点A M = M AB + M AC +M AD= S AB A + S AC A + S AD A = = = = = = AD AD A AD A AC AC A AC A AB AB A AB A M S i M S i M S i 3 4 .(a)

结构力学—第九章力矩分配法与近似法 治南大学土木建筑工程学院 因而得到: M SAB +SAC+SAD 将所求得的0代入式(a)中,得: ” (b) MAD 由此可知,各杆端的弯矩与各杆端的转动刚度成正比。 5
5 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 由此可知,各杆A端的弯矩与各杆A端的转动刚度成正比。 因而得到: = + + = A AB AC AD A S M S S S M 将所求得的 A 代入式(a)中,得: = = = M S S M M S S M M S S M A AD AD A AC AC A AB AB .(b)

结构力学一第九章力矩分配法与近似法 海南大学土木建筑工程学院 令 ∑ 称为各杆在近端((即端)的分配系数。 汇交手同一刚结点的各杆杆端的分配系数之和恒等于1 即 ∑4=4粉+4C十4D=l 式b)中的计算结果可以用下列公式表示: M=HM M一一称为分配弯矩。 式(©)表示施加于结点A的外力偶矩M,可按各杆杆端的分配 系数分配给各杆的近端。 6
6 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 令 = A Aj Aj S S ——称为各杆在近端(即A端)的分配系数。 汇交于同一刚结点的各杆杆端的分配系数之和恒等于1, 即: = AB + AC + AD =1 A Aj 式 (b)中的计算结果可以用下列公式表示: M Aj ——称为分配弯矩。 式 (c)表示施加于结点A的外力偶矩M,可按各杆杆端的分配 系数分配给各杆的近端。 M Aj = AjM .(c)

结构力学一第九章力矩分配法与近似法 海南大学土木建筑工程学院 三、传递系数 传递系数一三 远端弯矩与近端弯矩的比值,用C表示。 远端固定:C= 2 远端滑动:C=1 远端铰支:C=0 将远端弯矩称为传递弯矩,按下式计算: MA=C动M霸
7 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 三、传递系数 传递系数——远端弯矩与近端弯矩的比值,用 CAj 表示。 远端固定: 2 1 C = 远端滑动: C = −1 远端铰支: C = 0 将远端弯矩称为传递弯矩,按下式计算: M jA = CAjM Aj

结构力学_一第九章力矩分配法与近似法 海南大学土木建筑工程学院 由此可知,对于只有一个刚结点的结构,该 结点只产生角位移,其杆端弯矩的求解过程可分 为两步:第一步,按各杆的分配系数求出近端弯 矩,亦即分配弯矩,此步称为分配过程;第二步, 根据各杆远端的支承情况,将近端弯矩乘以传递 系数得到远端弯矩,亦即传递弯矩,此步称为传 递过程。经过分配和传递得到各杆的杆端弯矩, 这种求解方法就是力矩分配法。 力矩分配法划分为: 单结点结构的力矩分配法 多结点结构的力矩分配法 8
8 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 由此可知,对于只有一个刚结点的结构,该 结点只产生角位移,其杆端弯矩的求解过程可分 为两步:第一步,按各杆的分配系数求出近端弯 矩,亦即分配弯矩,此步称为分配过程;第二步, 根据各杆远端的支承情况,将近端弯矩乘以传递 系数得到远端弯矩,亦即传递弯矩,此步称为传 递过程。经过分配和传递得到各杆的杆端弯矩, 这种求解方法就是力矩分配法。 力矩分配法划分为: 单结点结构的力矩分配法 多结点结构的力矩分配法
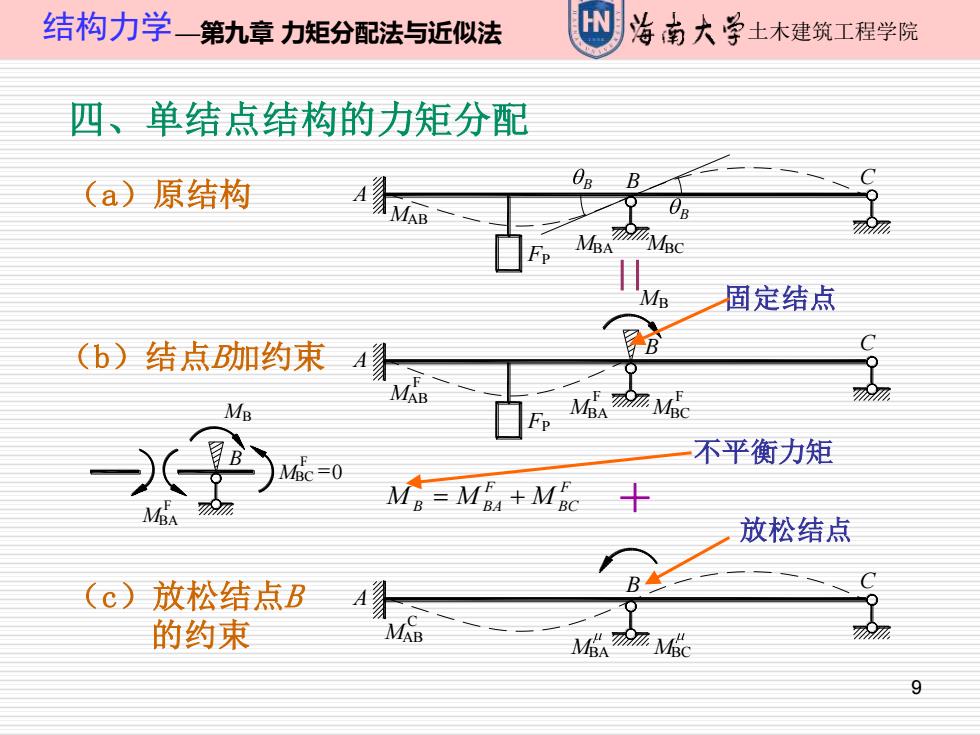
结构力学一第九章力矩分配法与近似法 W 南大学士木建筑工程学院 四、单结点结构的力矩分配 (a)原结构 B AB MBA MB 固定结点 (b)结点B咖约束A) MB =0 不平衡力矩 M=MR+MBc MBA 放松结点 (c)放松结点B A缘 的约束 MAB 9
9 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 四、单结点结构的力矩分配 A B C FP MAB MBA MBC B ( B a)原结构 A B C FP MAB F MBA F MBC F MB B MBA F MBC F MB =0 (b)结点B加约束 A B C MAB C MBA MBC (c)放松结点B 的约束 固定结点 放松结点 F BC F M B = M BA + M 不平衡力矩 +

结构力学一—第九章力矩分配法与近似法 海南大学土木建筑工程学院 单结点结构力矩分配法的计算步骤: 1.在刚结点上加上附加刚臂,把结构分为单跨梁,计算 分配系数,计算各单跨超静定梁在荷载作用下的固端 弯矩和结点的不平衡力矩: 2,去掉约束,相当于在结点上加一反向的不平衡力矩, 计算分配弯矩,将分配弯矩传至杆件的远端,求出传 递弯矩, 3.叠加各杆端的弯矩就得到实际的杆端弯矩。 10
10 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 单结点结构力矩分配法的计算步骤: 1.在刚结点上加上附加刚臂,把结构分为单跨梁,计算 分配系数,计算各单跨超静定梁在荷载作用下的固端 弯矩和结点的不平衡力矩; 3.叠加各杆端的弯矩就得到实际的杆端弯矩。 2.去掉约束,相当于在结点上加一反向的不平衡力矩, 计算分配弯矩,将分配弯矩传至杆件的远端,求出传 递弯矩;

结构力学一第九章力矩分配法与近似法 W 治南大学土木建筑工程学院 例1用力矩分配法计算图示两跨连续梁,绘出弯矩图。 15kN/m 80kN 围 2E1 4m 解:(①)计算刚结点处各杆端的分配系数 4×E SBA =4iAB= El 4 Suc=3c= 3×2E1 =1.5E1 4 SBA H —=0.4 μc= Spc =0.6 SnA+SBC 11
11 结构力学—第九章 力矩分配法与近似法 土木建筑工程学院 例1 用力矩分配法计算图示两跨连续梁,绘出弯矩图。 A B C 15kN/m 80kN EI 2EI 4m 2m 2m 解:(1)计算刚结点处各杆端的分配系数 EI EI S i BA AB = = = 4 4 4 EI EI S i BC BC 1.5 4 3 2 3 = = = = 0.4 + = BA BC BA BA S S S = 0.6 + = BA BC BC BC S S S