
结构力学一—第十一章矩阵位移法 海南大学土木建筑工程学院 第十一章矩阵位移法 11.1概述 随着计算机在各领域的不断深入应用,结构力 学这门学科也得到了进一步的发展,出现了计算机 化的结构力学(即计算结构力学)这个新的分支。 计算机辅助设计(CAD)中使用到的诸多结构 分析软件都以有限单元法(简称有限元法)为理论 依据,有限元法是一种近几十年发展起来的新方法, 从数学角度来说,它是求解偏微分方程定解问题的 数值分析方法之一;从力学角度来说,它是求取基 于变分原理的近似解的方法之一;而从我们最熟识 的工程结构的角度来说,它是结构力学的矩阵分析 方法在连续介质力学中的合理应用。由此可见
2 结构力学—第十一章 矩阵位移法 土木建筑工程学院 11.1 概述 随着计算机在各领域的不断深入应用,结构力 学这门学科也得到了进一步的发展,出现了计算机 化的结构力学(即计算结构力学)这个新的分支。 计算机辅助设计(CAD)中使用到的诸多结构 分析软件都以有限单元法(简称有限元法)为理论 依据,有限元法是一种近几十年发展起来的新方法, 从数学角度来说,它是求解偏微分方程定解问题的 数值分析方法之一;从力学角度来说,它是求取基 于变分原理的近似解的方法之一;而从我们最熟识 的工程结构的角度来说,它是结构力学的矩阵分析 方法在连续介质力学中的合理应用。由此可见 第十一章 矩阵位移法

结构力学一第十一章矩阵位移法 洛南大学士木建筑工程学院 学好结构力学的矩阵分析方法,可以为我们后续深 入学习有限元法打好基础。 结构力学的矩阵分析方法是将矩阵数学的理论 引入结构力学而得,即在进行结构矩阵分析时,仍 旧沿用传统结构力学的基本假定、基本原理和基本 方法,而在公式和各种表达式的表述方法上使用矩 阵形式。矩阵化的表述方式具有简洁、规范、易于 排错的优点,因而容易转化成计算机程序,方便计 算机软件的开发。 将力法和位移法同矩阵数学相结合,产生出矩 阵力法和矩阵位移法。相对于力法而言,位移法具 有基本结构唯一和可以求解静定结构两大优势,这 3
3 结构力学—第十一章 矩阵位移法 土木建筑工程学院 学好结构力学的矩阵分析方法,可以为我们后续深 入学习有限元法打好基础。 结构力学的矩阵分析方法是将矩阵数学的理论 引入结构力学而得,即在进行结构矩阵分析时,仍 旧沿用传统结构力学的基本假定、基本原理和基本 方法,而在公式和各种表达式的表述方法上使用矩 阵形式。矩阵化的表述方式具有简洁、规范、易于 排错的优点,因而容易转化成计算机程序,方便计 算机软件的开发。 将力法和位移法同矩阵数学相结合,产生出矩 阵力法和矩阵位移法。相对于力法而言,位移法具 有基本结构唯一和可以求解静定结构两大优势,这

结构力学一—第十一章矩阵位移法 海南大学士木建筑工程学院 些特点使得矩阵位移法更适用于进行结构分析软件 的开发。因此,本章将重点介绍平面杆件结构的矩 阵位移法。 矩阵位移法基本原理同位移法一样,仍旧以结 点位移为基本未知量,通过平衡方程求解这些基本 未知量,然后计算结构的内力。用矩阵位移法进行 结构分析的基本要点是: (1)结构离散化 将结构划分为有限个单元,各单元只在有限个 结点处相互连接。对于杆件结构,单元常取为等截 面直杆,各单元通过刚结点、铰结点等各类结点相 连组成结构,这相当于位移法中获取基本结构的这
4 结构力学—第十一章 矩阵位移法 土木建筑工程学院 些特点使得矩阵位移法更适用于进行结构分析软件 的开发。因此,本章将重点介绍平面杆件结构的矩 阵位移法。 矩阵位移法基本原理同位移法一样,仍旧以结 点位移为基本未知量,通过平衡方程求解这些基本 未知量,然后计算结构的内力。用矩阵位移法进行 结构分析的基本要点是: (1)结构离散化 将结构划分为有限个单元,各单元只在有限个 结点处相互连接。对于杆件结构,单元常取为等截 面直杆,各单元通过刚结点、铰结点等各类结点相 连组成结构,这相当于位移法中获取基本结构的这

结构力学一第十一章矩阵位移法 南大学土木建筑工程学院 步骤; (2)单元分析 单元分析的任务是获取单元杆端力与单元杆端 位移之间的关系,建立单元刚度矩阵。这相当于位 移法中获得形常数和转角位移方程的步骤。单元杆 端位移一旦求得,单元杆端力即可通过单元刚度方 程求得。 (3)整体分析 整体分析是将单元刚度矩阵按照刚度集成规则 直接形成结构刚度矩阵,并建立整体结构的刚度方 程。这相当于位移法中建立典型方程的步骤。整体 分析将打散的单元重新集成为结构,进而引入结构 的边界条件(力平衡边界条件和变形协调边界条件)
5 结构力学—第十一章 矩阵位移法 土木建筑工程学院 一步骤; (2)单元分析 单元分析的任务是获取单元杆端力与单元杆端 位移之间的关系,建立单元刚度矩阵。这相当于位 移法中获得形常数和转角位移方程的步骤。单元杆 端位移一旦求得,单元杆端力即可通过单元刚度方 程求得。 (3)整体分析 整体分析是将单元刚度矩阵按照刚度集成规则 直接形成结构刚度矩阵,并建立整体结构的刚度方 程。这相当于位移法中建立典型方程的步骤。整体 分析将打散的单元重新集成为结构,进而引入结构 的边界条件(力平衡边界条件和变形协调边界条件)

结构力学一—第十一章矩阵位移法 海南大学土木建筑工程学院 为求解结构刚度方程做好准备。 求解结构刚度方程得到各结点位移后,只需再 返回单元分析,即可求出各单元杆端力,进而绘出 结构内力图。 11.2杆件结构的离散化 11.2.1单元与结点的划分和编码 由若干根杆件组成的结构称为杆件结构。使用 矩阵位移法分析结构的第一步,是将结构“拆散” 为一根根独立的杆件,这一步骤称为离散化。为方 便起见,常将杆件结构中的等截面直杆作为矩阵位 移法的独立单元,这就必然导致结构中杆件的转折 点、汇交点、支承点、截面突变点、自由端、材料 改变 6
6 结构力学—第十一章 矩阵位移法 土木建筑工程学院 为求解结构刚度方程做好准备。 求解结构刚度方程得到各结点位移后,只需再 返回单元分析,即可求出各单元杆端力,进而绘出 结构内力图。 11.2 杆件结构的离散化 11.2.1 单元与结点的划分和编码 由若干根杆件组成的结构称为杆件结构。使用 矩阵位移法分析结构的第一步,是将结构“拆散” 为一根根独立的杆件,这一步骤称为离散化。为方 便起见,常将杆件结构中的等截面直杆作为矩阵位 移法的独立单元,这就必然导致结构中杆件的转折 点、汇交点、支承点、截面突变点、自由端、材料 改变
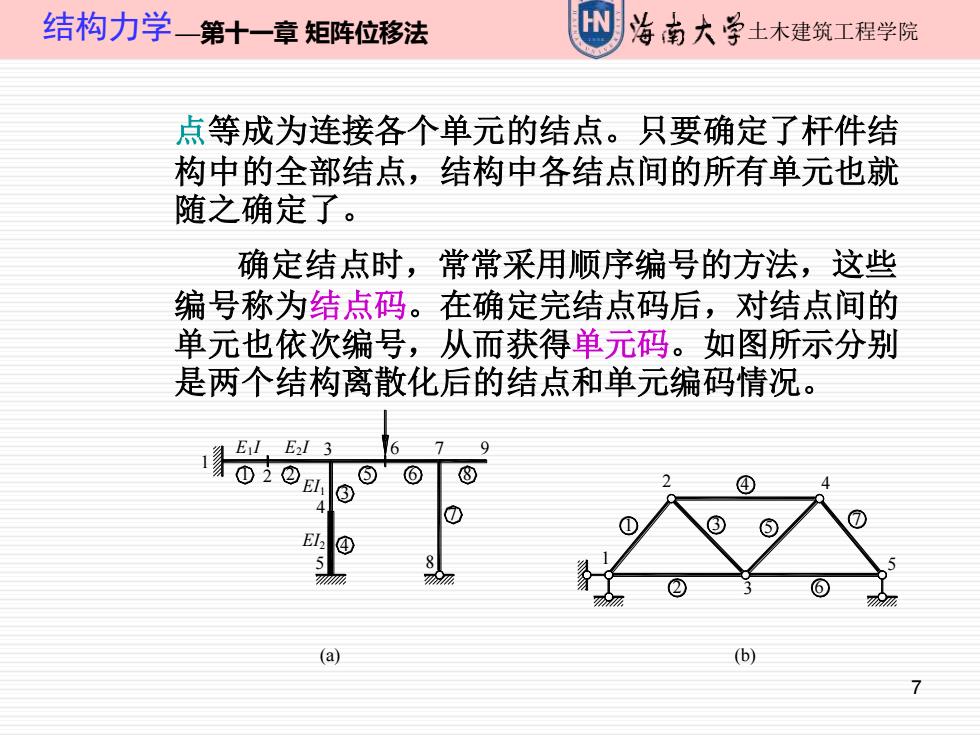
结构力学—第十一章矩阵位移法 治南大学土木建筑工程学院 点等成为连接各个单元的结点。只要确定了杆件结 构中的全部结点,结构中各结点间的所有单元也就 随之确定了。 确定结点时,常常采用顺序编号的方法,这些 编号称为结点码。在确定完结点码后,对结点间的 单元也依次编号,从而获得单元码。如图所示分别 是两个结构离散化后的结点和单元编码情况。 ELE13 6 02 ⑤⑥ ⑧ 2 ④ ① ② ⑥ (a) (b)
7 结构力学—第十一章 矩阵位移法 土木建筑工程学院 点等成为连接各个单元的结点。只要确定了杆件结 构中的全部结点,结构中各结点间的所有单元也就 随之确定了。 确定结点时,常常采用顺序编号的方法,这些 编号称为结点码。在确定完结点码后,对结点间的 单元也依次编号,从而获得单元码。如图所示分别 是两个结构离散化后的结点和单元编码情况。 EI2 EI1 E1 I 6 5 4 3 2 1 7 6 5 4 3 2 1 9 8 7 5 4 3 8 7 4 3 2 2 1 1 E2 I 5 6 (a) (b)

结构力学一第十一章矩阵位移法 W 海南大学土木建筑工程学院 11.2.2两种直角坐标系 结构离散化后,杆件单元的方向千差万别。在 作整体分析时,需要在结点处建立平衡方程,为此 又需要一个统一的计算基准坐标系。因此,这里引 入两套直角坐标系来建立后续需要研究的力和位移 等物理量之间的关系。 (1)单元坐标系 单元坐标系(又称局部坐标系)是单元分析时 使用的坐标系,它只与具体的某一单元相对应。对 结构中任意单元©,本章约定其坐标系用x-表示; 坐标系原点取为该单元一端的端结点(称为始结 点或始端);由原点指向另一端结点j(称为末结 点或末端)的方向,为杆轴x坐标正向,记作x©;
8 结构力学—第十一章 矩阵位移法 土木建筑工程学院 11.2.2 两种直角坐标系 结构离散化后,杆件单元的方向千差万别。在 作整体分析时,需要在结点处建立平衡方程,为此 又需要一个统一的计算基准坐标系。因此,这里引 入两套直角坐标系来建立后续需要研究的力和位移 等物理量之间的关系。 (1)单元坐标系 单元坐标系(又称局部坐标系)是单元分析时 使用的坐标系,它只与具体的某一单元相对应。对 结构中任意单元 e ,本章约定其坐标系用 表示; 坐标系原点取为该单元一端的端结点i(称为始结 点或始端);由原点指向另一端结点j(称为末结 点或末端)的方向,为杆轴 坐标正向,记作 ; x y − x ( ) e x

结构力学—第十一章矩阵位移法 治南大学土木建筑工程学院 以轴沿顺时针方向旋转90°为坐标轴)正向,记 作,如下图所示。 (2) v(I (2)整体坐标系 整体坐标系(又称结构坐标系)是整体分析时 使用的坐标系,它不和任何单元直接相关。设置整 9
9 结构力学—第十一章 矩阵位移法 土木建筑工程学院 以轴沿顺时针方向旋转90°为坐标轴 正向,记 作 ,如下图所示。 y ( ) e y 3 x (a) (b) 1 2 y x 1 2 3 y x (1) (1) x (2) (2) y O y 2 1 1 O 2 (2)整体坐标系 整体坐标系(又称结构坐标系)是整体分析时 使用的坐标系,它不和任何单元直接相关。设置整

结构力学一第十一章矩阵位移法 海南大学士木建筑工程学院 体坐标系的目的是使各物理量在进行整体分析时有 统一的衡量尺度。本章约定整体坐标系使用xy表 示,X轴正方向水平向右,以x轴沿顺时针方向旋转 90°为y轴正向,即y轴正方向竖直向下,整体坐标 系原点可取为任意点。 Fe③ 2) ① 立() 10
10 结构力学—第十一章 矩阵位移法 土木建筑工程学院 体坐标系的目的是使各物理量在进行整体分析时有 统一的衡量尺度。本章约定整体坐标系使用x-y表 示,x轴正方向水平向右,以x轴沿顺时针方向旋转 90°为y轴正向,即y轴正方向竖直向下,整体坐标 系原点可取为任意点。 3 x (a) (b) 1 2 y x 1 2 3 y x (1) (1) x (2) (2) y O y 2 1 1 O 2
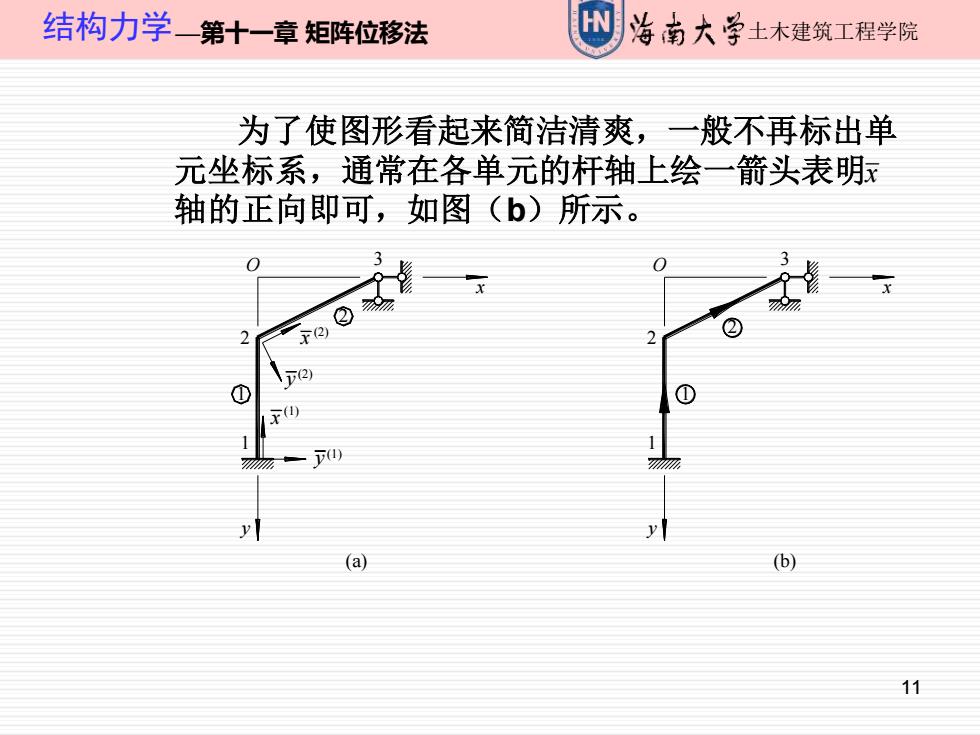
结构力学一—第十一章矩阵位移法 W 南大学士木建筑工程学院 为了使图形看起来简洁清爽,一般不再标出单 元坐标系,通常在各单元的杆轴上绘一箭头表明脉 轴的正向即可,如图(b)所示。 2) (a) (b) 11
11 结构力学—第十一章 矩阵位移法 土木建筑工程学院 为了使图形看起来简洁清爽,一般不再标出单 元坐标系,通常在各单元的杆轴上绘一箭头表明 轴的正向即可,如图(b)所示。 3 x (a) (b) 1 2 y x 1 2 3 y x (1) (1) x (2) (2) y O y 2 1 1 O 2 x