
最优控制理论与系统 第三章极小值原理及其应用 张永韡 江苏科技大学 电子信息学院 yongwzhang@gmail.com November 9,2016 4口+44在4使定)0G
最优控制理论与系统 第三章 极小值原理及其应用 张永韡 江苏科技大学 电子信息学院 yongwzhang@gmail.com November 9, 2016 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

本章主要内容 。经典变分法的局限性 。连续系统的极小值原理 。最短时间控制问题 。最少燃料控制问题 。离散系统的极小值原理 。小结 1口。1,4之1三,至分只C 三章极小位卓建及其应用 最优控制理论与系统 November 9.2016 2/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 本章主要内容 经典变分法的局限性 连续系统的极小值原理 最短时间控制问题 最少燃料控制问题 离散系统的极小值原理 小结 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 2 / 67

经典变分法的园限性 经典变分法的局限性 上面我们用经典变分法解最优控制问题时,得出了最优性的必要条件 ∂H aU =0 在得出这个条件时,作了下面的假定: ●6U是任意的,即不受限制,它遍及整个向量空间,是一个开集; 。號是存在的。 口·40,工1三型分00 三章极小值原理及其应用 最优控制理论与系统 November 9,2016 3/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典变分法的局限性 经典变分法的局限性 上面我们用经典变分法解最优控制问题时,得出了最优性的必要条件 ∂H ∂U = 0 在得出这个条件时,作了下面的假定: 1 δU 是任意的,即不受限制,它遍及整个向量空间,是一个开集; 2 ∂H ∂U 是存在的。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 3 / 67

经典变分法的局限性 在实际工程问题中,控制作用常常是有界的。如飞机舵面的偏角有限制, 火箭的推力有限制,生产过程中的生产能力有限制等等。一般,我们可 用下面的不等式来表示 lu(t≤M:i=1,…,m 这时U()=[山(t),(),…,u(t]T属于一个有界的闭集,写成 ()∈2,2为闭集。更一般的情况可用下面的不等式约束来表示。 gUt),≥0 当U(t)属于有界闭集,()在边界上取值时,6U就不是任意的了,因 为无法向边界外取值,这时盟就不一定是最优解的必要条件。 1口。t,花1三:至)只C 三章极小拉原速及其应用 最优控制理论与系统 November 9.2016 4/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典变分法的局限性 在实际工程问题中,控制作用常常是有界的。如飞机舵面的偏角有限制, 火箭的推力有限制,生产过程中的生产能力有限制等等。一般,我们可 用下面的不等式来表示 |ui(t)| ≤ Mi i = 1, · · · , m 这时 U(t) = [u1(t), u2(t), · · · , um(t)]T 属于一个有界的闭集,写成 U(t) ∈ Ω,Ω 为闭集。更一般的情况可用下面的不等式约束来表示。 g[U(t), t] ≥ 0 当 U(t) 属于有界闭集,U(t) 在边界上取值时,δU 就不是任意的了,因 为无法向边界外取值,这时 ∂H ∂U 就不一定是最优解的必要条件。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 4 / 67
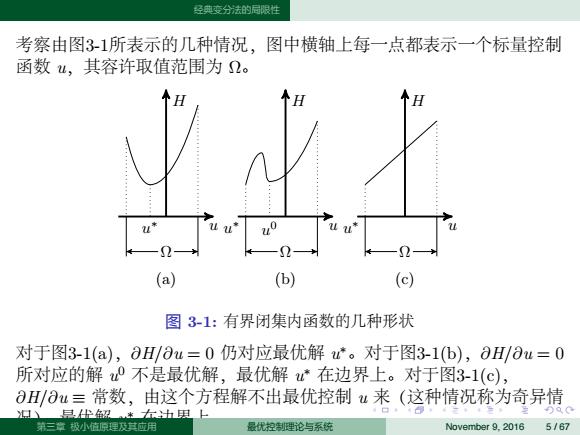
经典变分法的局限性 考察由图3-1所表示的几种情况,图中横轴上每一点都表示一个标量控制 函数山,其容许取值范围为2。 (a) (b) (c) 图3-1:有界闭集内函数的几种形状 对于图3-1(a),aH/au=0仍对应最优解产。对于图3-1(b),aH/au=0 所对应的解0不是最优解,最优解在边界上。对于图3-1(c), 0H/日u=常数,由这个方程解不出最优控制u来(这种情况称为奇异情 ▣小三尘*大h里上 第三章极小值原理及其应用 最优控制理论与系统 November 9,2016 5/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典变分法的局限性 考察由图3-1所表示的几种情况,图中横轴上每一点都表示一个标量控制 函数 u,其容许取值范围为 Ω。 u H Ω (a) u H Ω (b) u H Ω (c) u ∗ u ∗ u 0 u ∗ 图 3-1: 有界闭集内函数的几种形状 对于图3-1(a),∂H/∂u = 0 仍对应最优解 u ∗。对于图3-1(b),∂H/∂u = 0 所对应的解 u 0 不是最优解,最优解 u ∗ 在边界上。对于图3-1(c), ∂H/∂u ≡ 常数,由这个方程解不出最优控制 u 来(这种情况称为奇异情 况),最优解 u 第三章 极小值原理及其应用 ∗ 在边界上。 最优控制理论与系统 November 9, 2016 5 / 67

经典变分法的局限性 另外,0H/Ou也不一定是存在的。例如状态方程的右端X,U,)对U 的一阶偏导数可能不连续,或由于有些指标函数,如燃料最优控制问题 中,具有下面的形式 xd-a 这时HX,U,入,t)=F(X,U,t)+入TfX,U,t)对U的一阶偏导数不连续。 。经典变分法无法处理上面的情况,必须另辟新的途径。 ·极小值原理就是解决这类问题的有力工具。用极小值原理求解控制 无约束的最优控制问题和古典变分法是完全一样的。 ●1956年前苏联学者庞特里雅金提出这个原理时,把它称为极大值原 理,目前较多地采用极小值原理这个名字。 下面给出这个原理及其证明,并举例说明其应用。 日。1之1三,至只C 第三章圾小位原理及其应 最优控制理论与系统 November 9,2016 6/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典变分法的局限性 另外,∂H/∂u 也不一定是存在的。例如状态方程的右端 f(X, U, t) 对 U 的一阶偏导数可能不连续,或由于有些指标函数,如燃料最优控制问题 中,具有下面的形式 J = ∫ tf t0 F(X, U, t) dt = ∫ tf t0 |U| dt 这时 H(X, U, λ, t) = F(X, U, t) + λ Tf(X, U, t) 对 U 的一阶偏导数不连续。 经典变分法无法处理上面的情况,必须另辟新的途径。 极小值原理就是解决这类问题的有力工具。用极小值原理求解控制 无约束的最优控制问题和古典变分法是完全一样的。 1956 年前苏联学者庞特里雅金提出这个原理时,把它称为极大值原 理,目前较多地采用极小值原理这个名字。 下面给出这个原理及其证明,并举例说明其应用。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 6 / 67

连续系统的嫩小值晾理 连续系统的极小值原理 由于可以利用扩充变量的方法将各类最优控制问题化为定常系统,末值 型性能指标情况下的标准形式。我们这里只就定常系统、末值型性能指 标、固定、末端受约束情况下给出极小值原理的简单证明。 设系统的状态方程为 X=fX,U,t)X()∈Rm (3-1) 初始条件为 X(to)=Xo (3-2) 控制向量U(t)∈Rm,并受下面的约束 U∈2 (3-3) 末值状态必须满足的约束条件为 GX(),切=0 (3-4) 第三章极小值原理及其应用 最优控制理论与系统 November 9,2016 7167
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 连续系统的极小值原理 连续系统的极小值原理 由于可以利用扩充变量的方法将各类最优控制问题化为定常系统,末值 型性能指标情况下的标准形式。我们这里只就定常系统、末值型性能指 标、tf 固定、末端受约束情况下给出极小值原理的简单证明。 设系统的状态方程为 X˙ = f(X, U, t) X(t) ∈ R n (3-1) 初始条件为 X(t0) = X0 (3-2) 控制向量 U(t) ∈ Rm,并受下面的约束 U ∈ Ω (3-3) 末值状态必须满足的约束条件为 G[X(tf), tf ] = 0 (3-4) 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 7 / 67

连续系统的嫩小值原理 连续系统的极小值原理 性能指标函数为 J=X(),胡+FGX(),月 (3-5) 其中v∈R”为待定列向量。 在本节中,假设函数(XU,),號,[X,切,照存在且连续,并 假定容许控制()是在控制域内取值的任何分段连续函数。这时如果选 定了某一容许控制(),则容易证明在任意的初始条件X()=Xo下, 方程(3-1)唯一的确定了系统状态的变化规律X(),且X()是连续的和 分段可微的。在这些条件下,我们就定常系统、末值型性能指标、固 定、末端受约束情况下给出极小值原理的简单证明。 1口。t,花1三至)只C 三章极小拉原速及其应用 最优控制理论与系统 November 9.2016 8/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 连续系统的极小值原理 连续系统的极小值原理 性能指标函数为 J = ϕ[X(tf), tf ] + v TG[X(tf), tf ] (3-5) 其中 v ∈ Rn 为待定列向量。 在本节中,假设函数 fi(X, U, t),∂fi ∂X,ϕ[X(tf), tf ], ∂ϕ ∂X(tf) 存在且连续,并 假定容许控制 U(t) 是在控制域内取值的任何分段连续函数。这时如果选 定了某一容许控制 U(t),则容易证明在任意的初始条件 X(t0) = X0 下, 方程(3-1)唯一的确定了系统状态的变化规律 X(t),且 X(t) 是连续的和 分段可微的。在这些条件下,我们就定常系统、末值型性能指标、tf 固 定、末端受约束情况下给出极小值原理的简单证明。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 8 / 67
连续系统的费小值原理 极小值原理的证明 证明: 采用扰动法,即给最优控制一个变分δU,它将引起最优轨线的变分6X, 并使性能指标有一增量△J,当J为极小时,必有△J≥0,由此即可导 出最优控制所应满足的必要条件。在变分法中,δ是微量,即将最优控 制和邻近的容许控制相比较,因而最多只能建立哈密顿函数H的相对极 小值性质。 庞特里亚金极大值原理却将最优控制与控制域内所有可能的值进行比较, 因而得出结论,在整个控制域内最优控制使哈密顿函数H成为绝对极小 值。正是这个性质使得庞特里亚金极大值原理成为寻找最优控制的有力 工具。但是这样,()的改变量6U必须看成有限量,而不再是微量。 如果让改变的时间很短,则由此引起的最优轨线的改变δX仍是微量, 性能指标的增量△J也是微量,因而对各关系式的数学处理仍是比较容 易的。 0Q0 第三章极小值原理及其应用 最优控制理论与系统 November 9,2016 9167
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 连续系统的极小值原理 极小值原理的证明 证明: 采用扰动法,即给最优控制一个变分 δU,它将引起最优轨线的变分 δX, 并使性能指标有一增量 ∆J,当 J 为极小时,必有 ∆J ≥ 0,由此即可导 出最优控制所应满足的必要条件。在变分法中,δU 是微量,即将最优控 制和邻近的容许控制相比较,因而最多只能建立哈密顿函数 H 的相对极 小值性质。 庞特里亚金极大值原理却将最优控制与控制域内所有可能的值进行比较, 因而得出结论,在整个控制域内最优控制使哈密顿函数 H 成为绝对极小 值。正是这个性质使得庞特里亚金极大值原理成为寻找最优控制的有力 工具。但是这样,U(t) 的改变量 δU 必须看成有限量,而不再是微量。 如果让改变的时间很短,则由此引起的最优轨线的改变 δX 仍是微量, 性能指标的增量 ∆J 也是微量,因而对各关系式的数学处理仍是比较容 易的。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 9 / 67

连续系统的嫩小值晾理 设心()为最优控制,任选一时刻∈[o,切及一微量e>0,在时间间 隔中[-e,]给*()一有限大小的改变量6U,且使得U*+6U∈2。 现在研究由6U引起的最优轨线X*()的变化。分为三段考虑: 1,0≤t≤t-e 在这一段中,6U=0,因而X()=0。 2,-e≤t≤t 系统的状态方程(3-1)可在初始条件X(t1-e)=X”(:-e)下直接积分。 当U=U*时, r0-r-)=ix,0,d 当U=U*+6U时, X④-x白-)=厂xv+6Udt 1日。①,之·1三至分只C 三章极小原及其应 最优控制理论与系统 November 9,2016 10/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 连续系统的极小值原理 设 U∗ (t) 为最优控制,任选一时刻 t1 ∈ [t0, tf ] 及一微量 ϵ > 0,在时间间 隔中 [t1 − ϵ, t1] 给 U∗ (t) 一有限大小的改变量 δU,且使得 U∗ + δU ∈ Ω。 现在研究由 δU 引起的最优轨线 X∗ (t) 的变化。分为三段考虑: 1,0 ≤ t ≤ t1 − ϵ 在这一段中,δU = 0,因而 δX(t) = 0。 2,t1 − ϵ ≤ t ≤ t1 系统的状态方程(3-1)可在初始条件 X(t1 − ϵ) = X∗ (t1 − ϵ) 下直接积分。 当 U = U∗ 时, X ∗ (t) − X ∗ (t1 − ϵ) = ∫ t t1−ϵ f(X ∗ , U ∗ , t) dt 当 U = U∗ + δU 时, X(t) − X ∗ (t1 − ϵ) = ∫ t t1−ϵ f(X, U ∗ + δU, t) dt 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 10 / 67