
第八章控制系统的状态空间分析 一、状态空间的基本概念 1.状态反应系统运行状况,并可用一个确定系统未来行为的信息集合。 2.状态变量确定系统状态的一组独立(数目最少的)变量,如果给定了1=。时刻 这组变量的值((亿,)x亿,)…x,(亿)和1≥1,时输入的时间函数),则系 统在1≥。任何时刻(6()x()…x(0)的行为就可完全确定。 3.状态向量以状态变量为元素构成的向量,即x)=[k,(0x2()…x()。 4.状态空间以状态变量(()x2)…x()为坐标的n维空间。系统在某时 刻的状态,可用状态空间上的点来表示。 5.状态方程描述状态变量,输入变量之间关系的一阶微分方程组。 6.输出方程描述输出变量与状态变量、输入变量间函数关系的代数方程。 二、状态空间描述(状态空间表达式) 1,状态方程与输出方程合起来称为状态空间描述或状态空间表达式,线性定常系统状 态空间描述一般用矩阵形式表示,对于线性定常连续系统有 [t)=Ax(1)+Bu(t) (8-1) (t)=Cx(t)+Du(t) 对于线性定常离散系统有 [x(k+1)=Gx(k)+Hu(k) (8-2) y(k)=Cx(k)+Du(k) 2.状态空间描述的建立:系统的状态空间描述可以由系统的微分方程,结构图(方框 图),状态变量图、传递函数或脉冲传递函数(Z传递函数)等其它形式的数学模 型导出。 3.状态空间描述的线性变换及规范化(标准型) 系统状态变量的选择不是唯一的,状态变量选择不同,状态空间描述也不一样。利 用线性变换可将系统的矩阵A(见式81)规范化为四种标准型:能控标准型、能 观标准型、对角标准型、约当标准型
第八章 控制系统的状态空间分析 一、状态空间的基本概念 1. 状态 反应系统运行状况,并可用一个确定系统未来行为的信息集合。 2. 状态变量 确定系统状态的一组独立(数目最少的)变量,如果给定了 0 t = t 时刻 这组变量的值 ( ( ) ( ) ( )) 1 0 2 0 0 x t x t x t n 和 0 t t 时输入的时间函数 u(t) ,则系 统在 0 t t 任何时刻 ( ( ) ( ) ( )) 1 2 x t x t x t n 的行为就可完全确定。 3. 状态向量 以状态变量为元素构成的向量,即 ( ) ( ) ( ) ( ) 1 2 x t x t x t x t = n 。 4. 状态空间 以状态变量 ( ( ) ( ) ( )) 1 2 x t x t x t n 为坐标的 n 维空间。系统在某时 刻的状态,可用状态空间上的点来表示。 5. 状态方程 描述状态变量,输入变量之间关系的一阶微分方程组。 6. 输出方程 描述输出变量与状态变量、输入变量间函数关系的代数方程。 二、状态空间描述(状态空间表达式) 1. 状态方程与输出方程合起来称为状态空间描述或状态空间表达式,线性定常系统状 态空间描述一般用矩阵形式表示,对于线性定常连续系统有 = + = + ( ) ( ) ( ) ( ) ( ) ( ) y t Cx t Du t x t Ax t Bu t (8-1) 对于线性定常离散系统有 = + + = + ( ) ( ) ( ) ( 1) ( ) ( ) y k Cx k Du k x k Gx k Hu k (8-2) 2. 状态空间描述的建立:系统的状态空间描述可以由系统的微分方程,结构图(方框 图),状态变量图、传递函数或脉冲传递函数(Z 传递函数)等其它形式的数学模 型导出。 3. 状态空间描述的线性变换及规范化(标准型) 系统状态变量的选择不是唯一的,状态变量选择不同,状态空间描述也不一样。利 用线性变换可将系统的矩阵 A(见式 8-1)规范化为四种标准型:能控标准型、能 观标准型、对角标准型、约当标准型

三、传递函数矩阵及其实现 1.传递矩阵G(s): 多输入多输出系统的输出向量的拉氏变换与输入向量的拉氏变换之间的传递关系, 称为传递矩阵G(5),即 式中:U(s)一一系统的输入向量 Y(s)一一系统的输出向量 传递函数矩阵与多输入多输出系统状态空间描述的关系是: G(s)=C(sI-A)-B+D (8-4) 上式中的A,B,C,D即为状态空间描述{AB,C,D}中的矩阵A,B,C,D 2.传递矩阵G(s)的实现:已知系统的传递函数矩阵G(),寻找一个状态空间描述 A,B,CD},并满足式(84),则称AB,CD}为G(s)的一个实现。当系统 A,B,C,D的阶数等于传递函数矩阵G(s)的阶数时,称该系统{A,B,C,D}为 G(s)的最小实现。 传递函数矩阵的实现并不唯一。实现的常用标准形式有:可控标准形实现,可观标 准形实现、对角型实现和约当型实现等。 四、线性定常连续系统状态方程的求解 1.状态转移矩阵)(矩阵指数函数e“)及其性质。 2.计算状态转移矩阵()的方法 1)级数展开法 e=1++分m++冠4r+ (8-5) 2)拉氏变换法 0=c《sl-A0- (8-6
三、传递函数矩阵及其实现 1. 传递矩阵 G(s): 多输入多输出系统的输出向量的拉氏变换与输入向量的拉氏变换之间的传递关系, 称为传递矩阵 G(s) ,即 ( ) ( ) ( ) U s Y s G s = (8-3) 式中: U (s) ——系统的输入向量 Y(s) ——系统的输出向量 传递函数矩阵与多输入多输出系统状态空间描述的关系是: G = C I − A B+D −1 (s) (s ) (8-4) 上式中的 A,B,C,D 即为状态空间描述 A,B,C,D 中的矩阵 A,B,C,D。 2. 传递矩阵 G(s) 的实现:已知系统的传递函数矩阵 G(s) ,寻找一个状态空间描述 A,B,C,D ,并满足式(8-4),则称 A,B,C,D 为 G(s) 的一个实现。当系统 A,B,C,D 的阶数等于传递函数矩阵 G(s) 的阶数时,称该系统 A,B,C,D 为 G(s) 的最小实现。 传递函数矩阵的实现并不唯一。实现的常用标准形式有:可控标准形实现,可观标 准形实现、对角型实现和约当型实现等。 四、线性定常连续系统状态方程的求解 1. 状态转移矩阵 (t) (矩阵指数函数 At e )及其性质。 2. 计算状态转移矩阵 (t) 的方法 1) 级数展开法 At = + + ++ A n t n + k e I At A t ! 1 2! 1 2 2 (8-5) 2) 拉氏变换法 1 ( ) ( ) − t = sI − A -1 L (8-6)

3)凯莱-哈密尔顿法(又称待定系统法) 0=e-2A0 (8-7) 当矩阵A的特征值s,互异时,B()可由下式确定: R01[15s…s-Tew (8-8) … Bn-0J1ss…s-Le+ 当矩阵A具有m重特征值s,时,待定系数B,()=01,23m-l),由下式确 定(其它相异特征值按式(8-8)处理)。 1…… S8-1 ew B.(1)7 01…… -02 B() F011… n-l以n-2r (8-9) 21 21 B() 000 L(n-le 4)希尔维斯特(Sylvester)法 o-e (8-10) 54-3 式中:5(k=1,2,…m)-矩阵的特征值 一单位阵 当系统矩阵A的n个特征值互异时,用希尔维斯特方法求()最为简便。 1.性定常连续系统状态方程求解 1)齐次方程)=Ax)的解 xt)=()x(0) (8-11) 2)非齐次方程 ()=Ax(0+Bu()的解 x(1)=()x(0)+)Bu(r)dr (812) 4.线性定常连续系统的离散化 对式(8-1)表示的系统进行离散化,可导出如式(8-2)所表示的离散化状态空
3) 凯莱-哈密尔顿法(又称待定系统法) − = = = 1 0 ( ) ( ) n k k k At t e t A (8-7) 当矩阵 A 的特征值 i s 互异时, (t) k 可由下式确定: = − − − − s t s t s t n n n n n n n n e e e s s s s s s s s s t t t 2 1 2 1 1 2 2 2 2 1 1 2 1 1 1 1 0 1 1 1 ( ) ( ) ( ) (8-8) 当矩阵 A 具有 m 重特征值 1 s 时,待定系数 t (i , , , m- ) i ( ) = 01 2 3 1 ,由下式确 定(其它相异特征值按式(8-8)处理)。 − − − − = − − − − − s t n s t s t s t n n n n e n t e t e t e s n n s n s t t t 1 1 1 1 ( 1)! 2! 1! 0 0 0 1 2! ( 1)( 2) 0 1 1 1! ( 1) 0 1 1 ( ) ( ) ( ) 1 2 3 1 2 1 1 1 1 1 0 (8-9) 4) 希尔维斯特(Sylvester)法 = = − − = = n i k i k i i n k At s t s s A s I t e e k 1 1 ( ) (8-10) 式中: s k (k =1,2, n) −矩阵的特征值 I—单位阵 当系统矩阵 A 的 n 个特征值互异时,用希尔维斯特方法求 (t) 最为简便。 1. 性定常连续系统状态方程求解 1) 齐次方程 x (t) = Ax(t) 的解 x(t) = (t)x(0) (8-11) 2) 非齐次方程 x (t) = Ax(t) + Bu(t) 的解 = + − t x t t x t Bu d 0 ( ) ( ) (0) ( ) ( ) (8-12) 4.线性定常连续系统的离散化 对式(8-1)表示的系统进行离散化,可导出如式(8-2)所表示的离散化状态空

间描述。其中 G=(t) (8-13) H=[()Bdr 5.离散系统状态方程求解 1)递推法 =Gx0+2G0=2.… (8-14 2)Z变换法 X(e)=(l-G)X(0)+(e-G)HU(e) (8-15) 五、线性定常连续系统的可控性与可观测性 1.线性定常连续系统的可控性判断 rank B AB AB...AB =n (8-16) I)当系统=AX+Bu中的A矩阵为对角阵且特征根互异时,输入矩阵B中 无全零行。 2)当A为约当阵且相同特征根分布在一个约当块内时,输入矩阵B中约当块最 后一行对应的行中不全为零,且输入矩阵中与相异特征根对应的行不全为零。 3)(s-4A)B的行向量线性无关。 4)单输入系统{4,B}为可控标准型 5)单输入单输出系统,当状态空间描述导出的传递函数没有零、极点对消时, 系统可控,可观测。 2.输出可控型判据 rankCB CAB…CA-BD=g(C阵的行数) (8-17) )状态可控性与输出可控性是两个不同的概念,其间没有必然的联系。单输入 单输出系统若输出不可控,则系统或不可控或不可观测。 3.线性定常连续系统的可观测型判据 rankcr 4cr...(4)cr]=n (8-18 1)当系统的A阵为对角阵且特征根互异时,输出矩阵C无全零列。 与约当块最前 为零
间描述。其中, = = = T t T H Bd G t 0 ( ) ( ) (8-13) 5.离散系统状态方程求解 1) 递推法 x k G x G Hu i (k , , ) k i ( ) k (0) k i ( ) 1 2 1 1 1 = + = − = − − (8-14) 2) Z 变换法 ( ) ( ) (0) ( ) ( ) 1 1 X z zI G zX zI G HU z − − = − + − (8-15) 五、线性定常连续系统的可控性与可观测性 1. 线性定常连续系统的可控性判断 rankB AB A B A B n n = 2 −1 (8-16) 1) 当系统 X = AX + Bu 中的 A 矩阵为对角阵且特征根互异时,输入矩阵 B 中 无全零行。 2) 当 A 为约当阵且相同特征根分布在一个约当块内时,输入矩阵 B 中约当块最 后一行对应的行中不全为零,且输入矩阵中与相异特征根对应的行不全为零。 3) sI A B 1 ( ) − − 的行向量线性无关。 4) 单输入系统 A,B 为可控标准型。 5) 单输入/单输出系统,当状态空间描述导出的传递函数没有零、极点对消时, 系统可控,可观测。 2.输出可控型判据 rankCB CAB CAn−1B D= q (C阵的行数) (8-17) 1) 状态可控性与输出可控性是两个不同的概念,其间没有必然的联系。单输入/ 单输出系统若输出不可控,则系统或不可控或不可观测。 3.线性定常连续系统的可观测型判据 rankC A C A C n T T T T n T = −1 ( ) (8-18) 1) 当系统的 A 阵为对角阵且特征根互异时,输出矩阵 C 无全零列。 2) 当系统的 A 阵为约当阵且相同的特征值分布在一个约当块内时,输出矩阵中 与约当块最前一列对应的列不全为零,输出矩阵中与相异特征值对应的列不全 为零

3)C(sl-A)的列向量线性无关。 4)单输出系统{A,C}为可观测标准型。 六、线性定常离散系统的可控性和可观测型判据 1,可控性判据 rank H GH ..G"H=n (8-19) 2.可观测性判据 ranklcT G'cr ...(G')CT]=n (8-20) 七、线性定常系统的状态反馈与状态观测器 1.状态反馈与状态反馈控制系统的极点配置 1)状态反馈 状态反馈是将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端 与参考输入比较后形成控制率,作为受控系统的控制输入,即 ()=r()-KX() (8-21 式中: r()-参考输入 K-反馈系数向量 X()-状态向量 u()-控制输入 若受控系统的状态空间描述为 ()=AX()+Bu() (8-22) y(t)=CX(t)+Du(t) 将式(8-21)代入式(8-22)可得 X0)=(A-BK)X(t)+Bm(0) (8-23) (t)=(C-DK)X(t)+Dr(t) 上式的简化写法为{A-BK,B,C-DK,D} 2)状态反馈控制系统的极点配置 极点配置是通过计算选择状态反馈阵K,使得闭环控制系统 {A-BK,B,C-DK,D的极点(即{A-BK}的特征值)正好处于所希望的
3) 1 ( ) − C sI − A 的列向量线性无关。 4) 单输出系统 A,C 为可观测标准型。 六、线性定常离散系统的可控性和可观测型判据 1. 可控性判据 rankH GH G H n n = −1 (8-19) 2. 可观测性判据 rankC G C G C n T T T T n T = −1 ( ) (8-20) 七、线性定常系统的状态反馈与状态观测器 1. 状态反馈与状态反馈控制系统的极点配置 1) 状态反馈 状态反馈是将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端 与参考输入比较后形成控制率,作为受控系统的控制输入,即 u(t) = r(t) − KX(t) (8-21) 式中: r(t) −参考输入 控制输入 状态向量 反馈系数向量 − − − ( ) ( ) u t X t K 若受控系统的状态空间描述为 ( ) ( ) ( ) ( ) ( ) ( ) y t CX t Du t X t AX t Bu t = + = + (8-22) 将式(8-21)代入式(8-22)可得 = − + = − + ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) y t C DK X t Dr t X t A BK X t Br t (8-23) 上式的简化写法为 A− BK,B,C − DK,D 2) 状态反馈控制系统的极点配置 极点配置是通过计算选择状态反馈阵 K , 使 得 闭 环 控 制 系 统 A− BK,B,C − DK,D 的极点(即 A− BK 的特征值)正好处于所希望的
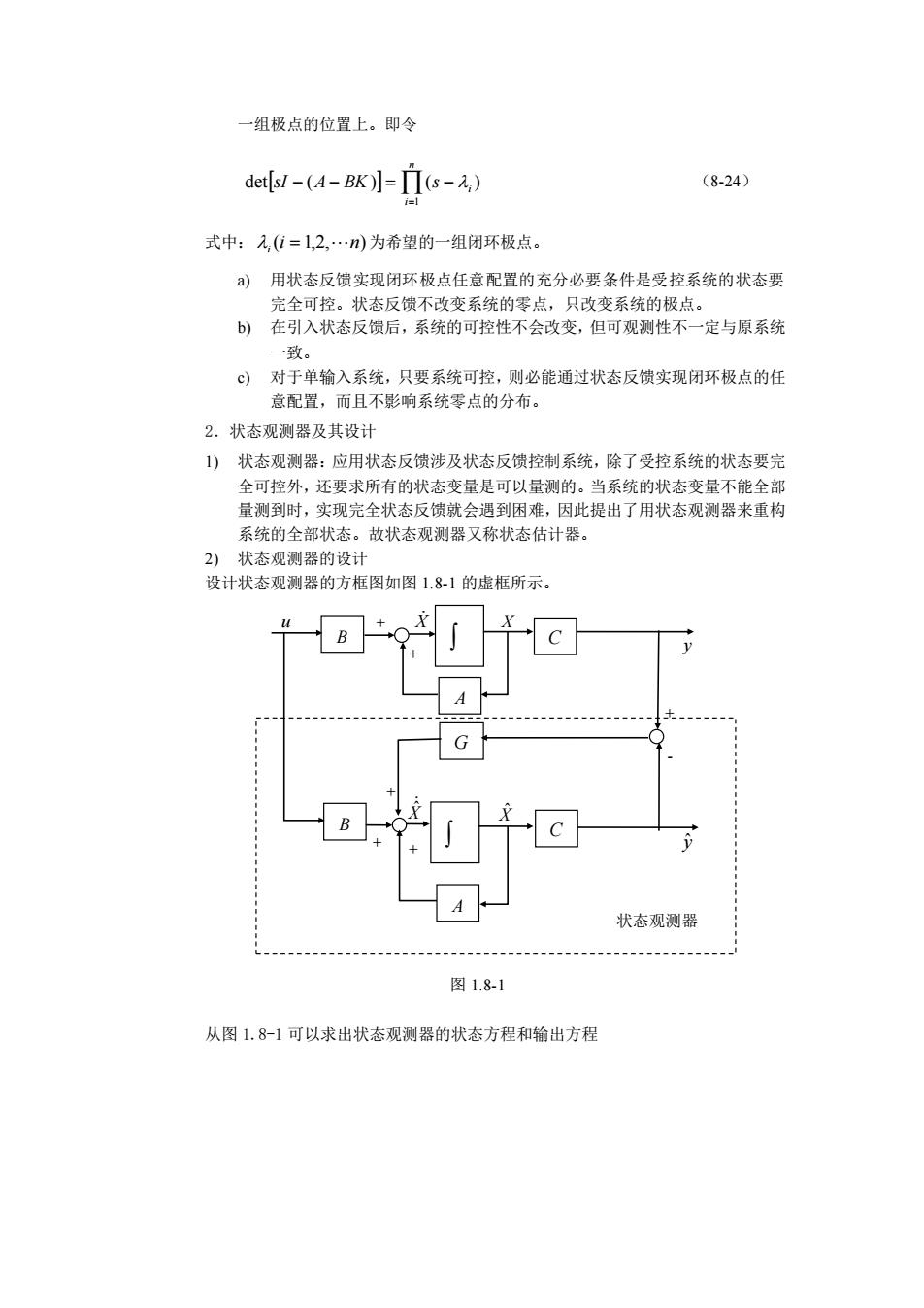
一组极点的位置上。即令 det[s/-(4-BK)]-ITs2) (8-24) 式中:,(位=1,2,…n)为希望的一组闭环极点。 )用状态反馈实现闭环极点任意配置的充分必要条件是受控系统的状态要 完全可控。状态反馈不改变系统的零点,只改变系统的极点。 b)在引入状态反馈后,系统的可控性不会改变,但可观测性不一定与原系统 一致。 ©)对于单输入系统,只要系统可控,则必能通过状态反馈实现闭环极点的任 意配置,而且不影响系统零点的分布。 2.状态观测器及其设计 )状态观测器:应用状态反馈涉及状态反馈控制系统,除了受控系统的状态要完 全可控外,还要求所有的状态变量是可以量测的。当系统的状态变量不能全音 量测到时,实现完全状态反馈就会遇到困难,因此提出了用状态观测器来重构 系统的全部状态。故状态观测器又称状态估计器。 2)状态观测器的设计 设计状态观测器的方框图如图1.81的虚框所示 B G LB一 状态观测器 图1.8-1 从图1.8-1可以求出状态观测器的状态方程和输出方程
一组极点的位置上。即令 = − − = − n i i sI A BK s 1 det ( ) ( ) (8-24) 式中: (i 1,2, n) i = 为希望的一组闭环极点。 a) 用状态反馈实现闭环极点任意配置的充分必要条件是受控系统的状态要 完全可控。状态反馈不改变系统的零点,只改变系统的极点。 b) 在引入状态反馈后,系统的可控性不会改变,但可观测性不一定与原系统 一致。 c) 对于单输入系统,只要系统可控,则必能通过状态反馈实现闭环极点的任 意配置,而且不影响系统零点的分布。 2.状态观测器及其设计 1) 状态观测器:应用状态反馈涉及状态反馈控制系统,除了受控系统的状态要完 全可控外,还要求所有的状态变量是可以量测的。当系统的状态变量不能全部 量测到时,实现完全状态反馈就会遇到困难,因此提出了用状态观测器来重构 系统的全部状态。故状态观测器又称状态估计器。 2) 状态观测器的设计 设计状态观测器的方框图如图 1.8-1 的虚框所示。 从图 1.8-1 可以求出状态观测器的状态方程和输出方程 G X X ˆ X X ˆ y y ˆ B A C u B A C + - + + + + + 状态观测器 图 1.8-1

求=A成+Gy-)+Bu =+G(y-C)+Bu (8-24 =(A-GC)+Bu+Gy =CX (8-25) 状态观测器的反馈矩阵G可由下式求出 detsl-(4-Gc)]=IT(s-) (8-26 式中:元,(i=1,2,…m)为一组希望的,可任意配置的极点,它决定了状态误差衰减 的速率。 3)状态观测器存在的基本条件 a)原系统{A,B,C}完全可观测。 b)观测器状态方程所对应的状态矩阵(A-GC)的所有特征根具有负实部。 分离定理:若原系统{A,B,C}可控可观测,当用状态观测器估计全部状态再形成全状态反 馈时,系统的极点配置和观测器设计可分别独立进行。观测器的设计不影响配置好的系统极 点,状态反馈也不影响观测器的收敛性
y CX A GC X Bu Gy AX G y CX Bu X AX G y y Bu ˆ ˆ ˆ ( ) ) ˆ ( ˆ ( ˆ) ˆ ˆ = = − + + = + − + = + − + 状态观测器的反馈矩阵 G 可由下式求出 = − − = − n i i sI A GC s 1 det ( ) ( ) (8-26) 式中: (i 1,2, n) i = 为一组希望的,可任意配置的极点,它决定了状态误差衰减 的速率。 3) 状态观测器存在的基本条件 a) 原系统 A,B,C 完全可观测。 b) 观测器状态方程所对应的状态矩阵 (A − GC) 的所有特征根具有负实部。 分离定理:若原系统 A,B,C 可控可观测,当用状态观测器估计全部状态再形成全状态反 馈时,系统的极点配置和观测器设计可分别独立进行。观测器的设计不影响配置好的系统极 点,状态反馈也不影响观测器的收敛性。 (8-24) (8-25)