第三章控制系统的时域分析 一、控制系统的时域分析法 系统加入典型输入信号后,分析其输出响应特性的动态性能和稳态性能,研究其是 否满足生产过程对控制系统的性能要求。 二、控制系统的性能指标(如图131所示) 4=±5%.±2% 1.动态性能指标: )最大超调量o,%: 1.0 b)上升时间1,: 峰值时间t。: d)调整时间1,: 0 2.稳态性能指标:稳态误差e 输出响应的稳态值与希望的给定值之间的偏差。是衡量就准确性的重要指标。 三、二阶系统的数学模型和动态性能指标计算 1.二阶系统的闭环传递函数 r d(1) G(s)=C(s) R k C(s) R(S)Ts2+s+K (3-1) s(Ts+l) 式中:T-受控对象的时间常数 图1.3-2 K一受控对象的增益 其典型结构图如附图132所示。 (31)式可改写成标准形式: G(s)=2+25a,5+0 (3-2) 式中:Q一无阻尼自然报荡频率,以一停
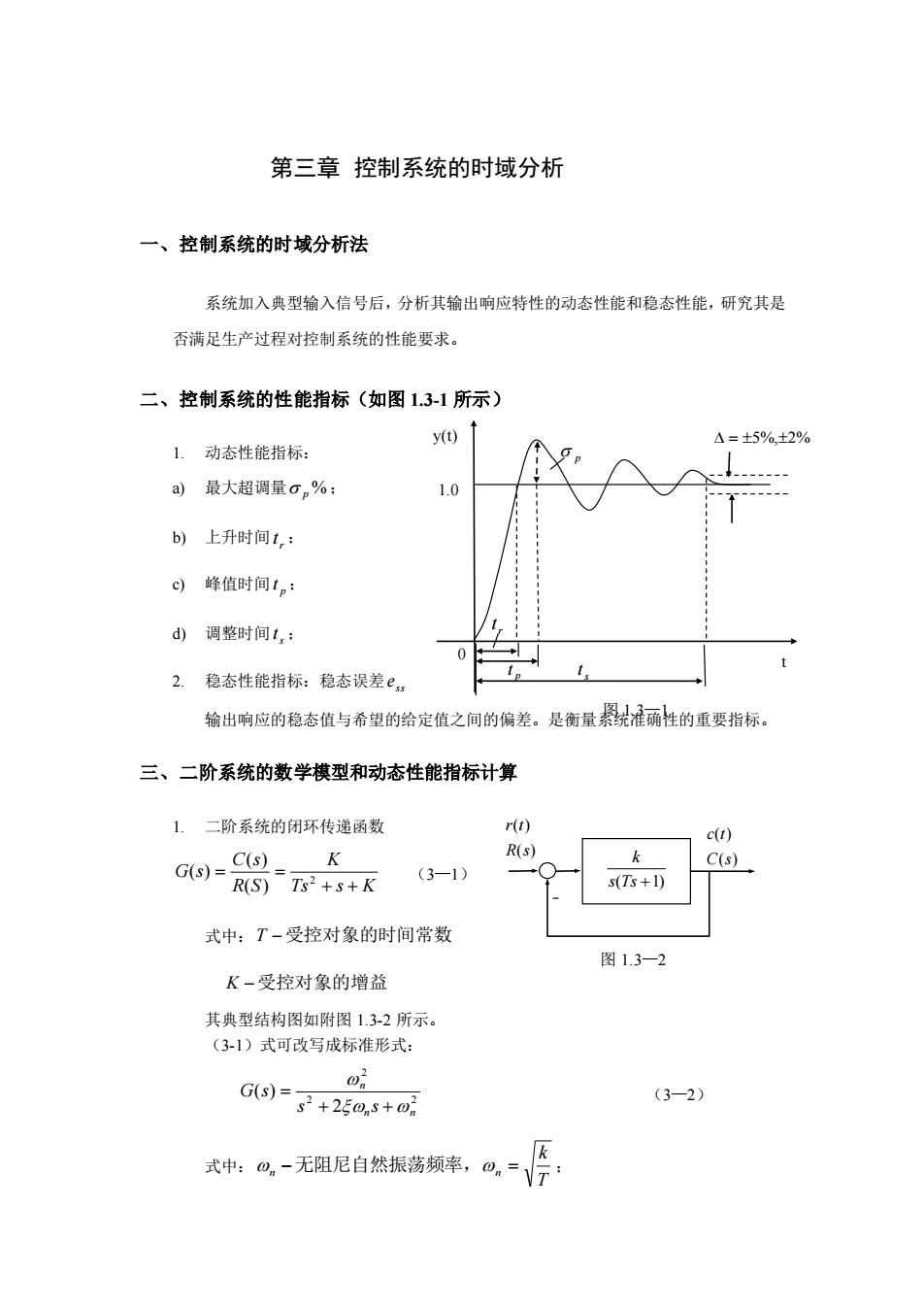
图 1.3—2 (3—1) (3—2) 第三章 控制系统的时域分析 一、控制系统的时域分析法 系统加入典型输入信号后,分析其输出响应特性的动态性能和稳态性能,研究其是 否满足生产过程对控制系统的性能要求。 二、控制系统的性能指标(如图 1.3-1 所示) 1. 动态性能指标: a) 最大超调量 p % ; b) 上升时间 r t ; c) 峰值时间 p t ; d) 调整时间 s t ; 2. 稳态性能指标:稳态误差 ss e 输出响应的稳态值与希望的给定值之间的偏差。是衡量系统准确性的重要指标。 三、二阶系统的数学模型和动态性能指标计算 1. 二阶系统的闭环传递函数 Ts s K K R S C s G s + + = = 2 ( ) ( ) ( ) 式中: T −受控对象的时间常数 K −受控对象的增益 其典型结构图如附图 1.3-2 所示。 (3-1)式可改写成标准形式: 2 2 2 2 ( ) n n n s s G s + + = 式中: T k n −无阻尼自然振荡频率,n = ; 图 1.3—1 p r t p t s t = 5%,2% 0 1.0 y(t) t ( ) ( ) R s r t s(Ts +1) k ( ) ( ) C s c t

5-阻尼比,5产27示 2.二阶系统动态性能指标的计算(0<:<1的欠阻尼情况) 司上升时间1,=-Q (3-3) 上式中:0=g-型 5 0g=0V1- 降值时间1,:,向,a.-写 (3-4) g超调量0,%=e5Fx100% (3-5) 3 (△=±5%) (36) o (A=2%) ©)其它性能指标:衰减指数m和衰减率 【.衰减指数m m=- 50 (3-7) Ⅱ.衰减率w y-e he-eim (3-8) 四、高阶系统的动态响应和简化分析 高阶系统的动态响应,在工程中常采用主导极点的概念进行简化分析。 闭环主导极点的基本概念:如果高阶系统中距离虚轴最近的一对共轭复数极点(或一个实极 点)的实部绝对值仅为其它极点的/5或更小,并且附近有没有零点,则系统的响应主要由 这一对复数极点确定,称之为闭环主导极点。找到了主导极点,高阶系统就可以近似作为 阶(或一阶)系统来分析
(3—3) (3—4) (3—5) ( = 5% ) ( = 2% ) (3—6) (3—7) (3—8) 2 TK 1 −阻尼比, = 。 2. 二阶系统动态性能指标的计算( 0 1 的欠阻尼情况) a) 上升时间 d r t − = 上式中: 2 1 1− = − tg 2 d = n 1− b) 峰值时间 2 1 : − = = n d p p t t c) 超调量 % 100% 2 / 1 = − − e p d) 调整时间 = n n s t 4 3 e) 其它性能指标:衰减指数 m和衰减率 I. 衰减指数 m d n m = − = 2 1 II. 衰减率 m e e 2 2 1 2 − = = − − 四、高阶系统的动态响应和简化分析 高阶系统的动态响应,在工程中常采用主导极点的概念进行简化分析。 闭环主导极点的基本概念:如果高阶系统中距离虚轴最近的一对共轭复数极点(或一个实极 点)的实部绝对值仅为其它极点的 1 5 或更小,并且附近有没有零点,则系统的响应主要由 这一对复数极点确定,称之为闭环主导极点。找到了主导极点,高阶系统就可以近似作为二 阶(或一阶)系统来分析

五、控制系统的稳定性分析与代数判据 1.稳定的定义:控制系统受扰动偏离了平衡状态,当扰动消除后系统能自动恢复到原 来的平衡状态,或能稳定在一个新的平衡状态,则称系统是稳定的,反之,称系统 是不稳定的。 2 控制系统稳定的充分必要条件:系统的特征根全部具有负的实部 3 防斯和赫尔维茨稳定性 )劳斯判据:系统特征多项式的各项系数均大于零,由系统特征方程各项系数列 出劳斯阵列表(劳斯阵列表的构成,详见教材),若劳斯阵列表中的第一列元 素符号均相同(即都是正数)则系统稳定。如果劳斯阵列表中第一列元素中出 现负数,则系统不稳定:第一列元素符号改变的次数,为特征方程的正实部根 的个新 2)赫尔维茨判据:由系统特征方程各项系数所构成的各阶赫尔维茨行列式的值全 部为正,则系统稳定。反之,系统不稳定。赫尔维茨行列式的构成,详见教材。 4。系统的稳定性是属于系统本身的特性,它只与自身的结构与参数有关,而 与初始条件,外界扰动的大小等无关。系统的稳定性只取决于系统的特征 根(极点),而与系统的零点无关。 六、控制系统的稳态误差及误差系数 1.误差的定义:常见的误差定义有两种 )从输出端定义的误差:系统输出量的期望值与实际值之差,即 e0=C,)-C(0 (3-9) 式中:e(t)-误差: C,()-与系统给定输入量r()相对应的期望输出量: C)-系统的实际输出量。 这种定义物理意义明确,但在实际系统中往往不可测量。故不常用。 2)从输入端定义的误差:是系统给定输入量与主反馈量之差(如图1.33所示), 即 e0=r-b) (3-.10) 式中:b)是实际输出)经反馈后送到输入端的反馈量。这样定义的误差在实 际系统中容易测量,便于进行理论分析,故在控制系统的分析中,常用这种定义的误差。 在单位反馈的控制系统中,式(3-9)和式(3-10)定义的误差是一样的。 0风e0 c) R(s) E(s)G(s) C(s) b(r) B(s) H(s) 图13一3
(3—9) 五、控制系统的稳定性分析与代数判据 1. 稳定的定义:控制系统受扰动偏离了平衡状态,当扰动消除后系统能自动恢复到原 来的平衡状态,或能稳定在一个新的平衡状态,则称系统是稳定的,反之,称系统 是不稳定的。 2. 控制系统稳定的充分必要条件:系统的特征根全部具有负的实部。 3. 劳斯和赫尔维茨稳定性代数判据 1) 劳斯判据:系统特征多项式的各项系数均大于零,由系统特征方程各项系数列 出劳斯阵列表(劳斯阵列表的构成,详见教材),若劳斯阵列表中的第一列元 素符号均相同(即都是正数)则系统稳定。如果劳斯阵列表中第一列元素中出 现负数,则系统不稳定;第一列元素符号改变的次数,为特征方程的正实部根 的个数。 2) 赫尔维茨判据:由系统特征方程各项系数所构成的各阶赫尔维茨行列式的值全 部为正,则系统稳定。反之,系统不稳定。赫尔维茨行列式的构成,详见教材。 4. 系统的稳定性是属于系统本身的特性,它只与自身的结构与参数有关,而 与初始条件,外界扰动的大小等无关。系统的稳定性只取决于系统的特征 根(极点),而与系统的零点无关。 六、控制系统的稳态误差及误差系数 1. 误差的定义:常见的误差定义有两种 1) 从输出端定义的误差:系统输出量的期望值与实际值之差,即 e(t) C (t) C(t) = r − 式中: e(t) −误差 ; 系统的实际输出量。 与系统给定输入量 相对应的期望输出量; − − ( ) ( ) ( ) C t C t r t r 这种定义物理意义明确,但在实际系统中往往不可测量。故不常用。 2) 从输入端定义的误差:是系统给定输入量与主反馈量之差(如图 1.3-3 所示), 即 e(t) = r(t) − b(t) (3-10) 式中: b(t) 是实际输出 c(t) 经反馈后送到输入端的反馈量。这样定义的误差在实 际系统中容易测量,便于进行理论分析,故在控制系统的分析中,常用这种定义的误差。 在单位反馈的控制系统中,式(3-9)和式(3-10)定义的误差是一样的。 图 1.3—3 C(s) G(s) H(s) R(s) E(s) B(s) - r(t) b(t) e(t) c(t)

2.稳态误差的定义 一个稳定的系统在给定输入或扰动输入的作用下,经历过渡过程进入稳态后的误 差,即e,=lm()。系统的稳态误差是对系统控制的准确性的度量,是系统的 稳态性能指标。 3.稳态误差的计算 1)系统的类型 般情况下,系统的开环传递函数可表示为 KII(+D) G(s)= (3-11) sΠ(T,s+) 式中:K开环放大系数: tT,-时间常数: N-开环结构中串连的积分环节数。N=0、1,2…分别称之为0型系统、 1型系统2型系统…,3型以上系统很少见。 2)计算稳态误差的方法: a)一般方法:首先判定系统的稳定性,因为只有对稳定的系统求e才有意 文。执后技装老的定文家出限发传道看版肥政 E(s) (R(S)为给定输 R(s) 入,N(s)为扰动输入)。最后利用拉氏变换的终值定理计算e,即 e..=lim e(t)=lim sE(s) (3-12) b)静态误差系数法:定义静态位置、速度、加速度误差系数K。,K,K。 K=limn Go(s):K.=lim sGo(s).K.lim sGo(s).(3-13) 上式中:G(s)-系统的开环传递函数。 则在单位阶跃输入信号的作用下,系统的稳 态误差为 1 e.=1+G,91+K, (3-14) 在单位斜坡输入信号的作用下
型系统、型系统 ,型以上系统很少见。 开环结构中串连的积分环节数。 、, 分别称之为 型系统、 , 时间常数; 1 2 3 0 1 2 0 − = − N N i Tj 2. 稳态误差的定义 一个稳定的系统在给定输入或扰动输入的作用下,经历过渡过程进入稳态后的误 差,即 e lim e(t) t ss → = 。系统的稳态误差是对系统控制的准确性的度量,是系统的 稳态性能指标。 3. 稳态误差的计算 1) 系统的类型 一般情况下,系统的开环传递函数可表示为 − = = + + = n N j j N m i i o s T s K s G s 1 1 ( 1) ( 1) ( ) (3-11) 式中: K-开环放大系数: 2) 计算稳态误差的方法: a) 一般方法:首先判定系统的稳定性,因为只有对稳定的系统求 ss e 才有意 义。然后按误差的定义求出误差传递函数 ( ) ( ) ( ) ( ) N s E s R s E s 或 ( R(s) 为给定输 入, N(s) 为扰动输入)。最后利用拉氏变换的终值定理计算 ss e ,即 lim ( ) lim ( ) 0 e e t sE s t s ss → → = = (3-12) b) 静态误差系数法:定义静态位置、速度、加速度误差系数 K p Kv Ka , , lim ( ); K lim ( ); K lim ( ); (3-13) 0 2 0 0 a 0 0 v 0 K G s sG s s G s s s s p → → → = = = 上式中: G0 (s) −系统的开环传递函数。 则在单位阶跃输入信号的作用下,系统的稳 态误差为 p s ss G s K e + = + = → 1 1 1 ( ) 1 lim 0 0 (3-14) 在单位斜坡输入信号的作用下

1 e.-lim sG (s)K. (3-15) 在单位加速度输入信号作用下 ea=回sG.K (3-16) 令静态误差系数应用的条件:只适用于控制输入()作用下的稳态误差计 算,且r()不存在前馈通道。 ©)扰动输入作用下系统稳态误差的计算 扰动输入N(s)作用下系统的误差传递函数为(见图1,3-4) E(s」 G,(s)H(s) (3-17) N(s)1+G(s)G2(s)H(s) R(s) 8Ew N(s) G() C(s) G,(s) 则扰动输入作用下的稳态误差e,为 ,H(S) -sG,sH(s) e-0=+49gw 当扰动为单位阶跃信号时 -sG2 (s)H(s)1_ -G3(0)H(0) G,(s)G,()(s)+G,(OXG,(0)H(0) 当开环增益足够大时,G(0)G2(0)HO)>1,则 e-G,(0 (3-18) 上式说明,扰动输入作用下的稳态误差主要取决于G(0),即扰动点前的传递函数G,(), 如果在G,(S)中引入积分环节,则系统在阶跃扰动作用下的稳态误差为零
C(s) ( ) 2 G s ( ) 1 G s H(s) R(s) - E(s) N(s) 图 1.3-4 v s ss sG s K e 1 ( ) 1 lim 0 0 = = → (3-15) 在单位加速度输入信号作用下 a s ss s G s K e 1 ( ) 1 lim 0 2 0 = = → (3-16) 静态误差系数应用的条件:只适用于控制输入 r(t) 作用下的稳态误差计 算,且 r(t) 不存在前馈通道。 c) 扰动输入作用下系统稳态误差的计算 扰动输入 N(s) 作用下系统的误差传递函数为(见图 1.3-4) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 2 G s G s H s G s H s N s E s + = − (3-17) 则扰动输入作用下的稳态误差 ss e 为 ( ) 1 ( ) ( ) ( ) ( ) ( ) lim ( ) lim 1 2 2 0 0 N s G s G s H s sG s H s e sE s s s ssn + − = = → → 当扰动为单位阶跃信号时 1 (0) (0) (0) 1 (0) (0) 1 ( ) ( ) ( ) ( ) ( ) lim 1 2 2 1 2 2 0 G G H G H G s G s H s s sG s H s e s ssn + − = + − = → 当开环增益足够大时, G1 (0)G2 (0)H(0) 1 ,则 (0) 1 G1 essn − (3-18) 上式说明,扰动输入作用下的稳态误差主要取决于 (0) G1 ,即扰动点前的传递函数 ( ) 1 G s , 如果在 ( ) 1 G s 中引入积分环节,则系统在阶跃扰动作用下的稳态误差为零