
6.2信号采样与保持 采样器与保持器是离散系统的两个基本环节,为了定量研究离散系统,必须用数学方法 对信号的采样过程和保持过程加以描述。 6.2.1信号采样 1.采样信号的数学表示 一个理想采样器可以看成是一个载波为理想单位脉冲序列6,()的幅值调制器,即理想 采样器的输出信号e'(),是连续输入信号)调制在载波6,()上的结果,如图6-6所示 0 60例 (o L。 图6-6信号的采样 用数学表达式描述上述调制过程,则有 e')=et)6,t (6-1) 理想单位脉冲序列δ,(t)可以表示为 6,(0=∑6t-nT (6-2) 0 其中1-nT)是出现在时刻t=nT,强度为1的单位脉冲,故式(6-)可以写为 ()=e(u-nT) 由于()的数值仅在采样瞬时才有意义,同时,假设 e)-0 t<0 所以e'(t)又可表示为 (()-dn)u-nT) (6-3 232
232 6.2 信号采样与保持 采样器与保持器是离散系统的两个基本环节,为了定量研究离散系统,必须用数学方法 对信号的采样过程和保持过程加以描述。 6.2.1 信号采样 1. 采样信号的数学表示 一个理想采样器可以看成是一个载波为理想单位脉冲序列 (t) T 的幅值调制器,即理想 采样器的输出信号 ( ) * e t ,是连续输入信号 e(t) 调制在载波 (t) T 上的结果,如图 6-6 所示。 图 6-6 信号的采样 用数学表达式描述上述调制过程,则有 ( ) ( ) ( ) * e t e t t = T (6-1) 理想单位脉冲序列 (t) T 可以表示为 = = − 0 ( ) ( ) n T t t nT (6-2) 其中 (t − nT) 是出现在时刻 t = nT ,强度为 1 的单位脉冲,故式(6-1)可以写为 = = − 0 * ( ) ( ) ( ) n e t e t t nT 由于 e(t) 的数值仅在采样瞬时才有意义,同时,假设 e(t) = 0 t 0 所以 ( ) * e t 又可表示为 * 0 ( ) ( ) ( ) n e t e nT t nT = = − (6-3)

2.采样信号的拉氏变换 对采样信号e'()进行拉氏变换,可得 Ero=4eol=4aano-nr1-2aanat-nn】 (6-4) 根据拉氏变换的位移定理,有 Lo(t-nT)]=e-mn[(t)e-"dt=e-n 所以,采样信号的拉氏变换 E'(s)=∑e(nTen (6-5) 3.连续信号与采样信号频谱的关系 由于采样信号只包括连续信号采样点上的信总,所以采样信号的频谱与连续信号的频谱 相比,要发生变化。 式(62)表明,理想单位脉冲序列6,()是周期函数,可以展开为傅氏级数的形式,即 6(-c.e (6-6) 式中,o,=2π/T,为采样角频率:cn是傅氏系数,其值为 ced 由于在-T/2,T/2☑区间中,6,()仅在1=0时有值,且elo=1,所以 c.=760h=7 (6-7) 将式(6-7)代入式(6-6),得 0=号2e (6-8) 再把式(6-8)代入式(6-1),有 c0=20e (6-9) 上式两边取拉氏变换,由拉氏变换的复数位移定理,得到
233 2. 采样信号的拉氏变换 对采样信号 ( ) * e t 进行拉氏变换,可得 ( ) [ ( )] [ ( ) ( )] ( ) [ ( )] 0 0 * * E s L e t L e nT t nT e nT L t nT n n = = − = − = = (6-4) 根据拉氏变换的位移定理,有 nTs st nTs L t nT e t e dt e − − − − = = 0 [ ( )] ( ) 所以,采样信号的拉氏变换 = − = 0 * ( ) ( ) n nTs E s e nT e (6-5) 3. 连续信号与采样信号频谱的关系 由于采样信号只包括连续信号采样点上的信息,所以采样信号的频谱与连续信号的频谱 相比,要发生变化。 式(6-2)表明,理想单位脉冲序列 (t) T 是周期函数,可以展开为傅氏级数的形式,即 + =− = n jn t T n s t c e ( ) (6-6) 式中, s = 2 /T ,为采样角频率; n c 是傅氏系数,其值为 / 2 / 2 1 ( ) s T jn t n T T c t e dt T − − = 由于在 [−T 2, T 2] 区间中, (t) T 仅在 t = 0 时有值,且 | =0 = 1 − t jn t s e ,所以 0 0 1 1 ( ) n c t dt T T + − = = (6-7) 将式(6-7)代入式(6-6),得 + =− = n jn t T s e T t 1 ( ) (6-8) 再把式(6-8)代入式(6-1),有 + =− = n jn t s e t e T e t ( ) 1 ( ) * (6-9) 上式两边取拉氏变换,由拉氏变换的复数位移定理,得到
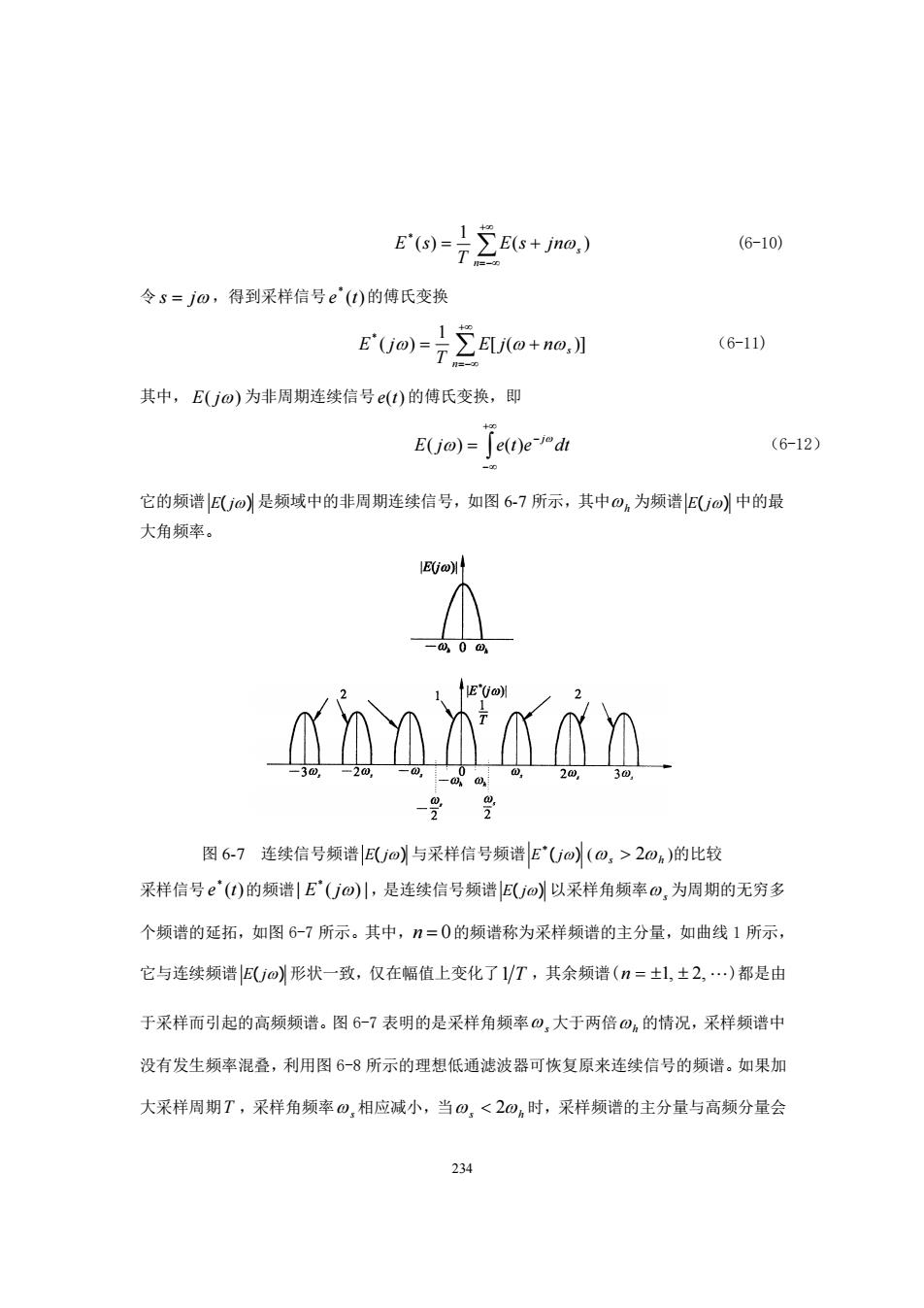
Eo)=Σs+ma,) (6-10 令s=jo,得到采样信号e'()的傅氏变换 E'Uo)=7∑Uo+n@,】 (6-11)) 其中,E(Uo)为非周期连续信号)的傅氏变换,即 Ejo)=「e)e"d (6-12) 它的频谱|E(U0)是频域中的非周期连续信号,如图67所示,其中o,为频谱EU@中的最 大角频率。 E(o) 00 ANnAn -受受 图6-7连续信号频谱Uo)与采样信号频谱E'Uo(0,>20)的比较 采样信号e'()的频谱|E(Um)儿,是连续信号频谱EU©)以采样角频率o,为周期的无穷多 个频谱的延拓,如图6-7所示。其中,=0的频谱称为采样频谱的主分量,如曲线1所示, 它与连续频谱EUo)形状一致,仅在幅值上变化了1VT,其余频谱(n=1±2,…)都是由 于采样而引起的高频频谱。图6-7表明的是采样角频率0,大于两倍0,的情况,采样频谱中 没有发生频率混叠,利用图6-8所示的理想低通滤波器可恢复原来连续信号的频谱。如果加 大采样周期T,采样角频率0,相应诚小,当0,<20,时,采样频谱的主分量与高频分量会 234
234 + =− = + n s E s jn T E s ( ) 1 ( ) * (6-10) 令 s = j ,得到采样信号 ( ) * e t 的傅氏变换 + =− = + n n s E j T E j [ ( )] 1 ( ) * (6-11) 其中, E( j) 为非周期连续信号 e(t) 的傅氏变换,即 + − − E j = e t e dt j ( ) ( ) (6-12) 它的频谱 E( j) 是频域中的非周期连续信号,如图 6-7 所示,其中 h 为频谱 E( j) 中的最 大角频率。 图 6-7 连续信号频谱 E( j) 与采样信号频谱 E ( j) ( s 2h )的比较 采样信号 ( ) * e t 的频谱 | ( ) | * E j ,是连续信号频谱 E( j) 以采样角频率 s 为周期的无穷多 个频谱的延拓,如图 6-7 所示。其中, n = 0 的频谱称为采样频谱的主分量,如曲线 1 所示, 它与连续频谱 E( j) 形状一致,仅在幅值上变化了 1 T ,其余频谱( n = 1, 2, )都是由 于采样而引起的高频频谱。图 6-7 表明的是采样角频率 s 大于两倍 h 的情况,采样频谱中 没有发生频率混叠,利用图 6-8 所示的理想低通滤波器可恢复原来连续信号的频谱。如果加 大采样周期 T ,采样角频率 s 相应减小,当 s 2h 时,采样频谱的主分量与高频分量会
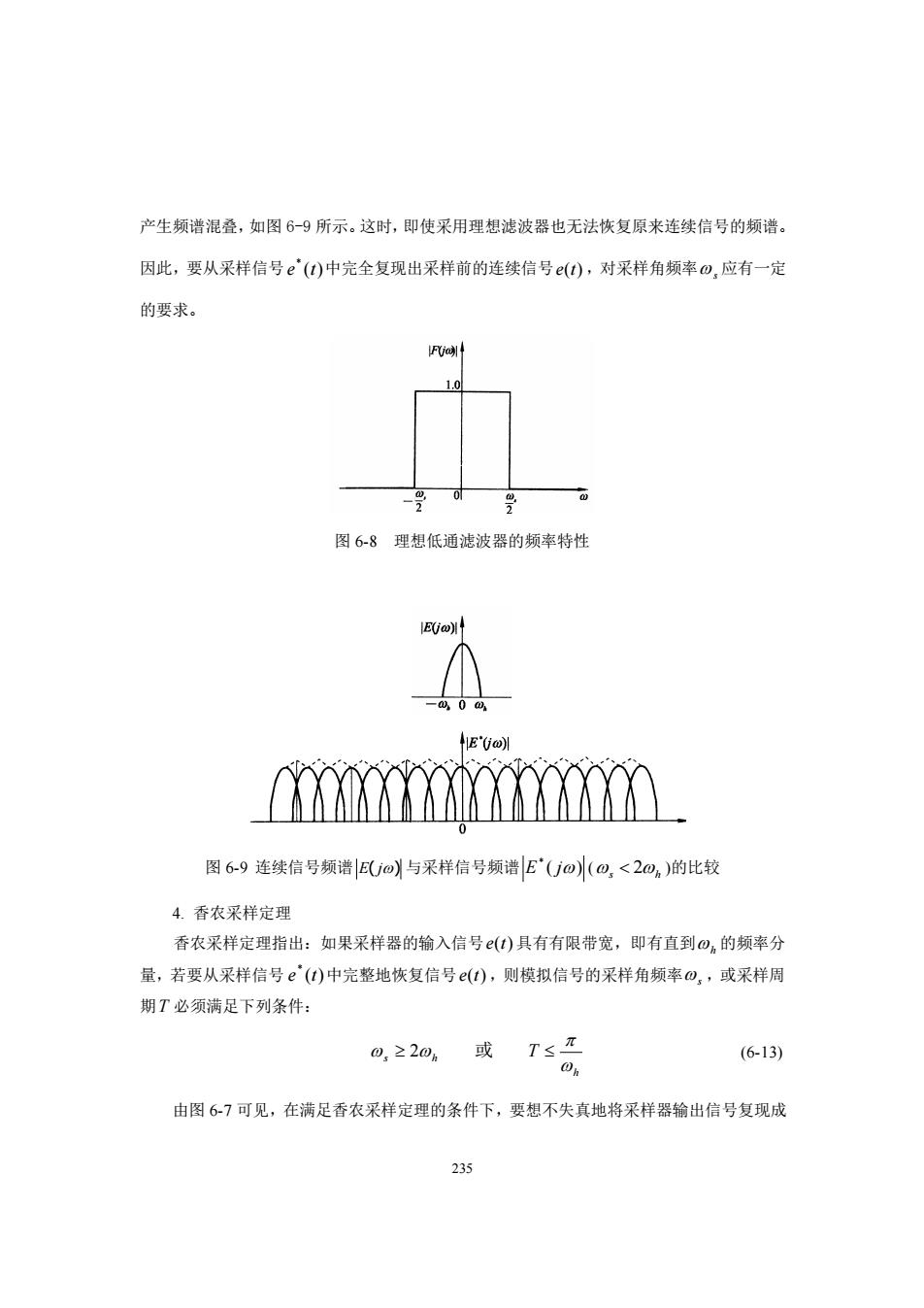
产生频谱混叠,如图6-9所示。这时,即使采用理想滤波器也无法恢复原来连续信号的频谱。 因此,要从采样信号e'()中完全复现出采样前的连续信号(),对采样角频率),应有一定 的要求。 图6-8理想低通滤波器的频率特性 HE'(joy 图6-9连续信号频谱Uo)与采样信号频谱E'(Uo水(0,<20,)的比较 4.香农采样定理 香农采样定理指出:如果采样器的输入信号(1)具有有限带宽,即有直到@的频率分 量,若要从采样信号e'()中完整地恢复信号(),则模拟信号的采样角频率0,或采样周 期T必须满足下列条件: 022成T5司 (6-13) 由图6-7可见,在满足香农采样定理的条件下,要想不失真地将采样器输出信号复现成
235 产生频谱混叠,如图 6-9 所示。这时,即使采用理想滤波器也无法恢复原来连续信号的频谱。 因此,要从采样信号 ( ) * e t 中完全复现出采样前的连续信号 e(t) ,对采样角频率 s 应有一定 的要求。 图 6-8 理想低通滤波器的频率特性 图 6-9 连续信号频谱 E( j) 与采样信号频谱 ( ) * E j ( s h 2 )的比较 4. 香农采样定理 香农采样定理指出:如果采样器的输入信号 e(t) 具有有限带宽,即有直到 h 的频率分 量,若要从采样信号 ( ) * e t 中完整地恢复信号 e(t) ,则模拟信号的采样角频率 s ,或采样周 期 T 必须满足下列条件: h s h T 2 或 (6-13) 由图 6-7 可见,在满足香农采样定理的条件下,要想不失真地将采样器输出信号复现成

原来的连续信号,需要采用图6-8所示的理想低通滤波器,然而理想低通滤波器物理上不可 实现,因此工程上常用零阶保持器。 在设计离散系统时,香农采样定理是必须亚格遵守的一条准则,它指明了从采样信号中 不失真地复现原连续信号的采样周期T的上界或采样角频率O,的下界。 6.2.2零阶保持器 为了对连续信号进行控制,需要使用保持器将控制器输出的离散信号转换为连续信号。 在工程实践中,普遍采用零阶保持器。零阶保持器把前一采样时刻nT的采样值e(nT)一直 保持到下一采样时刻(n+1)T到来之前 () 给零阶保持器输入一个理想单位脉冲),则其 单位脉冲响应函数g4()是幅值为1,持续时间为T的 矩形脉冲,如图6-10所示,它可分解为两个单位阶跃 0 T 函数的和,即 g0=10-1(1-T) (6-14) 图610零阶保持器的脉冲响应 对脉冲响应函数g()取拉氏变换,可得零阶保持器的 传递函数 G,6)=1e1-e (6-15) SS 在式(6-15)中,令3=j0,得零阶保持器的频率特性: G.o)2e(em)Tsin(Tol2) (6-16) 2jo To/2 若以采样角频率,=2π/T来表示,则上式可表示为 G,Uo=2红.n(ole,)-a (6-17) 0、π(00.) 根据上式,可画出零阶保持器的幅频特性G,(jo和相频特性∠G,(Uo)如图61所 示。由图可见,零阶保持器具有如下特性: (1)低通特性:由于幅频特性的幅值随频率值的增大而迅速衰减,说明零阶保持器基 本上是一个低通滤波器,但与理想滤波器特性相比,在。=),/2时,其幅值只有初值的 236
236 原来的连续信号,需要采用图 6-8 所示的理想低通滤波器,然而理想低通滤波器物理上不可 实现,因此工程上常用零阶保持器。 在设计离散系统时,香农采样定理是必须严格遵守的一条准则,它指明了从采样信号中 不失真地复现原连续信号的采样周期 T 的上界或采样角频率 s 的下界。 6.2.2 零阶保持器 为了对连续信号进行控制,需要使用保持器将控制器输出的离散信号转换为连续信号。 在工程实践中,普遍采用零阶保持器。零阶保持器把前一采样时刻 nT 的采样值 e(nT ) 一直 保持到下一采样时刻 (n +1)T 到来之前。 给零阶保持器输入一个理想单位脉冲 (t) ,则其 单位脉冲响应函数 g (t) h 是幅值为 1,持续时间为 T 的 矩形脉冲,如图 6-10 所示,它可分解为两个单位阶跃 函数的和,即 g (t) 1(t) 1(t T) h = − − (6-14) 对脉冲响应函数 h g (t)取拉氏变换,可得零阶保持器的 传递函数 s e s e s G s Ts Ts h − − − = − = 1 1 ( ) (6-15) 在式(6-15)中,令 s = j ,得零阶保持器的频率特性: / 2 / 2 / 2 1 2 ( ) sin( / 2) / 2 ( ) 2 / 2 j T j t j t j t jT h e e e e T G j T e j j T − − − − − − = = = (6-16) 若以采样角频率 s = 2 /T 来表示,则上式可表示为 ( ) ( ) 2 sin ( ) ( ) s j s s s h G j e − = (6-17) 根据上式,可画出零阶保持器的幅频特性 ( ) G j h 和相频特性 G ( j) h 如图 6-11 所 示。由图可见,零阶保持器具有如下特性: (1) 低通特性:由于幅频特性的幅值随频率值的增大而迅速衰减,说明零阶保持器基 本上是一个低通滤波器,但与理想滤波器特性相比,在 =s / 2 时,其幅值只有初值的 图 6-10 零阶保持器的脉冲响应

3.7%。零阶保持器除允许主要频谱分量通过外,还允许部分高频频谱分量通过,从而造 成数字控制系统的输出频谱在高频段存在纹波。 图6-11零阶保持器的频率特性 (2)相角滞后特性:由相频特性可见,零阶保持器要产生相角滞后,且随)的增大 而加大,在0=0,处,相角滞后可达-180°,从而使系统的稳定性变差。 te() e(t e(t) 4T 5T 6T 7T. T2T375 图612零阶保持器的输出特性 零阶保持器使采样信号e`(u)变成阶梯信号e()。如果把阶梯信号e()的中点连接起 来,如图6-12中点划线所示,则可以得到与连续信号()形状一致但在时间上落后T2的 响应t-T/2),相当于给系统增加了一个延迟时间为T/2的延迟环节,使系统总的相角滞 后增大,对系统的稳定性不利,这与前面零阶保持器相频分析结果是一致的
237 63.7%。零阶保持器除允许主要频谱分量通过外,还允许部分高频频谱分量通过,从而造 成数字控制系统的输出频谱在高频段存在纹波。 图 6-11 零阶保持器的频率特性 (2) 相角滞后特性:由相频特性可见,零阶保持器要产生相角滞后,且随 的增大 而加大,在 = s 处,相角滞后可达 −180 ,从而使系统的稳定性变差。 图 6-12 零阶保持器的输出特性 零阶保持器使采样信号 ( ) * e t 变成阶梯信号 e (t) h 。如果把阶梯信号 e (t) h 的中点连接起 来,如图 6-12 中点划线所示,则可以得到与连续信号 e(t) 形状一致但在时间上落后 T 2 的 响应 e(t −T 2),相当于给系统增加了一个延迟时间为 T 2 的延迟环节,使系统总的相角滞 后增大,对系统的稳定性不利,这与前面零阶保持器相频分析结果是一致的