
第3章线性系统的时域分析与校正 3.1概述 系统的数学模型建立后,便可对系统进行分析和校正。分析和校正是自动控制原理课程 的两大任务。系统分析是由已知的系统模型确定系统的性能指标:校正是根据需要在系统中 加入一些机构和装置并确定相应的参数,用以改善系统性能,使其满足所要求的性能指标。 系统分析的目的在于“认识”系统,系统校正的目的在于“改造”系统。系统的分析校正方 法一般有时域法、根轨迹法和频域法,本章介绍时域法。 3.1.1时域法的作用和特点 时域法是一种直接在时间域中对系统进行分析校正的方法,具有直观,准确的优点,它 可以提供系统时间响应的全部信息,但在研究系统参数改变引起系统性能指标变化的趋势这 一类问愿,以及对系统进行校正设计时,时域法不是非常方便。时域法是最基本的分析方法, 该方法引出的概念、方法和结论是以后学习复域法、频域法等其他方法的基础。 3.1.2时域法常用的典型输入信号 要确定系统性能的优劣,就要在同样的输入条件激励下比较系统的行为。为了在符合实 际情况的基础上便于实现和分析计算,时域分析法中一般采用如表31中的典型输入信号。 3.1.3系统的时域性能指标 如第一章所述,对控制系统的一般要求归纳为稳、准、快。工程上为了定量评价系统性 能好坏,必须给出控制系统的性能指标的准确定义和定量计算方法。 稳定是控制系统正常运行的基本条件。系统稳定,其响应过程才能收敛,研究系统的性 能(包括动态性能和稳态性能)才有意义。 实际物理系统都存在惯性,输出量的改变是与系统所储有的能量有关的。系统所储有的 能量的改变需要有一个过程。在外作用微励下系统从一种稳定状态转换到另一种稳定状态需 要一定的时间。一个稳定系统的典型阶跃响应如图31所示。响应过程分为动态过程(也称 为过渡过程)和稳态过程,系统的动态性能指标和稳态性能指标就是分别针对这两个阶段定
57 第 3 章 线性系统的时域分析与校正 3.1 概 述 系统的数学模型建立后,便可对系统进行分析和校正。分析和校正是自动控制原理课程 的两大任务。系统分析是由已知的系统模型确定系统的性能指标;校正是根据需要在系统中 加入一些机构和装置并确定相应的参数,用以改善系统性能,使其满足所要求的性能指标。 系统分析的目的在于“认识”系统,系统校正的目的在于“改造”系统。系统的分析校正方 法一般有时域法、根轨迹法和频域法,本章介绍时域法。 3.1.1 时域法的作用和特点 时域法是一种直接在时间域中对系统进行分析校正的方法,具有直观,准确的优点,它 可以提供系统时间响应的全部信息,但在研究系统参数改变引起系统性能指标变化的趋势这 一类问题,以及对系统进行校正设计时,时域法不是非常方便。时域法是最基本的分析方法, 该方法引出的概念、方法和结论是以后学习复域法、频域法等其他方法的基础。 3.1.2 时域法常用的典型输入信号 要确定系统性能的优劣,就要在同样的输入条件激励下比较系统的行为。为了在符合实 际情况的基础上便于实现和分析计算,时域分析法中一般采用如表 3-1 中的典型输入信号。 3.1.3 系统的时域性能指标 如第一章所述,对控制系统的一般要求归纳为稳、准、快。工程上为了定量评价系统性 能好坏,必须给出控制系统的性能指标的准确定义和定量计算方法。 稳定是控制系统正常运行的基本条件。系统稳定,其响应过程才能收敛,研究系统的性 能(包括动态性能和稳态性能)才有意义。 实际物理系统都存在惯性,输出量的改变是与系统所储有的能量有关的。系统所储有的 能量的改变需要有一个过程。在外作用激励下系统从一种稳定状态转换到另一种稳定状态需 要一定的时间。一个稳定系统的典型阶跃响应如图 3-1 所示。响应过程分为动态过程(也称 为过渡过程)和稳态过程,系统的动态性能指标和稳态性能指标就是分别针对这两个阶段定
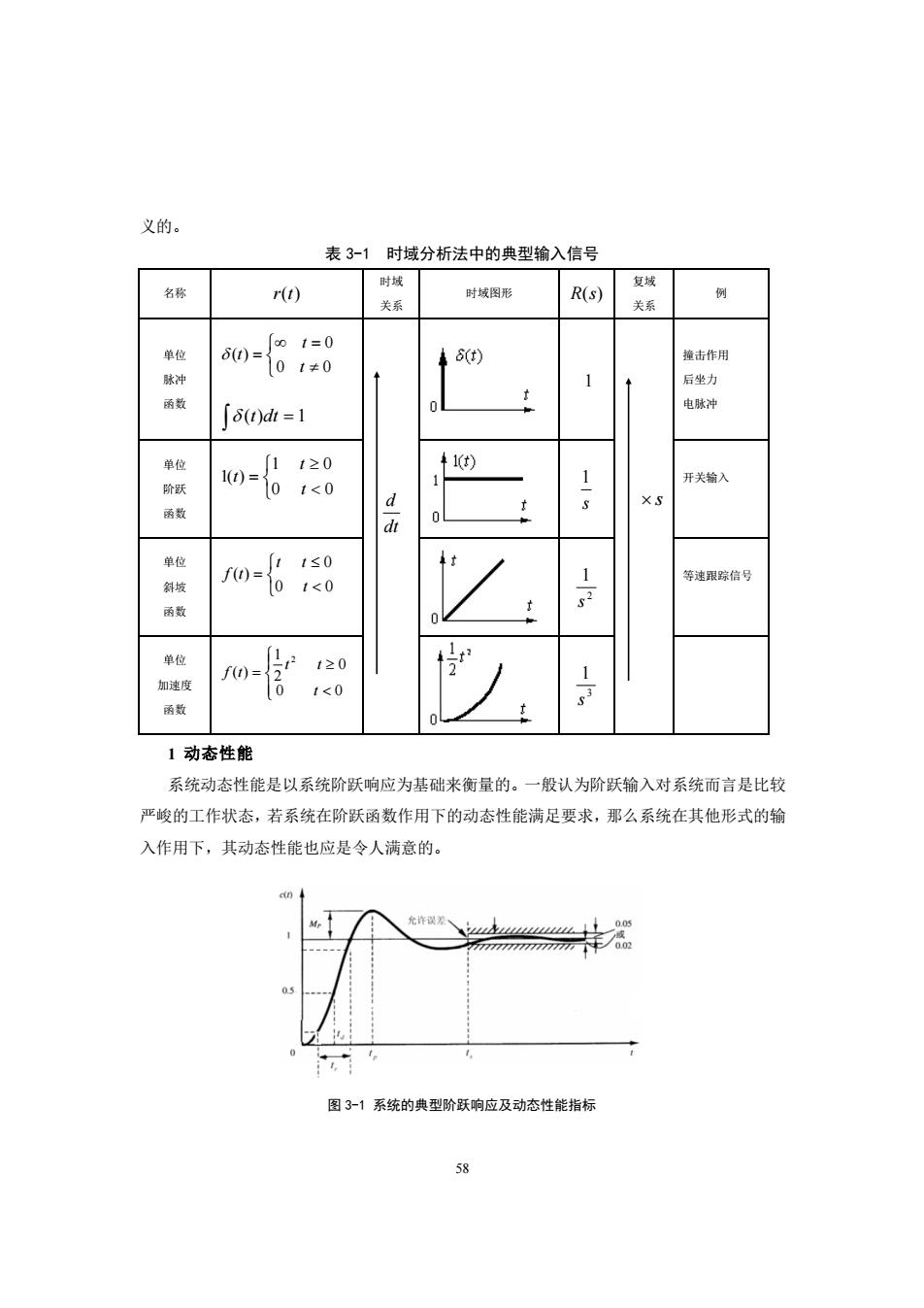
义的。 表3-1时域分析法中的典型输入信号 时域 复域 名称 r(t) 关系 时城图形 R(s) 关系 例 单位 ) 撞击作用 冲 a0-60 1 后坐力 雨数 「8)d=1 电耿冲 单位 除跃 0=68 开关输入 函数 01 单位 m-68 等速跟踪信号 斜坡 单位 知速度 1<0 函数 1动态性能 系统动态性能是以系统阶跃响应为基础来衡量的。一般认为阶跃输入对系统而言是比较 严峻的工作状态,若系统在阶跃函数作用下的动态性能满足要求,那么系统在其他形式的输 入作用下,其动态性能也应是令人满意的。 图3-1系统的典型阶跃响应及动态性能指标
58 义的。 表 3-1 时域分析法中的典型输入信号 名称 r(t) 时域 关系 时域图形 R(s) 复域 关系 例 单位 脉冲 函数 = = 0 0 0 ( ) t t t (t)dt = 1 dt d 1 s 撞击作用 后坐力 电脉冲 单位 阶跃 函数 = 0 0 1 0 1( ) t t t s 1 开关输入 单位 斜坡 函数 = 0 0 0 ( ) t t t f t 2 1 s 等速跟踪信号 单位 加速度 函数 = 0 0 0 2 1 ( ) 2 t t t f t 3 1 s 1 动态性能 系统动态性能是以系统阶跃响应为基础来衡量的。一般认为阶跃输入对系统而言是比较 严峻的工作状态,若系统在阶跃函数作用下的动态性能满足要求,那么系统在其他形式的输 入作用下,其动态性能也应是令人满意的。 图 3-1 系统的典型阶跃响应及动态性能指标

动态性能指标通常有如下几项: 延迟时间1,阶跃响应第一次达到终值h(∞)的50%所需的时间。 上升时间1,阶跃响应从终值的10%上升到终值的90%所需的时间:对有振荡的系统, 也可定义为从0到第一次达到终值所需的时间。 峰值时间1。阶跃响应越过终值(o)达到第一个峰值所需的时间。 调节时间1。阶跃响应到达并保持在终值h(∞)士5%误差带内所需的最短时间:有时也 用终值的±2%误差带来定义调节时间。除非特别说明,本书以后所说的调节时间均以±5% 误差带定义。 超调量o%峰值h(t。)超出终值h(o)的百分比,即 0%=- h(t)-h(c) ×100% (3-1) h(oo) 在上述动态性能指标中,工程上最常用的是调节时间1。(描述“快”),超调量σ%(描 述“匀”)以及峰值时间1。,它们也是本书重点讨论的动态性能指标。 2稳态性能 稳态误差是时间趋于无穷时系统实际输出与理想输出之间的误差,是系统控制精度或抗 干扰能力的一种度量。稳态误差有不同定义(具体请参阅第3.6节),通常在典型输入下进 行测定或计算。 应当指出,系统性能指标的确定应根据实际情况而有所侧重。例如,民航客机要求飞行 平稳,不允许有超调:歼击机则要求机动灵活,响应迅速,允许有适当的超调:对于一些启 动之后便需要长期运行的生产过程(如化工过程等)则往往更强调稳态精度。 %
59 动态性能指标通常有如下几项: 延迟时间 d t 阶跃响应第一次达到终值 h() 的 50%所需的时间。 上升时间 r t 阶跃响应从终值的 10%上升到终值的 90%所需的时间;对有振荡的系统, 也可定义为从 0 到第一次达到终值所需的时间。 峰值时间 p t 阶跃响应越过终值 h() 达到第一个峰值所需的时间。 调节时间 s t 阶跃响应到达并保持在终值 h() 5 %误差带内所需的最短时间;有时也 用终值的 2 %误差带来定义调节时间。除非特别说明,本书以后所说的调节时间均以 5 % 误差带定义。 超调量 % 峰值 ( ) p h t 超出终值 h() 的百分比,即 % 100 ( ) ( ) ( ) − = h h t p h % (3-1) 在上述动态性能指标中,工程上最常用的是调节时间 s t (描述“快”),超调量 %(描 述“匀”)以及峰值时间 p t ,它们也是本书重点讨论的动态性能指标。 2 稳态性能 稳态误差是时间趋于无穷时系统实际输出与理想输出之间的误差,是系统控制精度或抗 干扰能力的一种度量。稳态误差有不同定义(具体请参阅第 3.6 节),通常在典型输入下进 行测定或计算。 应当指出,系统性能指标的确定应根据实际情况而有所侧重。例如,民航客机要求飞行 平稳,不允许有超调;歼击机则要求机动灵活,响应迅速,允许有适当的超调;对于一些启 动之后便需要长期运行的生产过程(如化工过程等)则往往更强调稳态精度