
2.3控制系统的复域数学模型 控制系统的微分方程是在时间域描述系统动态性能的数学模型,在给定外作用及初始条 件下,求解微分方程可以得到系统输出响应的全部时间信息。这种方法直观、准确,但是如 果系统的结构改变或某个参数变化时,就要重新列写并求解微分方程,不便于对系统分析和 设计。 传递函数是在拉氏变换基础上的复数域中的数学模型。传递函数不仅可以表征系统的动 态特性,而且可以用来研究系统的结构或参数变化对系统性能的影响。经典控制理论中广泛 应用的根轨迹法和频域法,就是以传递函数为基础建立起来的,因此传递函数是经典控制理 论中最基本也是最重要的数学模型。 2.3.1传递函数 1.传递函数的定义 传递函数是在零初始条件下,线性定常系统输出量的拉氏变换与输入量的拉氏变换之 比。 线性定常系统的微分方程一般为 a.ddd)a de()()= al" d司 al 0t+0+0 (2-25) d 式中:c(0为输出:)为输入量:a,an1,a及bn,b1b均为由系统结构、参 数决定的常系数。 在零初始条件下对式(2-25)两端进行拉氏变换,可得相应的代数方程 (a,s+an3+.+a3+a)C(s)=(bns"+bms1++bs+b)R(s)(2-26) 系统的传递函数为 C⊙_b+bS1++65+6=G6 R(s)a,5"+a1s-l+.…+a,5+a0 (2-27)
22 2.3 控制系统的复域数学模型 控制系统的微分方程是在时间域描述系统动态性能的数学模型,在给定外作用及初始条 件下,求解微分方程可以得到系统输出响应的全部时间信息。这种方法直观、准确,但是如 果系统的结构改变或某个参数变化时,就要重新列写并求解微分方程,不便于对系统分析和 设计。 传递函数是在拉氏变换基础上的复数域中的数学模型。传递函数不仅可以表征系统的动 态特性,而且可以用来研究系统的结构或参数变化对系统性能的影响。经典控制理论中广泛 应用的根轨迹法和频域法,就是以传递函数为基础建立起来的,因此传递函数是经典控制理 论中最基本也是最重要的数学模型。 2.3.1 传递函数 1.传递函数的定义 传递函数是在零初始条件下,线性定常系统输出量的拉氏变换与输入量的拉氏变换之 比。 线性定常系统的微分方程一般为 1 1 1 0 1 1 1 1 0 1 ( ) ( ) ( ) ... ( ) ( ) ( ) ( ) ... ( ) n n n n n n m m m m m m d c t d c t dc t a a a a c t dt dt dt d r t d r t dr t b b b b r t dt dt dt − − − − − − + + + + = + + + + (2-25) 式中: ct() 为输出; rt() 为输入量; 1 0 an , an− ,...,a 及 1 0 bm , bm− ,...,b 均为由系统结构、参 数决定的常系数。 在零初始条件下对式(2-25)两端进行拉氏变换,可得相应的代数方程 1 1 1 1 0 1 1 0 ( .... ) ( ) ( ... ) ( ) n n m m n n m m a s a s a s a C s b s b s b s b R s − − + + + + = + + + + − − (2-26) 系统的传递函数为 ( ) ... ... ( ) ( ) 1 0 1 1 1 0 1 1 G s a s a s a s a b s b s b s b R s C s n n n n m m m m = + + + + + + + + = − − − − (2-27)

传递函数是在零初始条件下定义的。零初始条件有两方面含义:一是指输入作用是在 1=0以后才作用于系统,因此,系统输入量及其各阶导数在1≤0时均为零:二是指输入 作用于系统之前,系统是“相对静止”的,即系统输出量及各阶导数在1≤0时的值也为 零。大多数实际工程系统都满足这样的条件。零初始条件的规定不仅能简化运算,而且有利 于在同等条件下比较系统性能。所以,这样规定是必要的。 例2-6试求例2-1中的R-LC无源网络的传递函数。 解由例21式(2-3)可知RLC无源网络的微分方程为 在零初始条件下,对上式两端取拉氏变换并整理可得网络传递函数 Ou 实际求元部件传递函数时必须考虑负载效应,所求的传递函数应当反映元部件正常带载 时工作的特性。比如,电动机空载时的特性不能反映带载运行时的特性 2.传递函数的性质 ()传递函数是复变量5的有理分式,它具有复变函数的所有性质。因为实际物理系统 总是存在惯性,并且能源功率有限,所以实际系统传递函数的分母阶次总是大于或等于分 子阶次m,即n≥m。 (②)传递函数只取决于系统的结构参数,与外作用无关。 (3)传递函数与微分方程有直接联系。 ()传递函数的拉氏反变换即为系统的脉冲响应,因此传递函数能反映系统运动特性。 因为单位脉冲函数的拉氏变换式为1(即:R(s)=L[)=1),因此有 rkaolr}-kalao (2-28) 应当注意传递函数的局限性及适用范围。传递函数是从拉氏变换导出的,拉氏变换是 种线性变换,因此传递函数只适应于描述线性定常系统。传递函数是在零初始条件下定义的, 所以它不能反映非零初始条件下系统的自由响应运动规律。 2.3.2常用控制元件的传递函数 1.电位器
23 传递函数是在零初始条件下定义的。零初始条件有两方面含义:一是指输入作用是在 t = 0 以后才作用于系统,因此,系统输入量及其各阶导数在 t 0 时均为零;二是指输入 作用于系统之前,系统是“相对静止”的,即系统输出量及各阶导数在 t 0 时的值也为 零。大多数实际工程系统都满足这样的条件。零初始条件的规定不仅能简化运算,而且有利 于在同等条件下比较系统性能。所以,这样规定是必要的。 例 2-6 试求例 2-1 中的 R-L-C 无源网络的传递函数。 解 由例 2-1 式(2-3)可知 R-L-C 无源网络的微分方程为 ( ) ( ) ( ) ( ) 2 2 u t u t dt du t RC dt d u t LC c r c c + + = 在零初始条件下,对上式两端取拉氏变换并整理可得网络传递函数 1 1 ( ) ( ) ( ) 2 + + = = U s LCs RCs U s G s r c 实际求元部件传递函数时必须考虑负载效应,所求的传递函数应当反映元部件正常带载 时工作的特性。比如,电动机空载时的特性不能反映带载运行时的特性。 2.传递函数的性质 ⑴ 传递函数是复变量 s 的有理分式,它具有复变函数的所有性质。因为实际物理系统 总是存在惯性,并且能源功率有限,所以实际系统传递函数的分母阶次 n 总是大于或等于分 子阶次 m,即 n≥m。 ⑵ 传递函数只取决于系统的结构参数,与外作用无关。 ⑶ 传递函数与微分方程有直接联系。 ⑷ 传递函数的拉氏反变换即为系统的脉冲响应,因此传递函数能反映系统运动特性。 因为单位脉冲函数的拉氏变换式为 1(即: R s L t ( ) ( ) 1 = = ),因此有 ( ) ( ) ( ) ( ) ( ) 1 1 1 L C s k t R s C s L G s L = = = − − − (2-28) 应当注意传递函数的局限性及适用范围。传递函数是从拉氏变换导出的,拉氏变换是一 种线性变换,因此传递函数只适应于描述线性定常系统。传递函数是在零初始条件下定义的, 所以它不能反映非零初始条件下系统的自由响应运动规律。 2.3.2 常用控制元件的传递函数 1.电位器
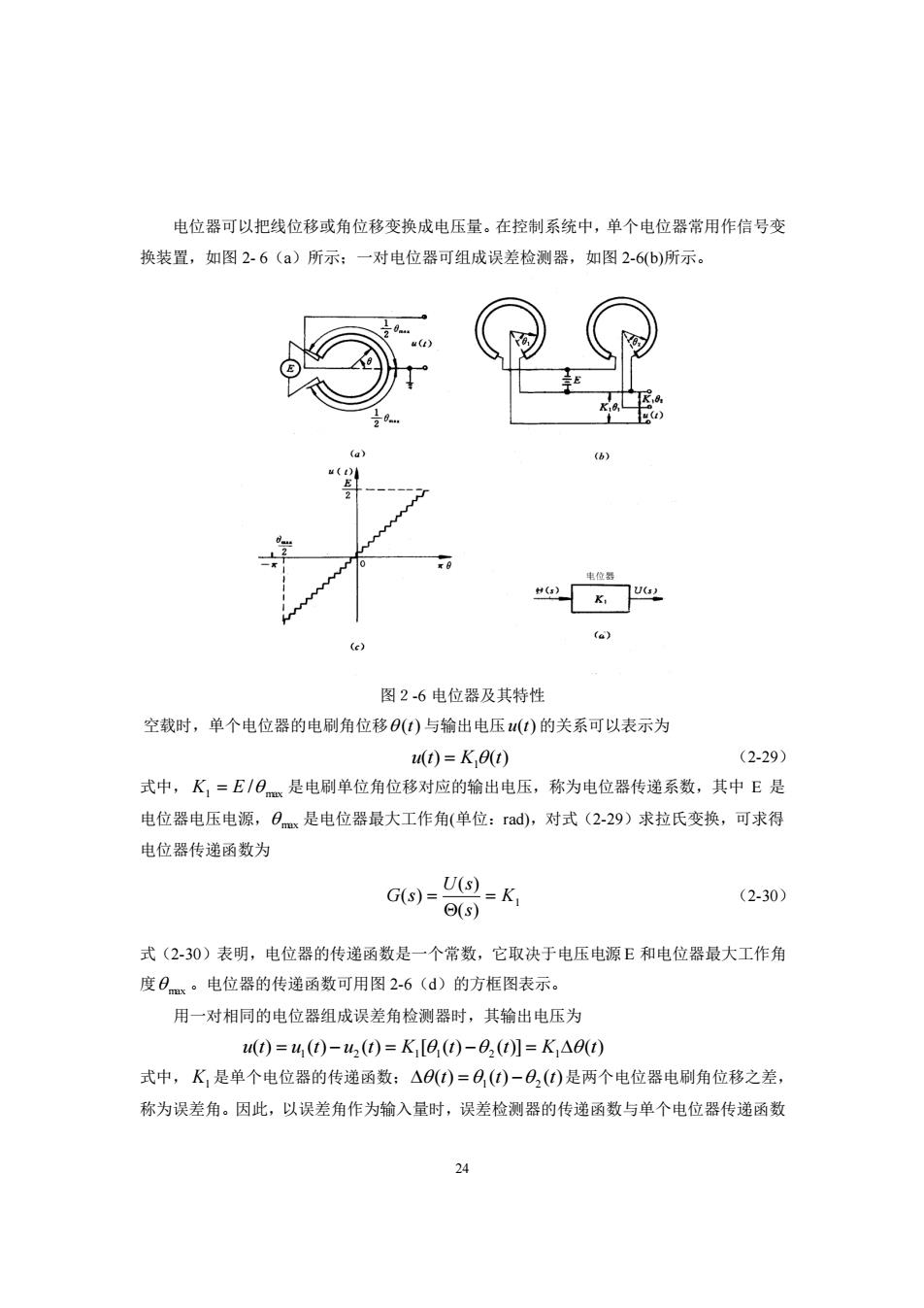
电位器可以把线位移或角位移变换成电压量。在控制系统中,单个电位器常用作信号变 换装置,如图2-6(a)所示:一对电位器可组成误差检测器,如图2-6(b)所示。 () 位器 四K☐ fu) 图2-6电位器及其特性 空载时,单个电位器的电刷角位移()与输出电压()的关系可以表示为 u(1)=K 0(1) (2-29) 式中,K,=E/日是电刷单位角位移对应的输出电压,称为电位器传递系数,其中E是 电位器电压电源,日m是电位器最大工作角(单位:rad,对式(2-29)求拉氏变换,可求得 电位器传递函数为 Gs)=y 5 (2-30) 式(230)表明,电位器的传递函数是一个常数,它取决于电压电源E和电位器最大工作角 度0x。电位器的传递函数可用图2-6(d)的方框图表示。 用一对相同的电位器组成误差角检测器时,其输出电压为 4)=40-4(0=K[0,(0-0()=K,△0) 式中,K是单个电位器的传递函数:△(t)=O(t)-O,()是两个电位器电刷角位移之差, 称为误差角。因此,以误差角作为输入量时,误差检测器的传递函数与单个电位器传递函数 2
24 电位器可以把线位移或角位移变换成电压量。在控制系统中,单个电位器常用作信号变 换装置,如图 2- 6(a)所示;一对电位器可组成误差检测器,如图 2-6(b)所示。 图2-6 电位器及其特性 空载时,单个电位器的电刷角位移 (t) 与输出电压 u(t) 的关系可以表示为 ( ) ( ) 1 u t = K t (2-29) 式中, 1 max K = E / 是电刷单位角位移对应的输出电压,称为电位器传递系数,其中 E 是 电位器电压电源, max 是电位器最大工作角(单位:rad),对式(2-29)求拉氏变换,可求得 电位器传递函数为 1 ( ) ( ) ( ) K s U s G s = = (2-30) 式(2-30)表明,电位器的传递函数是一个常数,它取决于电压电源 E 和电位器最大工作角 度 max 。电位器的传递函数可用图 2-6(d)的方框图表示。 用一对相同的电位器组成误差角检测器时,其输出电压为 ( ) ( ) ( ) [ ( ) ( )] ( ) 1 2 1 1 2 1 u t = u t −u t = K t − t = K t 式中, K1 是单个电位器的传递函数; ( ) ( ) ( ) 1 2 t = t − t 是两个电位器电刷角位移之差, 称为误差角。因此,以误差角作为输入量时,误差检测器的传递函数与单个电位器传递函数

形式相同,即为 G==K (2-31) Ae(s) 在使用电位器时应注意其负载效应。负载效应是指在元部件输出端接有负载时所产生 的影响。图2-7表示电位器输出端接有负载电 阻R,时的电路图,设电位器电阻为R。,回 路电流为 E-u0_0+ u(s) Rp-Rp Rp R 整理可得电位器输出电压为 图28电位器的负载效应 u)= E0(t) = +R01-0] (2-32) R。R 可见,由于负载电阻R,的影响,输出电压)与电刷角位移()不再保持线性关系 如果负载电阻R,很大,例如,R210R,时,可以近似得到 (0≈E0)/0m=K,)。 2.自整角机 自整角机由一个发送器和一个接收器(也称控制变压器)组成,其原理图及连接方法如 图2-8所示。它的工作原理如下。 在发送器的转子单相绕组上加上交流激磁电压e,()=Esnm后,在发送器上就产生 脉动磁通·,使定子三相绕组中产生电流,该电流在接收器中产生一脉动磁通女。当 0。=90°+0,时,转子绕组则不感应通中.,输出(0=0,当0.≠90°+0,时,克在接收 机转子绕组中产生感应电势(),其大小为 e(t)=K,cos(0,-0)sin ot (2-33) E K,-0,-00 (2-34) 式中K,一自整角机灵敏度(V/C): E一误差电压:
25 形式相同,即为 1 ( ) ( ) ( ) K s U s G s = = (2-31) 在使用电位器时应注意其负载效应。负载效应是指在元部件输出端接有负载时所产生 的影响。图 2-7 表示电位器输出端接有负载电 阻 RL 时的电路图,设电位器电阻为 Rp ,回 路电流为 ' ' ( ) ( ) ( ) P P P L E u t u t u t R R R R − = + − 整理可得电位器输出电压为 ' max ' max max ( ) ( ) ( ) ( ) (1 ) [1 (1 )] p p p p p L p L E E t u t R R R R t t R R R R = = + − + − (2-32) 可见,由于负载电阻 RL 的影响,输出电压 u(t) 与电刷角位移 (t) 不再保持线性关系, 如果负载电阻 RL 很大,例如, 10 R R L p 时,可以近似得到 ( ) ( )/ ( ) max 1 u t E t = K t 。 2.自整角机 自整角机由一个发送器和一个接收器(也称控制变压器)组成,其原理图及连接方法如 图 2-8 所示。它的工作原理如下。 在发送器的转子单相绕组上加上交流激磁电压 e (t) E sint 1 = 1 后,在发送器上就产生 脉动磁通 r ,使定子三相绕组中产生电流,该电流在接收器中产生一脉动磁通 c 。当 c = + r 90 时,转子绕组则不感应通 c ,输出 e(t) = 0 ,当 c + r 90 时, c 在接收 机转子绕组中产生感应电势 e(t) ,其大小为 e t K t ( ) = s cos( r − c )sin (2-33) r c e s E E K = − = (2-34) 式中 Ks —自整角机灵敏度( V C ); E —误差电压;
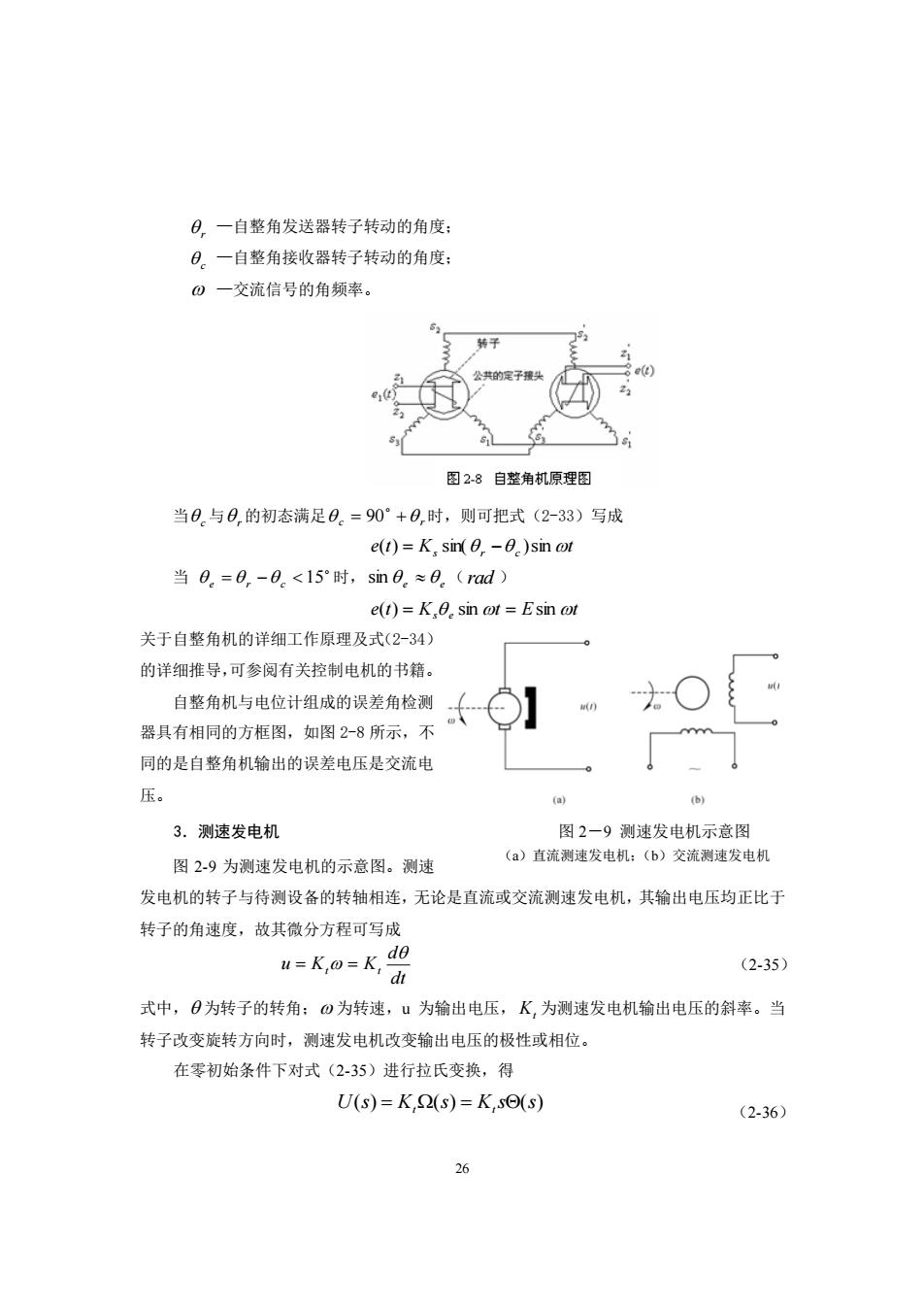
日,一自整角发送器转子转动的角度: 日。一自整角接收器转子转动的角度 0一交流信号的角频率。 子 图28自整角机原理图 当0。与0的初态满足0。=90°+0,时,则可把式(2-33)写成 e(t)=K.sin 0-0)sin oot 当0.=0,-0。<15°时,sin8.≈6。(rad) e(t)=K.0.sm ot Esin ot 关于自整角机的详细工作原理及式(234) 的详细推导,可参阅有关控制电机的书籍。 自整角机与电位计组成的误差角检测 器具有相同的方框图,如图2-8所示,不 同的是自整角机输出的误差电压是交流电 压。 a 3.测速发电机 图2一9测速发电机示意图 图2-9为测速发电机的示意图。测速 (a)直流测速发电机:(b)交流测速发电机 发电机的转子与待测设备的转轴相连,无论是直流或交流测速发电机,其输出电压均正比于 转子的角速度,故其微分方程可写成 I=Ko=水9 (2-35) 式中,O为转子的转角:0为转速,u为输出电压,K,为测速发电机输出电压的斜率。当 转子改变旋转方向时,测速发电机改变输出电压的极性或相位。 在零初始条件下对式(2-35)进行拉氏变换,得 U(s)=K,(s)=K,se(s) (2-36)
26 r —自整角发送器转子转动的角度; c —自整角接收器转子转动的角度; —交流信号的角频率。 当 c 与 r 的初态满足 c = + r 90 时,则可把式(2-33)写成 e t K t ( ) = s sin( r − c )sin 当 e = r − c 15 时, e e sin ( rad ) e t K t E t ( ) = s e sin = sin 关于自整角机的详细工作原理及式(2-34) 的详细推导,可参阅有关控制电机的书籍。 自整角机与电位计组成的误差角检测 器具有相同的方框图,如图 2-8 所示,不 同的是自整角机输出的误差电压是交流电 压。 3.测速发电机 图 2-9 为测速发电机的示意图。测速 发电机的转子与待测设备的转轴相连,无论是直流或交流测速发电机,其输出电压均正比于 转子的角速度,故其微分方程可写成 dt d u Kt Kt = = (2-35) 式中, 为转子的转角; 为转速,u 为输出电压, Kt 为测速发电机输出电压的斜率。当 转子改变旋转方向时,测速发电机改变输出电压的极性或相位。 在零初始条件下对式(2-35)进行拉氏变换,得 U(s) K (s) K s (s) = t = t (2-36) 图 2-9 测速发电机示意图 (a)直流测速发电机;(b)交流测速发电机

于是,可得测速发电机的传递函数为 Gs==K或G=8=K 2(s) ⊙s) (2-37) 式(2-37)中的两式都可表示测速发电机的传递函数,只是当输入量取转速()时用 前者,输入量取转角()时用后者。 可见,对同一个元部件,若输入输出物理量选择不同,对应的传递函数就不同。 4.电枢控制直流电动机 由例2-3可知,直流电动机的微分方程为 T.da0+o0=K,4.0-KM.0 忽略负载力矩的影响,在零初始条件下对上式进行拉氏变换,考虑4()对系统的作用, 可得电枢控制直流电动机的传递函数为 2(s) G,8)=0T.s+ K (2-38) 若电动机的输出用角位移()表示,则传递函数还可表示成如下形式: K。 U.(s)s(T.s+1) (2-39) 5.两相异步电机 两相异步电动机具有重量轻、惯性小、加速特性好的优点,是控制系统中广泛应用的 种小功率交流执行机构。 两相异步电动机由相互垂直配置的两相定子线圈和一个高电阻值的转子组成。定子线圈 的一相是激磁绕组,另一相是控制绕组,通常接在功率放大器的输出端,提供数值和极性可 变的交流控制电压。 两相异步电动机的转矩-速度特性曲线有负的斜率,且呈非线性。图2-10()是不同控制 电压山。时,试验测取的一组机械特性曲线。考虑到在控制系统中,异步电动机一般工作在 零转速附近,作为线性化的一种方法,通常把低速部分的线性段延伸到高速范围,用低速直 线近似代替非线性特性,如图210(b)中虚线所示。此外,也可用小偏差线性化方程。一般, 27
27 于是,可得测速发电机的传递函数为 Kt s U s G s = = ( ) ( ) ( ) 或 K s s U s G s = t = ( ) ( ) ( ) (2-37) 式(2-37)中的两式都可表示测速发电机的传递函数,只是当输入量取转速 (t) 时用 前者,输入量取转角 (t) 时用后者。 可见,对同一个元部件,若输入输出物理量选择不同,对应的传递函数就不同。 4.电枢控制直流电动机 由例 2-3 可知,直流电动机的微分方程为 ( ) ( ) ( ) ( ) t K u t K M t dt d t Tm + = a a − c c 忽略负载力矩的影响,在零初始条件下对上式进行拉氏变换,考虑 u (t) a 对系统的作用, 可得电枢控制直流电动机的传递函数为 ( ) 1 ( ) ( ) + = = T s K U s s G s m a a a (2-38) 若电动机的输出用角位移 (t) 表示,则传递函数还可表示成如下形式: ( ) ( 1) ( ) ( ) + = = s T s K U s s G s m a a a (2-39) 5.两相异步电机 两相异步电动机具有重量轻、惯性小、加速特性好的优点,是控制系统中广泛应用的一 种小功率交流执行机构。 两相异步电动机由相互垂直配置的两相定子线圈和一个高电阻值的转子组成。定子线圈 的一相是激磁绕组,另一相是控制绕组,通常接在功率放大器的输出端,提供数值和极性可 变的交流控制电压。 两相异步电动机的转矩-速度特性曲线有负的斜率,且呈非线性。图 2-10(b)是不同控制 电压 a u 时,试验测取的一组机械特性曲线。考虑到在控制系统中,异步电动机一般工作在 零转速附近,作为线性化的一种方法,通常把低速部分的线性段延伸到高速范围,用低速直 线近似代替非线性特性,如图 2-10(b)中虚线所示。此外,也可用小偏差线性化方程。一般

两相异步电动机机械特性的线性化方程可表示为 M=-Co@m+M, (2-40) 式中,Mn是电动机输出转矩:om是电动机的角速度:C。=dM/dom是阻尼系数, 即机械特性线性化的直线斜率:M,是堵转转矩,由图2-10(b)可求得M,=Cy4。,其中Cy 可用额定电压山。=E时的堵转转矩确定,即CM=M,/E。 75 8100 507 25分 ( 速度 (a) 图2-10两相异步电机及其特性曲线 电动机输出转矩M.用来驱动负载并克服黏性摩擦,由牛顿定律可得转矩平衡方程为 (2-41) d d 式中,日是电动机转子角位移;J和厂分别是折算到电动机轴上的总转动惯量和总黏 性摩擦系数。 由式(2-40和式(241)消去中间变量M,和M.,并在零初始条件下求拉氏变换。令 U.(s)=u,1O(s)=L0(),可求得两相异步电动机的传递函数为 a0-88u元G可 (2-42) 式中,Km=Cy/f。+C。)是电动机传递系数:Tm=Jmfm+Ca)是电动机时间常数。 由于2(s)=sO(s),故式(242)也可写为 G-2 U.(s)T.s+1 (2-43)
28 两相异步电动机机械特性的线性化方程可表示为 M C M m m s = − + (2-40) 式中, M m 是电动机输出转矩; m 是电动机的角速度; C dM d = m m 是阻尼系数, 即机械特性线性化的直线斜率; Ms 是堵转转矩,由图 2-10(b) 可求得 Ms = CM ua ,其中 CM 可用额定电压 ua = E 时的堵转转矩确定,即 CM = Ms E 。 电动机输出转矩 M m 用来驱动负载并克服黏性摩擦,由牛顿定律可得转矩平衡方程为 dt d f dt d M J m m m m m = + 2 2 (2-41) 式中, m 是电动机转子角位移; m J 和 m f 分别是折算到电动机轴上的总转动惯量和总黏 性摩擦系数。 由式(2-40)和式(2-41)消去中间变量 Ms 和 M m ,并在零初始条件下求拉氏变换。令 U (s) L[u (t)], (s) L[ (t)] a = a m = m ,可求得两相异步电动机的传递函数为 ( ) ( ) ( 1) ( ) ( ) + = + + = = s T s K s J s f C C U s s G s m m m m M a m (2-42) 式中, ( ) = +C K C f m M m 是电动机传递系数; ( ) = +C T J f m m m 是电动机时间常数。 由于 (s) s (s) m = ,故式(2-42)也可写为 ( ) 1 ( ) ( ) + = = T s K U s s G s m m a m (2-43)

式(2-42)和式(243)是两相异步电动机传递函数的两种不同形式,它们与直流电动机的传递函 数在形式上完全相同。 6.齿轮系 在许多控制系统中常用高转速、小转矩电动机来 电动枫,于 组成执行机构,而负载通常要求低转速、大转矩进行 调整,需要引入减速器进行匹配。减速器一般是一个 齿轮组,它们在机械系统中的作用相当于电气系统中 的变压器。如图2-11所示,主动齿轮与从动齿轮的转 z,目 速和齿数分别用0、乙,和0,乙2表示。一级齿轮 图2-11齿轮组 的传动比定义为 4会 (2-44) 控制系统一般用减速齿轮系,故1>1。明显地,一级齿轮减速器的传递函数可写为 22(s)_1 G(s)()h (2-45) 为了考虑负载和齿轮系对电动机特性的影响,一般要将负载和齿轮系的力矩、转动惯量 以及黏滞摩擦折合到电动机轴上进行计算。依据牛顿定律列写电机轴上的力矩平衡方程,可 以导出折算到电动机轴上的转动惯量和黏滞摩擦系数分别为 =+ f=f+京万 对于多级齿轮系,折算到电机轴上的等效转动惯量和等效黏滞摩擦系数分别为 J=+白+ -)}2J3+… (2-46 。 =+6+6+ (2-47)
29 式(2-42)和式(2-43)是两相异步电动机传递函数的两种不同形式,它们与直流电动机的传递函 数在形式上完全相同。 6.齿轮系 在许多控制系统中常用高转速、小转矩电动机来 组成执行机构,而负载通常要求低转速、大转矩进行 调整,需要引入减速器进行匹配。减速器一般是一个 齿轮组,它们在机械系统中的作用相当于电气系统中 的变压器。如图2-11所示,主动齿轮与从动齿轮的转 速和齿数分别用 1、Z1 和 2 ,Z2 表示。一级齿轮 的传动比定义为 1 2 2 1 1 Z Z i = = (2-44) 控制系统一般用减速齿轮系,故 i 1 1 。明显地,一级齿轮减速器的传递函数可写为 1 1 2 1 ( ) ( ) ( ) s i s G s = = (2-45) 为了考虑负载和齿轮系对电动机特性的影响,一般要将负载和齿轮系的力矩、转动惯量 以及黏滞摩擦折合到电动机轴上进行计算。依据牛顿定律列写电机轴上的力矩平衡方程,可 以导出折算到电动机轴上的转动惯量和黏滞摩擦系数分别为 2 2 1 1 1 J i J = J + 2 2 1 1 1 f i f = f + 对于多级齿轮系,折算到电机轴上的等效转动惯量和等效黏滞摩擦系数分别为 + = + + 3 2 1 2 2 2 1 1 ) 1 ) ( 1 ( J i i J i J J (2-46) + = + + 3 2 1 2 2 2 1 1 ) 1 ) ( 1 ( f i i f i f f (2-47)
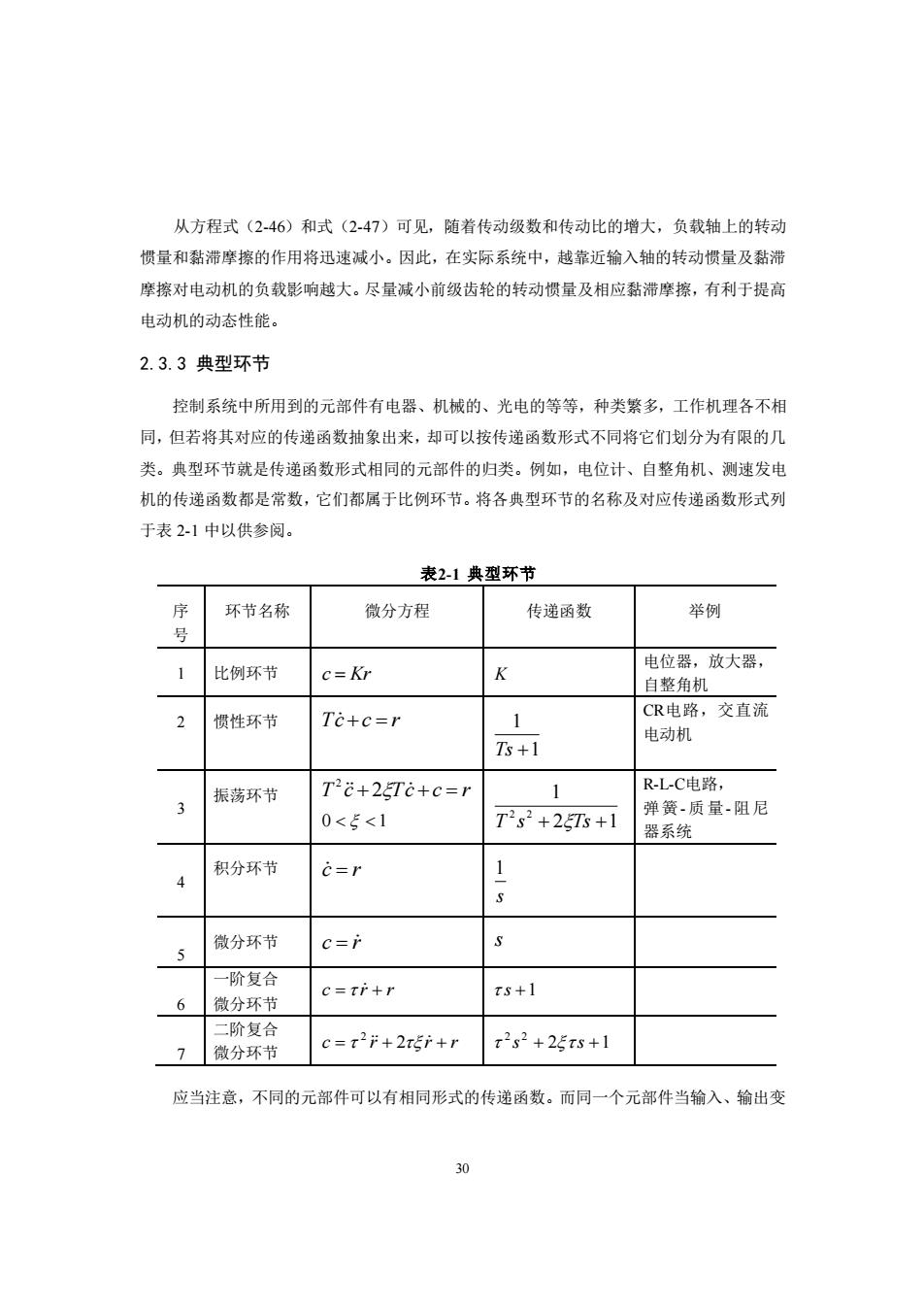
从方程式(2-46)和式(247)可见,随者传动级数和传动比的增大,负载轴上的转动 惯量和黏滞摩擦的作用将迅速减小。因此,在实际系统中,越靠近输入轴的转动惯量及黏滞 摩擦对电动机的负载影响越大。尽量减小前级齿轮的转动惯量及相应黏滞摩擦,有利于提高 电动机的动态性能。 2.3.3典型环节 控制系统中所用到的元部件有电器、机械的、光电的等等,种类繁多,工作机理各不相 同,但若将其对应的传递函数抽象出来,却可以按传递函数形式不同将它们划分为有限的几 类。典型环节就是传递函数形式相同的元部件的归类。例如,电位计、自整角机、测速发电 机的传递函数都是常数,它们都属于比例环节。将各典型环节的名称及对应传递函数形式列 于表2-1中以供参阅。 表21典型环节 序 环节名称 微分方程 传递函数 举例 1 比例环节 c=Kr K 电位器,放大器, 自整角机 2 惯性环节 Te+c=r CR电路,交直流 1 电动机 5+1 振荡环节 Tc+2Te+c=r 1 R-L-C电路, 3 0<E<1 T2s2+25T+1 弹簧-质量-阻尼 器系统 积分环节 c=r 1 4 微分环节 c=i 5 一价有合 c=Tr+r ts+l 微分环节 二阶复 c=T-i+2tEr+r x2s2+25xs+1 7微分环节 应当注意,不同的元部件可以有相同形式的传递函数。而同一个元部件当输入、输出变 0
30 从方程式(2-46)和式(2-47)可见,随着传动级数和传动比的增大,负载轴上的转动 惯量和黏滞摩擦的作用将迅速减小。因此,在实际系统中,越靠近输入轴的转动惯量及黏滞 摩擦对电动机的负载影响越大。尽量减小前级齿轮的转动惯量及相应黏滞摩擦,有利于提高 电动机的动态性能。 2.3.3 典型环节 控制系统中所用到的元部件有电器、机械的、光电的等等,种类繁多,工作机理各不相 同,但若将其对应的传递函数抽象出来,却可以按传递函数形式不同将它们划分为有限的几 类。典型环节就是传递函数形式相同的元部件的归类。例如,电位计、自整角机、测速发电 机的传递函数都是常数,它们都属于比例环节。将各典型环节的名称及对应传递函数形式列 于表 2-1 中以供参阅。 表2-1 典型环节 序 号 环节名称 微分方程 传递函数 举例 1 比例环节 c Kr = K 电位器,放大器, 自整角机 2 惯性环节 Tc +c = r 1 1 Ts + CR电路,交直流 电动机 3 振荡环节 T c + 2Tc + c = r 2 0 1 2 1 1 2 2 T s + Ts + R-L-C电路, 弹簧- 质量- 阻尼 器系统 4 积分环节 c = r s 1 5 微分环节 c = r s 6 一阶复合 微分环节 c = r + r s +1 7 二阶复合 微分环节 c = r + 2 r + r 2 2 1 2 2 s + s + 应当注意,不同的元部件可以有相同形式的传递函数。而同一个元部件当输入、输出变

量选择不同时,对应的传递函数一般不一样。 建立“典型环节”概念,便于我们分析系统。可以认为典型环节是构成系统传递函数的 最基本单元,任何系统的传递函数都可以看成是由典型环节组合而成的。 2.3.4传递函数的标准形式 传递函数通常表示成式(2-27)形式的有理分式,根据系统分析的需要,也常表示成首 1标准型或尾1标准型。 1.首1标准型(零、极点形式) 将传递函数(2-27)的分子、分母最高次项(首项)系数均化为1,表示为 KΠ(s-z,) G(s)= (2-48) Πs-p,) 的形式,称之为首1标准型:因式分解后也称为传递函数的零、极点形式。式(2-48)中, 三1,52,二m为传递函数分子多项式等于零的根,称为传递函数的零点:P1,P2,Pn为传 递函数分母多项式等于零的根,称为传递函数的极点。 2.尾1标准型(典型环节形式) 将传递函数(2-27)的分子、分母最低次项(尾项)系数均化为1,表示为 s+i(G32+25s+0 G(s)=K- (2-49 ,s+0Ts+2可,s+ 的形式,称之为尾1标准型(简称尾1型):因式分解后也称为传递函数的典型环节形式。 式(249)中每个因子都对应一个典型环节。这里,K称为系统增量。K与K‘的关系为 K'TEl K (2-50) Πp, 例2-7已知某传递函数为G(s)= 30(s+2 5(5+3s2+25+2)
31 量选择不同时,对应的传递函数一般不一样。 建立“典型环节”概念,便于我们分析系统。可以认为典型环节是构成系统传递函数的 最基本单元,任何系统的传递函数都可以看成是由典型环节组合而成的。 2.3.4 传递函数的标准形式 传递函数通常表示成式(2-27)形式的有理分式,根据系统分析的需要,也常表示成首 1 标准型或尾 1 标准型。 1.首 1 标准型(零、极点形式) 将传递函数(2-27)的分子、分母最高次项(首项)系数均化为 1,表示为 = = − − = n i i m j j s p K s z G s 1 1 * ( ) ( ) ( ) (2-48) 的形式,称之为首 1 标准型;因式分解后也称为传递函数的零、极点形式。式(2-48)中, m z ,z ,...,z 1 2 为传递函数分子多项式等于零的根,称为传递函数的零点; p p pn , ,..., 1 2 为传 递函数分母多项式等于零的根,称为传递函数的极点。 2.尾 1 标准型(典型环节形式) 将传递函数(2-27)的分子、分母最低次项(尾项)系数均化为 1,表示为 = = = = + + + + + + = 1 2 1 2 1 2 2 1 1 2 2 1 ( 1) ( 2 1) ( 1) ( 2 1) ( ) n j j j n i i m k l l m l k s T s T s T s s s s G s K v (2-49) 的形式,称之为尾 1 标准型(简称尾 1 型);因式分解后也称为传递函数的典型环节形式。 式(2-49)中每个因子都对应一个典型环节。这里, K 称为系统增量。 K 与 * K 的关系为 = = = n i i m j j p K z K 1 1 * (2-50) 例 2-7 已知某传递函数为 ( 3)( 2 2) 30( 2) ( ) 2 + + + + = s s s s s G s