
3.3二阶系统的时间响应及动态性能 3.3.1二阶系统传递函数标准形式及分类 常见二阶系统结构图如图3-6所示其中K,T为环节参数。系统闭环传递函数为 (S)=T3+s+K 化成标准形式 0)2 (6)=+250.5+ (首1型)(3-5) C() s(T8+1) 1 ()=Tg+2T5+1 (尾1型)(36) 图36常见二阶系统结构图 T 11 、O,分别称为系统的阻尼比和无阻尼自然频率,是二阶系统重要的特征参数。二阶 系统的首1标准型传递函数常用于时域分析中,频域分析时则常用尾1标准型。 二阶系统闭环特征方程为 D(s)=s2+2505+0片=0 其特征特征根为 a=-5@,±0,后- 若系统阻尼比5取值范围不同,则特征根形式不同,响应特性也不同,由此可将二阶系统分 类,见表33。 表3-3二阶系统(按阻尼比5)分类表 分类 特征根 特征根分布 模态 5>1 2=-50,±0nV52-l 即 e 过阻尼 etr 1
57 3.3 二阶系统的时间响应及动态性能 3.3.1 二阶系统传递函数标准形式及分类 常见二阶系统结构图如图 3-6所示其中 K ,T 为环节参数。系统闭环传递函数为 T s s K K s + + = 2 1 ( ) 化成标准形式 2 2 2 2 ( ) n n n s s s + + = (首 1 型) (3-5) 2 1 1 ( ) 2 2 + + = T s T s s (尾 1 型) (3-6) 式中, K T T 1 = , 1 1 T K T n = = , 1 1 2 1 KT = 。 、n 分别称为系统的阻尼比和无阻尼自然频率,是二阶系统重要的特征参数。二阶 系统的首 1 标准型传递函数常用于时域分析中,频域分析时则常用尾 1 标准型。 二阶系统闭环特征方程为 ( ) 2 0 2 2 D s = s + n s + n = 其特征特征根为 1 2 1,2 = −n n − 若系统阻尼比 取值范围不同,则特征根形式不同,响应特性也不同,由此可将二阶系统分 类,见表 3-3。 表 3-3 二阶系统(按阻尼比 )分类表 分类 特征根 特征根分布 模态 1 过阻尼 1 2 1,2 = −n n − t t e e 2 1

5=1 乙2=-0n e-ou 临界阻尼 leou 0) 系统单位阶跃响应的拉氏变换 C(s)=()R(s)=(s++)s 进行拉氏反变换,得出系统单位阶跃响应 e 120 (3-7) T
58 = 1 临界阻尼 1,2 = − n t t n n te e − − 0 1 欠阻尼 2 1,2 = −n jn 1− e t e t n t n t n n 2 2 cos 1 sin 1 − − − − = 0 零阻尼 n 1,2 = j t t n n cos sin 数学上,线性微分方程的解由特解和齐次微分方程的通解组成。通解由微分方程的特征 根决定,代表自由响应运动。如果微分方程的特征根是 1,2 , , n 且无重根,则把函 数 t e 1 , t e 2 , , t n e 称为该微分方程所描述运动的模态,也叫振型。 如果特征根中有多重根 ,则模态是具有 t te ,t 2 e t , 形式的函数。 如果特征根中有共轭复根 = j ,则其共轭复模态 t e ( +j) 与 t e ( −j) 可写成实函 数模态 e t t sin 与 e t t cos 。 每一种模态可以看成是线性系统自由响应最基本的运动形态,线性系统自由响应则是其 相应模态的线性组合。 3.3.2 过阻尼二阶系统动态性能指标计算 设过阻尼二阶系统的极点为 ( ) n T 1 1 2 1 1 = − = − − − ( ) n T 1 1 2 2 2 = − = − + − ( ) T1 T2 系统单位阶跃响应的拉氏变换 s T s T s C s s R s n 1 ( 1 )( 1 ) ( ) ( ) ( ) 1 2 2 + + = = 进行拉氏反变换,得出系统单位阶跃响应 1 1 ( ) 1 2 1 1 2 1 2 − + − = + − − T T e T T e h t T t T t t 0 (3-7)

过阻尼二阶系统单位阶跃响应是无振荡 的单调上升曲线。根据式(37),令T/T2取 不同值,可分别求解出相应的无量纲调节时间 【,/T,如图37所示。图中为参变量,由 20上1z 171 s2+25s+o2=(s+1VTs+1/T2) 可解出 6=1+g) 图3-7过阻尼二阶系统的调节时问特性 2T/T, 当T/T,(或5)很大时,特征根入=-1VT比入,=-1VT远离虚轴,模态很快 衰减为零,系统调节时间主要由入=-1/T对应的模态e心决定。此时可将过阻尼二阶系 统近似看作由入,确定的一阶系统,估算其动态性能指标。图37曲线体现了这一规律性。 >图3-7的绘制程序, Tb=0:T=0:t=0:0.01:50,T2=10 for i 1:length(T2) T1=T2(1):0.1*T2(i):20*T2(1) for j=1:length(T1) Tb=[Tb T1(j)/T2(i)] nun=[1/T1G)*T2(i)] den=[10/T1(6D+1/T2(i)1/(T1(G)*T2(i)]: y step(mum,den,t): for k=length(y):-1:1 if(abs(y(k)-1)>=0.05 Ts=[Tsk*0.01)/T1(j] break; end ab plot(Tb.Ts.'b-'):set(ab.'Linewidth'.1.5):grid x1bc(T1T2'),y1abe1CTs/T1'),tit1e(过阻尼二阶系统的调节时间特性): 16 例33某系统闭环传递函数)+105+16·计第系统的动态性能指标
59 过阻尼二阶系统单位阶跃响应是无振荡 的单调上升曲线。根据式(3-7),令 T1 T2 取 不同值,可分别求解出相应的无量纲调节时间 T1 t s ,如图 3-7 所示。图中 为参变量,由 2 ( 1 )( 1 ) 1 2 2 2 s + n s + n = s + T s + T 可解出 1 2 1 2 2 1 ( ) T T + T T = 当 T1 T2 (或 )很大时,特征根 2 = −1 T2 比 1 = −1 T1 远离虚轴,模态 T2 t e − 很快 衰减为零,系统调节时间主要由 1 = −1 T1 对应的模态 T1 t e − 决定。此时可将过阻尼二阶系 统近似看作由 1 确定的一阶系统,估算其动态性能指标。图 3-7 曲线体现了这一规律性。 例 3-3 某系统闭环传递函数 10 16 16 ( ) 2 + + = s s s ,计算系统的动态性能指标。 图 3-7 过阻尼二阶系统的调节时间特性
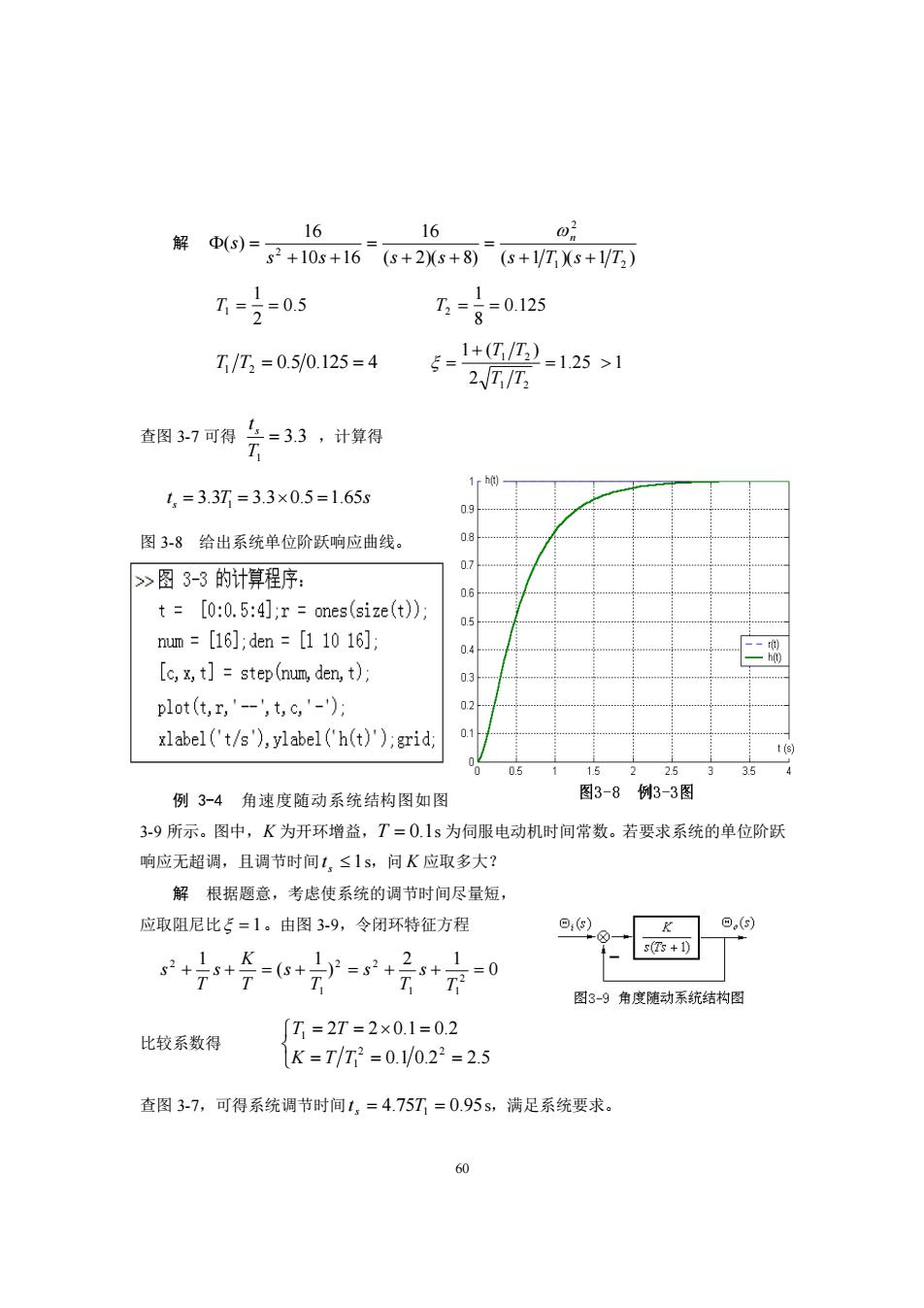
16 16 解)=+105+16s+2Xs+8)(s+VTX6+V四 T=2=05 7=g=0.125 T/T2=0.5/0.125=4 5=四=125>1 2、T/T 查图37可得兰33,计算得 1h 1.=3.3T=3.3×0.5=1.65s 09 图38给出系统单位阶跃响应曲线。 07 >图3-3的计算程序: 06 t=[0:0.5:4];r=ones(size(t)) 0.5 nm=[16]:den=[11016]: [c,x,t]=step(num,den,t); pl0t(t,x,'-',t,c,'-): xlabel('t/s'),ylabel('h(t)'):grid; 例3-4角速度随动系统结构图如图 图3-8例3-3图 3-9所示。图中,K为开环增益,T=0.1s为同服电动机时间常数。若要求系统的单位阶跃 响应无超调,且调节时间1,≤1s,问K应取多大? 解根据题意,考虑使系统的调节时间尽量短 应取阻尼比5=1。由图39,令闭环特征方程 图3-9角度随动系统结构图 [T-2T=2×0.1=0.2 比较系数得 K=T/T2=0.1/0.22=2.5 查图37,可得系统调节时间1,-4.75-0.95s,满足系统要求
60 解 ( 2)( 8) ( 1 )( 1 ) 16 10 16 16 ( ) 1 2 2 2 s s s s s T s T s n + + = + + = + + = 0.5 2 1 T1 = = 0.125 8 1 T2 = = T1 T2 = 0.5 0.125 = 4 1.25 1 2 1 ( ) 1 2 1 2 = + = T T T T 查图 3-7 可得 3.3 1 = T t s ,计算得 1 3.3 3.3 0.5 1.65 s t T s = = = 图 3-8 给出系统单位阶跃响应曲线。 例 3-4 角速度随动系统结构图如图 3-9 所示。图中, K 为开环增益, T = 0.1 s 为伺服电动机时间常数。若要求系统的单位阶跃 响应无超调,且调节时间 t s 1 s,问 K 应取多大? 解 根据题意,考虑使系统的调节时间尽量短, 应取阻尼比 = 1 。由图 3-9,令闭环特征方程 0 2 1 ) 1 ( 1 2 1 1 2 2 1 2 + + = + = + + = T s T s T s T K s T s 比较系数得 = = = = = = 0.1 0.2 2.5 2 2 0.1 0.2 2 2 1 1 K T T T T 查图 3-7,可得系统调节时间 t s = 4.75T1 = 0.95 s,满足系统要求

3.3.3欠阻尼二阶系统动态性能指标计算 1.欠阻尼二阶系统极点的两种表示方法 欠阻尼二阶系统的极点可以用如图3-0所示的两种形式表示。 (1)直角坐标表示 2=o±j04=-50n±jN1-50n(3-8 (2)“极”坐标表示 =o 「cosB=E sin B- (3-9) ∠1=B g=-0 2。欠阻尼二阶系统的单位阶跃响应 图3-10欠阻尼二阶系统颓点表示 由式(3-5),可得系统单位阶跃响应的拉氏变换为 1-1 s+25 C)=)o)=g+25@+m专s+5a,P+0-5@: s+50n 1-2on 系统单位阶跃响应为 0=1-ecos-gFa,小-三。ersm-EFa,j 1- i产2 -小gai-o小 i-京m-子o+arctan-E (3-10) 系统单位脉冲响应为 k0=h')=L户[Φ(s)]=L V1-5o. "年em-fa 0。 (3-11) 典型欠阻尼二阶系统的单位阶跃响应如图31所示。响应曲线位于两条包络线
61 3.3.3 欠阻尼二阶系统动态性能指标计算 1.欠阻尼二阶系统极点的两种表示方法 欠阻尼二阶系统的极点可以用如图 3-10 所示的两种形式表示。 (1)直角坐标表示 d n n j j 2 1,2 = = − 1− (3-8) (2)“极”坐标表示 = = n = − = 2 sin 1 cos (3-9) 2.欠阻尼二阶系统的单位阶跃响应 由式(3-5),可得系统单位阶跃响应的拉氏变换为 s s s C s s R s n n n 1 2 ( ) ( ) ( ) 2 2 2 + + = = 2 2 2 ( ) (1 ) 1 2 n n n s s s + + − + = − 2 2 2 2 2 2 2 2 ( ) (1 ) 1 ( ) (1 ) 1 1 n n n n n n s s s s + + − − − − + + − + = − 系统单位阶跃响应为 ( ) ( − ) = − = − − − − − h t e t e t n t n t n n 2 2 2 sin 1 1 ( ) 1 cos 1 − ( − )+ ( − ) = − − − t t e n n t n 2 2 2 2 1 cos 1 sin 1 1 1 2 2 2 1 1 sin 1 arctan 1 n t n e t − − − − + − (3-10) 系统单位脉冲响应为 − + + − − = = = − − 2 2 2 2 2 1 1 ( ) (1 ) 1 1 ( ) ( ) ( ) n n n n s k t h t L s L e t n n t n 2 2 sin 1 1 − − = − (3-11) 典型欠阻尼二阶系统的单位阶跃响应如图 3-11 所示。响应曲线位于两条包络线
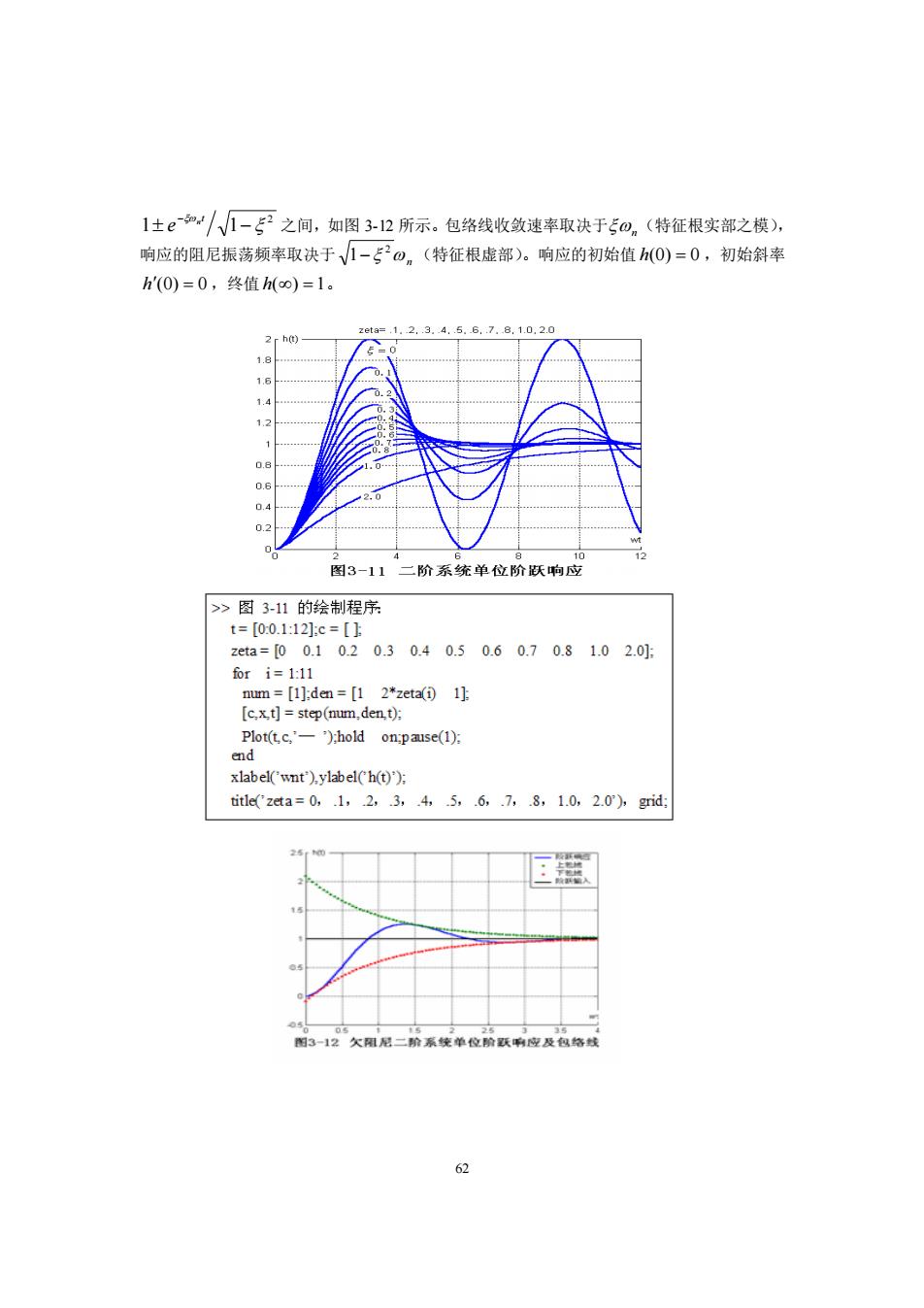
1±e/√1-2之间,如图32所示。包络线收敛速率取决于50。(特征根实部之模) 响应的阻尼振荡频率取决于√1-20。(特征根虚部)。响应的初始值h(0)=0,初始斜率 h'(0)=0,终值h(o)=1。 2.3.4.5.6.7.8,1.0 图3-11二阶系统单位阶跃响应 >图311的绘制程序 zta=00.1020.30.40.50.60.70.81.02.01 for i= ( xlabel('wnt).ylabel(h(t)); title'zeta=0,1,2,3,45,.6.7,8,1.0,2.0,gmid 一12欠阻尼二阶系饶单位跃响应及包
62 2 1 1 − − t n e 之间,如图 3-12 所示。包络线收敛速率取决于 n (特征根实部之模), 响应的阻尼振荡频率取决于 n 2 1− (特征根虚部)。响应的初始值 h(0) = 0 ,初始斜率 h(0) = 0 ,终值 h() = 1

>图3-12的绘制程序: m=2.5:zeta=0.4;te[0:0.05:4] t1 acos(zeta)*ones(1,length(t)). al =(1/sqrt(1-zeta"2)); hl 1-al*exp(-zeta*m*t).*sin(wn*sqrt(1-zeta"2)*t+t1); bu al*exp(-zetatwmn*t)+1;b1=2-bu; plot(t,hi,'-',t,bu,'.',t,bl,'.',t,ones(size(t)),'k-');grid xlabel('mt'),ylabel('h(t)'); 3 欠阻尼二阶系统动态性能指标计算 (1)峰值时间1。:令h)=k()=0,利用式(3-11)可得 snV1-5o,1=0 即有 V1-5201=0,π,2元,3π,… 由图3-1,并根据峰值时间定义,可得 ,-50 (3-12) (2)超调量σ%:将式(3-12)代入式(3-10)整理后可得 h(tp)=1+e a%-,)-Mox100%=e/Fx100% (3-13) h(co) 可见,典型欠阻尼二阶系统的超调量σ只与阻尼比5有关,两者的关系如图313所示
63 . 3 欠阻尼二阶系统动态性能指标计算 (1)峰值时间 p t :令 h(t) = k(t) = 0 ,利用式(3-11)可得 sin 1 0 2 − n t = 即有 1− 2 n t = 0, , 2, 3 , 由图 3-1,并根据峰值时间定义,可得 n p t 2 1− = (3-12) (2)超调量 0 0 :将式(3-12)代入式(3-10)整理后可得 2 1 ( ) 1 − − h t = + e p % 100 ( ) ( ) ( ) − = h h t p h % 2 − 1− = e 100 % (3-13) 可见,典型欠阻尼二阶系统的超调量 0 0 只与阻尼比 有关,两者的关系如图 3-13 所示
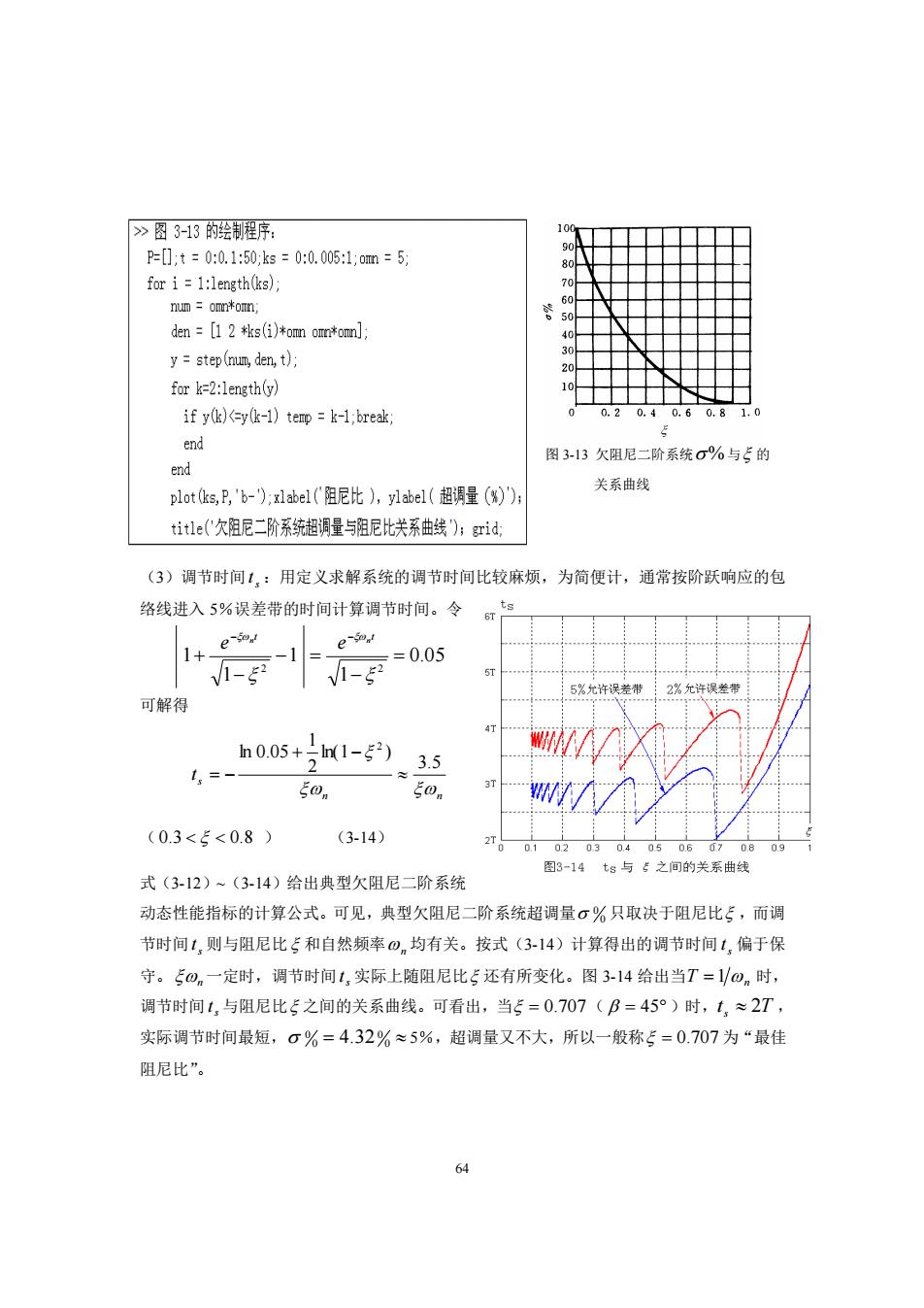
>图313的绘制程序: P=1;t=0:0.1:50,ks=0:0.005:1;om=5, fori=1:length(ks) den [1 2 *ks(i)tom omtom]: y=step(num,den,t); for k=2:length(y) if y(k)(=y(k-1)temp=k-1;break; 0.2 0.4 0.0.810 d end 图313欠阻尼二阶系统G%与5的 plot(ks,B,'b-):xlabel(阻尼比),ylabel(超调量(W)): 关系曲线 title('欠阻尼二阶系统超调量与阻尼北关系曲线):rid, (3)调节时间【,:用定义求解系统的调节时间比较麻烦,为简便计,通常按阶跃响应的包 络线进入5%误差带的时间计算调节时间。令研口 1+ -1 e 1- 5%允许误差带 允许误差 可解得 n0.05+ n(1-2) 3.5 1.=- 50n 0. 3T (0.3<5<0.8) (3-14) 图3-14t与4之间的类系曲绿 式(3-12)~(3-14)给出典型欠阻尼二阶系统 动态性能指标的计算公式。可见,典型欠阻尼二阶系统超调量。%只取决于阻尼比5,而调 节时间1,则与阻尼比5和自然频率,均有关。按式(3-14)计算得出的调节时间1,偏于保 守。o。一定时,调节时间1,实际上随阻尼比5还有所变化。图3-14给出当T=on时, 调节时间1,与阻尼比5之间的关系曲线。可看出,当5=0.707(B=45°)时,1,≈2T 实际调节时间最短,6%=4.32%≈5%,超调量又不大,所以一般称5=0.707为“最佳 阻尼比
64 图 3-13 欠阻尼二阶系统 % 与 的 关系曲线 (3)调节时间 s t :用定义求解系统的调节时间比较麻烦,为简便计,通常按阶跃响应的包 络线进入 5%误差带的时间计算调节时间。令 0.05 1 1 1 1 2 2 = − − = − + − − t t n n e e 可解得 n n s t 3.5 ln(1 ) 2 1 ln 0.05 2 + − = − ( 0.3 0.8 ) (3-14) 式(3-12)~(3-14)给出典型欠阻尼二阶系统 动态性能指标的计算公式。可见,典型欠阻尼二阶系统超调量 0 0 只取决于阻尼比 ,而调 节时间 s t 则与阻尼比 和自然频率 n 均有关。按式(3-14)计算得出的调节时间 s t 偏于保 守。 n 一定时,调节时间 s t 实际上随阻尼比 还有所变化。图 3-14 给出当 T =1 n 时, 调节时间 s t 与阻尼比 之间的关系曲线。可看出,当 = 0.707 ( = 45 )时, t s 2T , 实际调节时间最短, 0 0 = 4.320 0 5%,超调量又不大,所以一般称 = 0.707 为“最佳 阻尼比

>>图3-14程序 Ts2=0Ts5=0:Ks=0:sg1:t0.01:50: om om:don-[12mom num-sden.() 6800 end2.1 if abs(y(k)1))>=0.02 or k50-1 ifabs(v(k1))>=005 s5=[Ts5,k*0.01]:break en end end set(aa'Co1o「1111 ab=plot(Ks.Ts2.r.Ks.Ts5.b.):set(ab.LineWidth.2):grid: 4.典型欠阻尼二阶系统动态性能、系统参数及极点分布之间的关系 根据式(3-13、式(314)及式(3-8)、式(3-9),可以进一步讨论系统动态性能、系 统参数及闭环极点分布间的规律性。 当0,固定,5增加(B减小)时,系统极点在5平面按 图3-15中圆弧轨迹(1)移动,对应系统超调量σ%减小:同 时由于极点远离虚轴,o,增加,调节时间1,减小。图3-16(a 给出0,=1,5改变时的系统单位阶跃响应过程。 当5周定,o,增加时,系统极点在s平面按图3-15中的 射线轨迹(1)移动,对应系统超调量。%不变:由于极点远 离虚轴,50n增加,调节时间1,减小。图316b)给出了 图3-15系统极点轨迹 5=0.5(B=60°),0n变化时的系统单位阶跃响应过程
65 4.典型欠阻尼二阶系统动态性能、系统参数及极点分布之间的关系 根据式(3-13)、式(3-14)及式(3-8)、式(3-9),可以进一步讨论系统动态性能、系 统参数及闭环极点分布间的规律性。 当 n 固定, 增加( 减小)时,系统极点在 s 平面按 图 3-15 中圆弧轨迹(I)移动,对应系统超调量 %减小;同 时由于极点远离虚轴, n 增加,调节时间 s t 减小。图 3-16(a) 给出 n =1, 改变时的系统单位阶跃响应过程。 当 固定, n 增加时,系统极点在 s 平面按图 3-15 中的 射线轨迹(II)移动,对应系统超调量 %不变;由于极点远 离虚轴, n 增加,调节时间 s t 减小。图 3-16(b)给出了 =0.5( = 60 ),n 变化时的系统单位阶跃响应过程

一般实际系统中,T是系统的固定参数,不能随意改变,而开环增益K是各环节总的 for 0j=ones(seo0m=1sg=0.1,02,0.3,0.4,0.5,0.6,0.7,0.8 num=sg(i)"sg()tom*om;den=[1. set(.5)hold on 品en1sd06nef虚部=1极点实部(01,02,03,04050.6072,08》 grid;pase(2);clf for i=1:6 num =omn()*o den=[1,2*ks"omn(i)omn(i)omn(i) -.tc,b-) el)ate0ikkg=05自然须率0250512490 10j,=ones((se0sg=10m=0.2,0.5,0.70.8.0.9,12,3,5 for=1:9 mum=s*sgom(om():de=[1.sg.sg*sgtom()om(] set(ab LineWidth 1.5)hold on I",tc,b er1sd6n =1,极点嘘部(0.2,0.5,0.7,0.8,0.9,12,3,5) grid.pase(2) 传递系数,可以调节。K增大时,系统极点在s平面按图3-15中的垂直线()移动,阻 尼5变小,超调量。%会增加。图3-16(©)给出T=1,K变化时系统单位阶跃响应的过程
66 一般实际系统中, T 是系统的固定参数,不能随意改变,而开环增益 K 是各环节总的 传递系数,可以调节。 K 增大时,系统极点在 s 平面按图 3-15 中的垂直线(III)移动,阻 尼 变小,超调量 %会增加。图 3-16(c)给出 T = 1,K 变化时系统单位阶跃响应的过程