
3.2一阶系统的时间响应及动态性能 3.2.1一阶系统传递函数标准形式及单位阶跃响应 一阶系统的典型结构如图32所示,K是开环增益。 系统传递函数的标准形式(尾1型)为 图3-2一阶系统典型结构图 p(S)= +KT5+ (3-2) 式中T=VK称为一阶系统的时间常数,系统特征根1=-1/T。 系统单位阶跃响应的拉氏变换为 C(s)=D(s)-R(s)= 1111 Ts+1s ss+l/T 单位阶跃响应 h0=Lr[cs=1-e子 (3-3) 3.2.2一阶系统动态性能指标计算 一阶系统的单位阶跃响应如图33所示,响应 是单调的指数上升曲线。依调节时间1,的定义有 hl.)=1-e7=0.95 解得 1=37 (3-4) 时间常数T是一阶系统的重要特征参数。T越小, 系统极点越远离虚轴,过波过程越快。图3-4给出 图3-3一阶系统的单位阶跃响应 阶系统阶跃响应随时间常数T变化的趋势。 >》图3-4的绘图程序: t=[0:0.1:10]:T=1.0 -A for i 1:4 nmum三[01]:den=[i*灯1] [c,x,t]=step(num,den,t); plot(t,c,'k-); hold on ;pause(1); end;grid; 一阶系统阶跃响应随T变化的始势
57 3.2 一阶系统的时间响应及动态性能 3.2.1 一阶系统传递函数标准形式及单位阶跃响应 一阶系统的典型结构如图 3-2 所示, K 是开环增益。 系统传递函数的标准形式(尾 1 型)为 1 1 ( ) + = + = s K Ts K s (3-2) 式中 T =1 K 称为一阶系统的时间常数,系统特征根 = −1 T 。 系统单位阶跃响应的拉氏变换为 Ts s s s T C s s R s 1 1 1 1 1 1 ( ) ( ) ( ) + = − + = = 单位阶跃响应 T t h t L C s e − − ( ) = ( ) = 1− 1 (3-3) 3.2.2 一阶系统动态性能指标计算 一阶系统的单位阶跃响应如图 3-3 所示,响应 是单调的指数上升曲线。依调节时间 s t 的定义有 T t s s h t e − ( ) = 1− =0.95 解得 t s = 3T (3-4) 时间常数 T 是一阶系统的重要特征参数。 T 越小, 系统极点越远离虚轴,过渡过程越快。图 3-4 给出一 阶系统阶跃响应随时间常数 T 变化的趋势。 图 3-3 一阶系统的单位阶跃响应
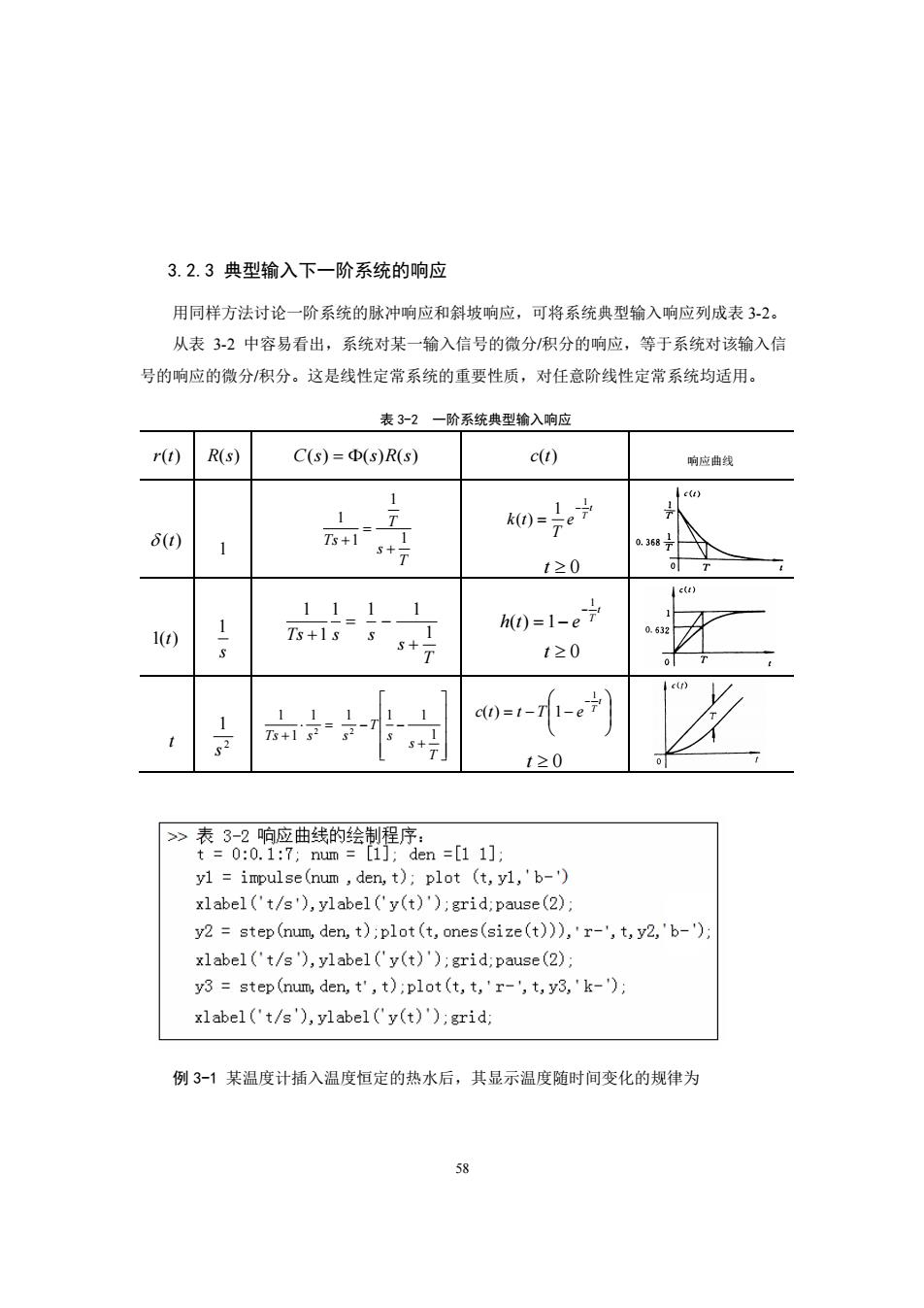
3.2.3典型输入下一阶系统的响应 用同样方法讨论一阶系统的脉冲响应和斜坡响应,可将系统典型输入响应列成表3-2。 从表32中容易看出,系统对某一输入信号的微分积分的响应,等于系统对该输入信 号的响应的微分积分。这是线性定常系统的重要性质,对任意阶线性定常系统均适用。 表子一2一阶系统典型输入响应 r(t)R(s) C(s)=(s)R(s) c(t) 响应鱼找 1 k0=子e7 6() 1 368于 t≥0 111 1 1() 1- Ts+15s s+ 0=1-e t20 c0=1-71-e7 1≥0 >表3-2响应曲线的绘制程序: t=0:0.1:7:m=[1]:den=[11]: y1 impulse(num,den,t);plot (t,y1,'b-') xlabel('t/s'),ylabel('y(t)'):grid:pause(2) y2 step(num,den,t):plot(t,ones(size(t))),'r-',t,y2,'b-') xlabel('t/s'),ylabel('y(t)');grid:pause(2) y3 step(num,den,t',t);plot (t,t,'r-',t,y3,'k-'); xlabel('t/s'),ylabel('y(t)'):grid; 例3-1某温度计插入温度恒定的热水后,其显示温度随时间变化的规律为 58
58 3.2.3 典型输入下一阶系统的响应 用同样方法讨论一阶系统的脉冲响应和斜坡响应,可将系统典型输入响应列成表 3-2。 从表 3-2 中容易看出,系统对某一输入信号的微分/积分的响应,等于系统对该输入信 号的响应的微分/积分。这是线性定常系统的重要性质,对任意阶线性定常系统均适用。 表 3-2 一阶系统典型输入响应 r(t) R(s) C(s) = (s)R(s) c(t) 响应曲线 (t) 1 T s T Ts 1 1 1 1 + = + t T e T k t 1 1 ( ) − = t 0 1(t) s 1 T s Ts s s 1 1 1 1 1 1 + = − + t T h t e 1 ( ) 1 − = − t 0 t 2 1 s + = − − + T s s T Ts s s 1 1 1 1 1 1 1 2 2 = − − − t T c t t T e 1 ( ) 1 t 0 例 3-1 某温度计插入温度恒定的热水后,其显示温度随时间变化的规律为
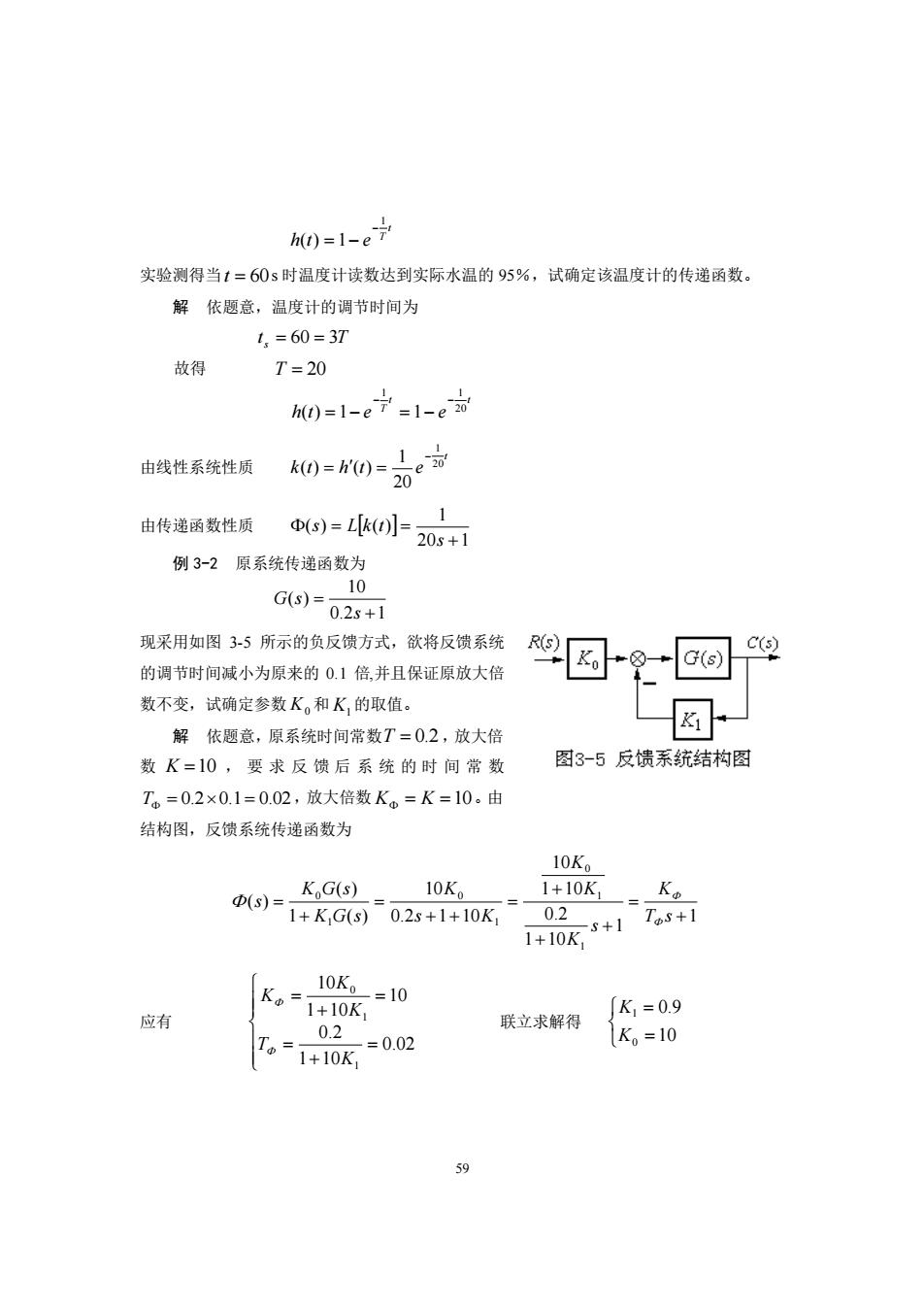
0=1-e户 实验测得当1=60s时温度计读数达到实际水温的95%,试确定该温度计的传递函数。 解依题意,温度计的调节时间为 1,=60=37 故得 T=20 m=l-e宁=l-e品 由线性系统性质 0=h0)=e动 20 Φ(s)=[k)]= 1 由传递函数性质 20s+1 例3-2原系统传递函数为 G6)=、10 0.2s+1 现采用如图3-5所示的负反馈方式,欲将反馈系统 R(s G(s) c 的调节时间减小为原来的0.1倍,并且保证原放大倍 数不变,试确定参数K。和K,的取值。 解依题意,原系统时间常数T=02,放大倍 数K=10,要求反馈后系统的时间常数 图3-5反馈系统结构图 Tw=0.2×0.1=0.02,放大倍数K。=K=10。由 结构图,反馈系统传递函数为 10K Φ(s)= KoG(s) 10Ko 1+10K Ko 1+KG(s)0.2s+1+10K 0.2 -s+1 Tos+1 1+10K Ko= 10K。=10 1+10K K1=0.9 应有 0.2一=0.02 联立求解得 Tw=1+10K K=10 59
59 t T h t e 1 ( ) 1 − = − 实验测得当 t = 60 s 时温度计读数达到实际水温的 95%,试确定该温度计的传递函数。 解 依题意,温度计的调节时间为 t s = 60 = 3T 故得 T = 20 t t T h t e e 20 1 1 ( ) 1 1 − − = − = − 由线性系统性质 t k t h t e 20 1 20 1 ( ) ( ) − = = 由传递函数性质 20 1 1 ( ) ( ) + = = s s L k t 例 3-2 原系统传递函数为 0.2 1 10 ( ) + = s G s 现采用如图 3-5 所示的负反馈方式,欲将反馈系统 的调节时间减小为原来的 0.1 倍,并且保证原放大倍 数不变,试确定参数 K0 和 K1 的取值。 解 依题意,原系统时间常数 T = 0.2 ,放大倍 数 K =10 , 要 求 反 馈 后 系 统 的 时 间 常 数 T = 0.20.1= 0.02 ,放大倍数 K = K =10 。由 结构图,反馈系统传递函数为 1 1 1 10 0.2 1 10 10 0.2 1 10 10 1 ( ) ( ) ( ) 1 1 0 1 0 1 0 + = + + + = + + = + = T s K s K K K s K K K G s K G s s 应有 = + = = + = 0.02 1 10 0.2 10 1 10 10 1 1 0 K T K K K 联立求解得 = = 10 0.9 0 1 K K