
第二章自动控制系统的数学描述 一、控制系统的数学模型 控制系统的数学模型是描述自动控制系统输入、输出以及内部各变量的静态和动态关系的数 学表达式。控制系统的数学模型有多种形式:代数方程、微分方程、传递函数、差分方程、 脉冲传递函数、状态方程、方框图、结构图、信号流图和静态励态关系表等。 控制系统的数学模型的求取,可采用解析法或实验法。系统的数学模型关系到整个系统地分 析和研究,建立合理的数学模型是分析和研究自动控制系统最重要的基础。 1.微分方程 用解析法建立系统的微分方程的步骤: 1) 确定系统的输入、输出变量: 2)根据系统的物理、化学等机理,依据列出各元件的输入、输出运动规律的动态方程: 3)消去中间变量,写出输入、输出变量的关系的微分方程。 2.传递函数 )定义:传递函数是在零初始条件下,系统(或环节)输出量的拉氏变换与输出量的 拉氏变换之比。 2)性质: a)传递函数是线性系统在复频域里的数学模型: b)传递函数只与系统本身的结构与参数有关,与输入量的大小和性质无关: ©)传递函数与微分方程有相通性,两者可以相互转换。 3)表达形式 设系统的动态方程为一个阶微分方程 doy()+a++a+ay=bor(m)+br(++b+br 其中:(n>m) 则系统的传递函数为: G6)=g-6s”+s-1++ RS)as”+as++an 传递函数也可写成分子、分母多项式因式分解的形式,即 G)==s+s+-s+).k+ RG+ps+P)5+p.)i+P,)
第二章 自动控制系统的数学描述 一、控制系统的数学模型 控制系统的数学模型是描述自动控制系统输入、输出以及内部各变量的静态和动态关系的数 学表达式。控制系统的数学模型有多种形式:代数方程、微分方程、传递函数、差分方程、 脉冲传递函数、状态方程、方框图、结构图、信号流图和静态/动态关系表等。 控制系统的数学模型的求取,可采用解析法或实验法。系统的数学模型关系到整个系统地分 析和研究,建立合理的数学模型是分析和研究自动控制系统最重要的基础。 1.微分方程 用解析法建立系统的微分方程的步骤: 1) 确定系统的输入、输出变量; 2) 根据系统的物理、化学等机理,依据列出各元件的输入、输出运动规律的动态方程; 3) 消去中间变量,写出输入、输出变量的关系的微分方程。 2.传递函数 1) 定义:传递函数是在零初始条件下,系统(或环节)输出量的拉氏变换与输出量的 拉氏变换之比。 2) 性质: a) 传递函数是线性系统在复频域里的数学模型; b) 传递函数只与系统本身的结构与参数有关,与输入量的大小和性质无关; c) 传递函数与微分方程有相通性,两者可以相互转换。 3) 表达形式 设系统的动态方程为一个 n 阶微分方程 ) ... ... ' 1 ( 1) 1 ( ) 0 ' 1 ( 1) 1 ( ) 0 n m a y a y a y a y b r b r b r b r m m m m n n n n + + + + = + + + − + − − − 其中:( 则系统的传递函数为: n n n m m m a s a s a b s b s b R s Y s G s + + + + + + = = − − ... ... ( ) ( ) ( ) 1 0 1 1 0 1 传递函数也可写成分子、分母多项式因式分解的形式,即 ( ) ( ) ( )( ) ( ) ( )( ) ( ) ( ) ( ) ( ) 1 1 1 2 1 2 j n j i m i n m s p k s z s p s p s p k s z s z s z R s Y s G s + + = + + + + + + = = = =
k-称为传递系数,k= a。 式中:-:,-分子多项式的根,又称为系统的零点 一P,一一分母多项式的根,又称为系统的极点 4)典型环节的传递函数 一个自动控制系统,可以认为是由一些典型环节(一些元件和部件)所组成。常见 的典型环节及其传递函数有以下几种: a)比例环节: b)积分环节: R(s)Ts c)微分环节:理想: 6得= 实际: G()=Y(s)=k.Ts R(s)1+Tas d)惯性环节: G)==k Rs1+T下 1 )二阶振荡环节 G=R87g+276++25g5+0 )迟延环节: ao-号 3.结构图(又称方框图,方块图) 1)结构图的基本形式(见图1.2-1) 8E(G R(s) C(s) B■ H(s) 结构图是反映系统各个元、部件的功能和信号流钢函解表示法,它是一种数学模 型。利用结构图可以求出系统的输入对输出的总的传递函数。在图1.21中 开环传递函数为:G,()=G6)H)=B9 E(s)
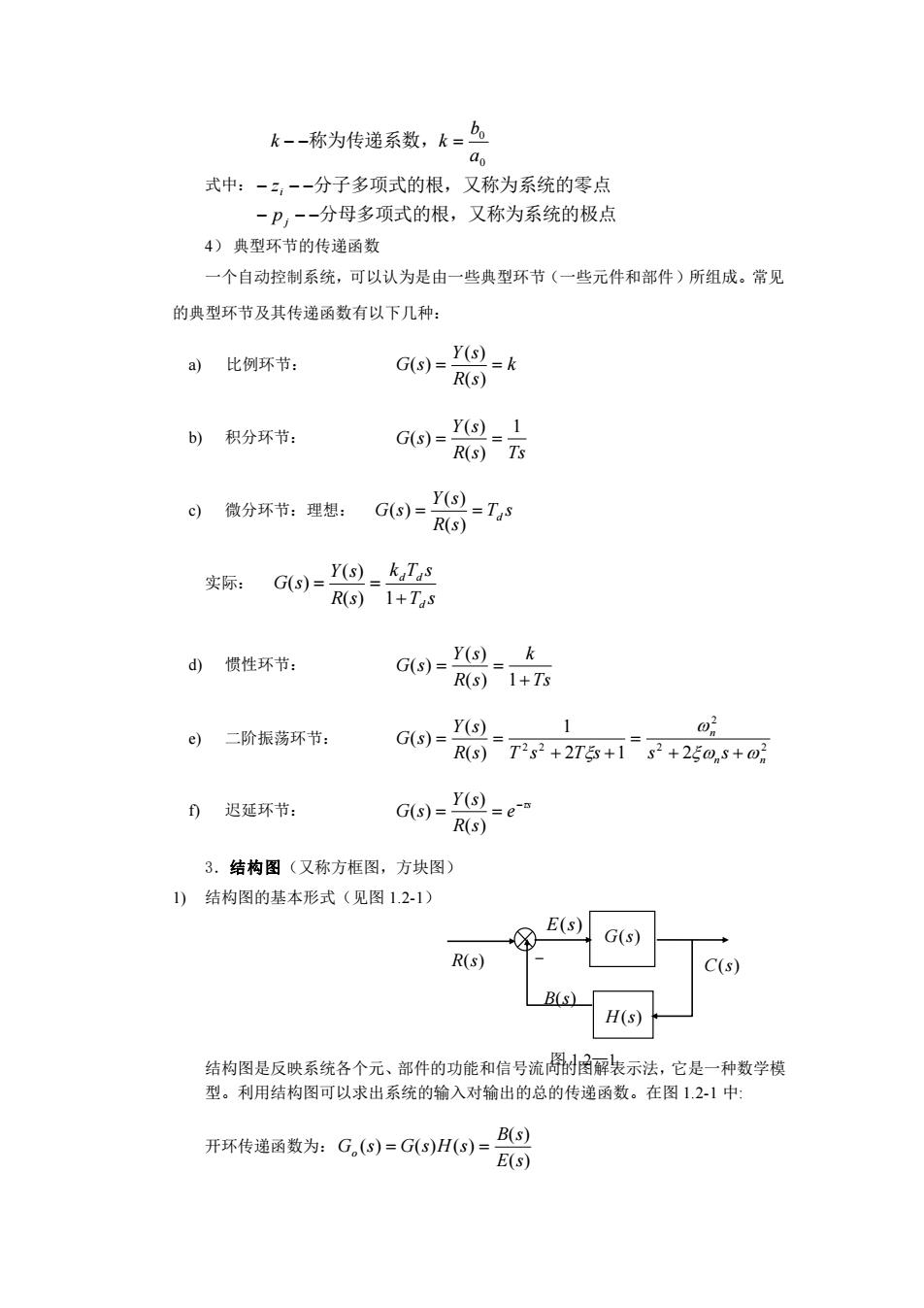
图 1.2—1 C(s) G(s) H(s) R(s) E(s) B(s) 式中: 分母多项式的根,又称为系统的极点 分子多项式的根,又称为系统的零点 称为传递系数, − − − − − − − − = j i p z a b k k 0 0 4) 典型环节的传递函数 一个自动控制系统,可以认为是由一些典型环节(一些元件和部件)所组成。常见 的典型环节及其传递函数有以下几种: a) 比例环节: k R s Y s G s = = ( ) ( ) ( ) b) 积分环节: R s Ts Y s G s 1 ( ) ( ) ( ) = = c) 微分环节:理想: T s R s Y s G s = = d ( ) ( ) ( ) 实际: T s k T s R s Y s G s d d d + = = ( ) 1 ( ) ( ) d) 惯性环节: Ts k R s Y s G s + = = ( ) 1 ( ) ( ) e) 二阶振荡环节: 2 2 2 2 2 2 1 2 1 ( ) ( ) ( ) n n n R s T s T s s s Y s G s + + = + + = = f) 迟延环节: s e R s Y s G s − = = ( ) ( ) ( ) 3.结构图(又称方框图,方块图) 1) 结构图的基本形式(见图 1.2-1) 结构图是反映系统各个元、部件的功能和信号流向的图解表示法,它是一种数学模 型。利用结构图可以求出系统的输入对输出的总的传递函数。在图 1.2-1 中: 开环传递函数为: ( ) ( ) ( ) ( ) ( ) E s B s G s G s H s o = =
闭环传递函数为:G,(句=1+G.间1+GHGR可 G(s) G(s)C(s) 2)结构图的等效变换基本法则: a)串联(如图1.2-2所示) R(s) C(s) G,(s) G(s) 图1.2-2 C(s) G(s)= =G,(s)G2(s) R(s) b)并联(如图1.2-3所示) G(s) C(s) R(s) G,(s) 图1.2-3 6o-8-G+6,o c)反馈联接(如图121所示) G,()=C)Gs) R(s)1±Gs) 上式分母中的”生”号为:当负反馈时,为“+”号,当正反馈时,为“-”号。 4.信号流图 信号流图是结构图的一种简易画法,它与结构图在本质上没有什么区别。只是形式 上的不同。 信号流图中的有关术语:源节点,阱节点,混合节点,前向通路,回路,不接触回 路
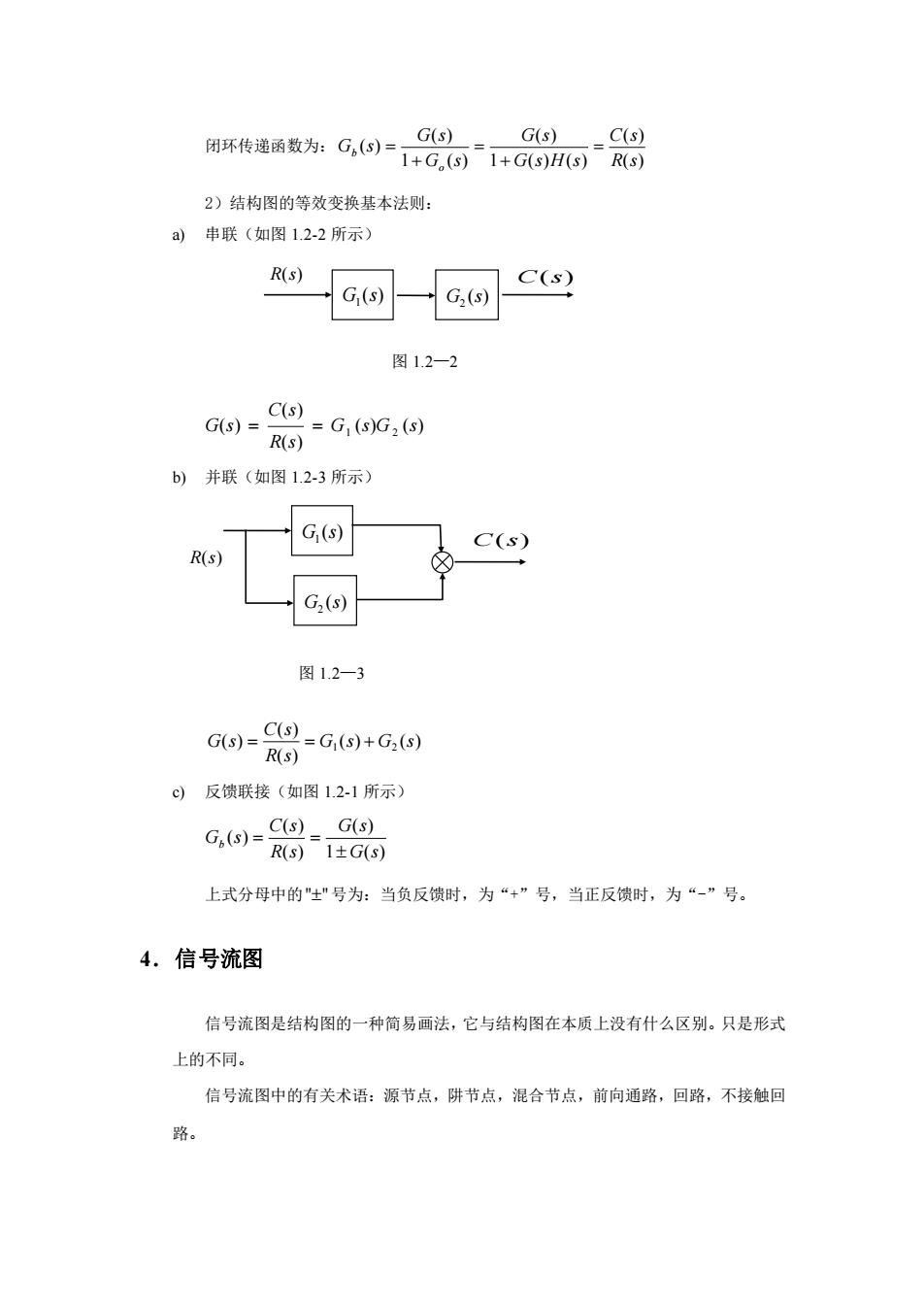
( ) 1 G s ( ) 2 G s R(s) C(s) 图 1.2—2 ( ) 1 G s ( ) 2 G s C(s) R(s) 图 1.2—3 闭环传递函数为: ( ) ( ) 1 ( ) ( ) ( ) 1 ( ) ( ) ( ) R s C s G s H s G s G s G s G s o b = + = + = 2)结构图的等效变换基本法则: a) 串联(如图 1.2-2 所示) ( ) ( ) ( ) ( ) ( ) 1 2 G s G s R s C s G s = = b) 并联(如图 1.2-3 所示) ( ) ( ) ( ) ( ) ( ) 1 2 G s G s R s C s G s = = + c) 反馈联接(如图 1.2-1 所示) 1 ( ) ( ) ( ) ( ) ( ) G s G s R s C s G s b = = 上式分母中的 "" 号为:当负反馈时,为“+”号,当正反馈时,为“-”号。 4.信号流图 信号流图是结构图的一种简易画法,它与结构图在本质上没有什么区别。只是形式 上的不同。 信号流图中的有关术语:源节点,阱节点,混合节点,前向通路,回路,不接触回 路

5.梅逊(Mason)公式 应用梅逊公式可以不经任何结构变换,一步写出系统的总的传递函数,所以是一个 十分有用的数学工具。梅逊公式如下: ao-器-2na 式中:△-特征式,△=1-∑L+∑LL。-∑LLL.+… n一从输入节点到输出节点前向通路的总条数 P一从输入节点到输出节点第k条前向通路总传递函数 ∑L。-所有不同回路的传递函数之和 ∑LL。-所有两两互不接触回路的传递函数乘积之和 ∑L.L,L,-所有三个互不接触回路的传递函数乘积之和 △4-与第k条前向通路不接触部分的△值
5.梅逊(Mason)公式 应用梅逊公式可以不经任何结构变换,一步写出系统的总的传递函数,所以是一个 十分有用的数学工具。梅逊公式如下: = = = n k pk k R s C s G s 1 1 ( ) ( ) ( ) 式中: −特征式, =1−La +LaLb −LaLbL c + 与第 条前向通路不接触部分的 值 所有三个互不接触回路的传递函数乘积之和 所有两两互不接触回路的传递函数乘积之和 所有不同回路的传递函数之和 从输入节点到输出节点第 条前向通路总传递函数 从输入节点到输出节点前向通路的总条数 − − − − − − k L L L L L L p k n k c a b a b a k