
自动控制原理 第五章 线性系统的频域分析 电子信息学院 主讲:张永韡博士讲师 email:ywzhangajust.edu.cn 口·4①,4二¥4三里0Q 第五章线性系统的域分析 自动控制膜理 电子信息学院11118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 自动控制原理 第五章 线性系统的频域分析 电子信息学院 主讲:张永韡 博士 讲师 email: ywzhang@just.edu.cn 第五章 线性系统的频域分析 自动控制原理 电子信息学院 1 / 118
主要内容 频率特性的基本概念 。频率特性G(d)的定义 ·频率特性G(jd)的图解表示 对数频率特性(Bode图)】 。典型环节的Bode图 ·开环系统对数频率特性(Bode) ③幅相频率特性(Nyquist图) ●典型环节的幅相频率特性 。系统开环幅相曲线 频域稳定判据 。幅角原理 。奈奎斯特稳定判据 。对数稳定判据 稳定裕度 ·稳定裕度的定义 。稳定裕度的计算 1口。t,花¥三至分0C 第五章线性系统的过分折 自动控制膜理 电子信息学院21118
. .. .. . . .. .. .. . . .. .. .. . . .. .. .. . . .. . . .. .. . 主要内容 1 频率特性的基本概念 频率特性 G ( jω ) 的定义 频率特性 G ( j ω ) 的图解表示 2 对数频率特性(Bode 图) 典型环节的 Bode 图 开环系统对数频率特性 ( Bode) 3 幅相频率特性(Nyquist 图) 典型环节的幅相频率特性 系统开环幅相曲线 4 频域稳定判据 幅角原理 奈奎斯特稳定判据 对数稳定判据 5 稳定裕度 稳定裕度的定义 稳定裕度的计算 6 利用开环频率特性分析系统的性能 7 利用闭环频率特性分析系统的性能 用向量法求闭环频率特性 闭环频率特性的几个特征量 第五章 线性系统的频域分析 自动控制原理 电子信息学院 2 / 118

线性系统的频域分析 频域分析法特点 (A)研究稳态正弦响应的幅值和相角随频率的变化规律 (B)由开环频率特性研究闭环稳定性及性能 (C)图解分析法,简单形象,有一定的近似性 (D)物理意义明确,许多元部件都可用实验法确定 (E)在校正方法中,频率法校正最为方便 口·40,立,1三,至分QC 第五章线性系统的域分析 自动控制膜理 电子信息学院3/118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 线性系统的频域分析 频域分析法特点 (A) 研究稳态正弦响应的幅值和相角随频率的变化规律 (B) 由开环频率特性研究闭环稳定性及性能 (C) 图解分析法,简单形象,有一定的近似性 (D) 物理意义明确,许多元部件都可用实验法确定 (E) 在校正方法中,频率法校正最为方便 第五章 线性系统的频域分析 自动控制原理 电子信息学院 3 / 118

主要内容 ©频率特性的基本概念 e对数频率特性(Bode图) O幅相频率特性(Nyquist图) Nyquist稳定性判据 稳定裕度 ⊙利用频率特性分析系统的性能 1口。t,花4三至分0C 第五章线性系统的过分折 自动控制膜理 电子信息学院041118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 主要内容 1 频率特性的基本概念 2 对数频率特性(Bode 图) 3 幅相频率特性(Nyquist 图) 4 Nyquist 稳定性判据 5 稳定裕度 6 利用频率特性分析系统的性能 第五章 线性系统的频域分析 自动控制原理 电子信息学院 4 / 118

期率特性的基本根念 频率特性的基本概念 例1RC电路如图所示,u,(t)=Asinwt,,求uc(t)=? Uc(s) 1 T-CR 1 G(s)= 1/T R U(s) CRs+1 Ts+1s+1/T 1/T Aw Co Uc(s)= C1s+C2 8+1/Ts2+w2 8+1/7+ s2+w2 Aw/T AwT C= lim s-1/Ts2+w2 1+w2T2 -AwT Aw C1= 1+w2T2 C2= 1+w2T2 U()=‘+ A V1+w2T2 uc(t)= sinwt.cos a-coswtsin al A sin(t-arctanw T) A 第五章线性系统的域分析 自动控制膜理 电子信息学院51118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 频率特性的基本概念 频率特性的基本概念 i R ur C uc 1 ωT √ 1 + ω2T2 α 例 1 RC 电路如图所示,ur(t) = A sin ωt, 求 uc(t) =? G(s) = Uc(s) Ur(s) = 1 CRs + 1 T=CR ====== 1 Ts + 1 = 1/T s + 1/T Uc(s) = 1/T s + 1/T · Aω s 2 + ω2 = C0 s + 1/T + C1s + C2 s 2 + ω2 C0 = lim s→−1/T Aω/T s 2 + ω2 = AωT 1 + ω2T2 C1 = −AωT 1 + ω2T2 C2 = Aω 1 + ω2T2 Uc(s) = AωT 1+ω2T2 · 1 s+1/T + √ A 1+ω2T2 [ √ 1 1+ω2T2 · ω s 2+ω2 − √ Tω 1+ω2T2 · s s 2+ω2 ] uc(t) = AωT 1+ω2T2 e −t T + √ A 1+ω2T2 [sin ωt · cos a − cos ωtsin a] = AωT 1+ω2T2 e −t T + √ A 1+ω2T2 sin(ωt − arctan ωT) 第五章 线性系统的频域分析 自动控制原理 电子信息学院 5 / 118
羧率特性的基本根念 频率特性G()的定义 接下来. 频率特性的基本概念 。频率特性G()的定义 G)的图解表示 对数频率特性(Bode图) 。典型环节的Boe图 。开环系统对数频率特件(Bode 幅相频率特性(Nyquist图)】 。典型环节的幅相频率特性 系统开环幅相曲线 频域稳定判据 。幅角原理 。奈奎斯特稳定判据 对数稳定判据 稳定裕度 。稳定裕度的定义 。稳定裕度的计算 1口。t,花¥三至分0C 第五章线性系统的过分折 自动控制原理 电子信息学院61118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 频率特性的基本概念 频率特性 G(jω) 的定义 接下来... 1 频率特性的基本概念 频率特性 G(jω) 的定义 频率特性 G(jω) 的图解表示 2 对数频率特性(Bode 图) 典型环节的 Bode 图 开环系统对数频率特性 ( Bode) 3 幅相频率特性(Nyquist 图) 典型环节的幅相频率特性 系统开环幅相曲线 4 频域稳定判据 幅角原理 奈奎斯特稳定判据 对数稳定判据 5 稳定裕度 稳定裕度的定义 稳定裕度的计算 6 利用开环频率特性分析系统的性能 7 利用闭环频率特性分析系统的性能 用向量法求闭环频率特性 闭环频率特性的几个特征量 第五章 线性系统的频域分析 自动控制原理 电子信息学院 6 / 118

期率特性的基本根念 频率特性G()的定义 频率特性G(w)的定义 A Cs(t)= sin(wt-arctanwT) 1tGa)川 幅频特性 0 Gw)定义一:GG)=|Gjw)川∠Gjw) ∠Gw)d 1c0o1=0=7示 相频特性° ∠Gjw)=∠cs(t)-∠rt)=arctanwT -90° G)定义二:G0w)=G(s)ls=jw 1 1 V1+w2T严 G0)定义三:G()= Cjw】 口4得,4二4三至OQ0 第五章线性系统的域分析 自动控制膜理 电子信息学院71118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 频率特性的基本概念 频率特性 G(jω) 的定义 频率特性 G(jω) 的定义 ω 0 1 |G(jω)| 幅频特性 ω −90◦ 0 ◦ ∠G(jω) 相频特性 cs(t) = A √ 1 + ω2T2 sin(ωt − arctan ωT) G { (jω) 定义一:G(jω) = |G(jω)|∠G(jω) |G(jω)| = |cs(t)| |r(t)| = √ 1 1+ω2T2 ∠G(jω) = ∠cs(t) − ∠r(t) = arctan ωT G(jω) 定义二:G(jω) = G(s)|s=jω 1 √ 1 + ω2T2 ∠−arctan ωT = | 1 1 + jωT |∠ 1 1 + jωT = 1 1 + jωT = 1 Ts + 1 |s=jω G(jω) 定义三:G(jω) = C(jω) R(jω) 第五章 线性系统的频域分析 自动控制原理 电子信息学院 7 / 118

羧率特性的基本根念 频率特性G()的定义 频率特性G(w)的定义 例2系统结构图如图所示, r(t)=3sin(2t+30),求c(t)。 解: e 1 Φ(s)= 母+令(创=1+ 训=l=e学方=0=6 3 ∠ΦGjw)=-arctanw2-63.4°=Lc.(d-∠r)=Lcs()-30° lc(训=号 ∠cs(t)=-63.4°+30°=-33.4° sim(2t-3.4) 3 c()= 日1,4之1年:)0C 第五章线性系统的过分折 自动控制膜理 电子信息学院81118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 频率特性的基本概念 频率特性 G(jω) 的定义 频率特性 G(jω) 的定义 r e 1 s c − 例 2 系统结构图如图所示, r(t) = 3 sin(2t + 30◦ ),求 cs(t)。 解: Φ(s) = 1 s + 1 ⇒ Φ(jω) = 1 1 + jω { |Φ(jω)| = | 1 1+jω | = √ 1 1+ω2 ω=2 = √ 1 5 = |cs(t)| |r(t)| = |cs(t)| 3 ∠Φ(jω) = − arctan ω ω=2 = −63.4 ◦ = ∠cs(t) − ∠r(t) = ∠cs(t) − 30◦ { |cs(t)| = √ 3 5 ∠cs(t) = −63.4 ◦ + 30◦ = −33.4 ◦ cs(t) = 3 √ 5 sin(2t − 33.4 ◦ ) 第五章 线性系统的频域分析 自动控制原理 电子信息学院 8 / 118
期率特性的基本根念 频率特性G6)的国解表示 接下来. 频率特性的基本概念 。店特性 G)的定义 。7 频率特性Gjd)的图解表示 2 对数频率特性(Bode图)】 。典型环节的Bode图 。开 数频率特性 Bode) 幅相频率特性(Nyquist图) 。典型环节的幅相频 系统开环幅相曲线 4 频域稳定判据 。幅角原理 。奈奎斯特稳定判据 。对数稳定判据 稳定裕度 0 稳定裕度的定义 。稳定裕度的计算 第五章线性系统的域分析 自动控制膜理 电子信息学院91118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 频率特性的基本概念 频率特性 G(jω) 的图解表示 接下来... 1 频率特性的基本概念 频率特性 G(jω) 的定义 频率特性 G(jω) 的图解表示 2 对数频率特性(Bode 图) 典型环节的 Bode 图 开环系统对数频率特性 ( Bode) 3 幅相频率特性(Nyquist 图) 典型环节的幅相频率特性 系统开环幅相曲线 4 频域稳定判据 幅角原理 奈奎斯特稳定判据 对数稳定判据 5 稳定裕度 稳定裕度的定义 稳定裕度的计算 6 利用开环频率特性分析系统的性能 7 利用闭环频率特性分析系统的性能 用向量法求闭环频率特性 闭环频率特性的几个特征量 第五章 线性系统的频域分析 自动控制原理 电子信息学院 9 / 118
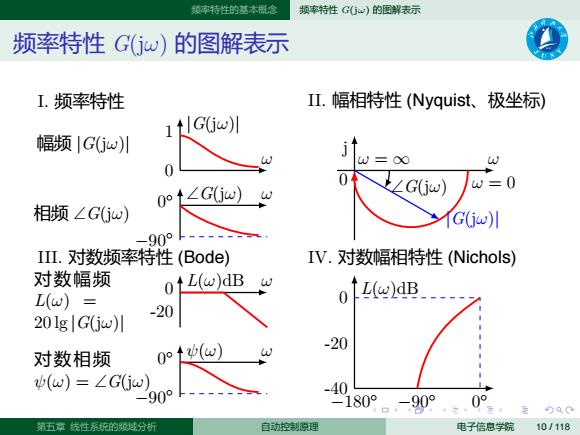
赖率特性的基本报念 频率特性G省)的图解表示 频率特性G(jw)的图解表示 I.频率特性 IⅡ.幅相特性(Nyquist、, 极坐标) 1tG0w川 幅频Gjw川 4G0w) w=0 0° ∠Giw) 相频∠GGw) Gjw)川 -90° III.对数频率特性(Bode) IV.对数幅相特性(Nichols) 对数幅频 o↑L(w)dB L(w)= ofL(ce)dB 201g|Gjw)川 -20 -20 对数相频 0t() (w)=∠Gj -90° -40 180°.-90° 0° 至)只0 第五章线性系统的过分折 自动控制膜理 电子信息学院101118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 频率特性的基本概念 频率特性 G(jω) 的图解表示 频率特性 G(jω) 的图解表示 I. 频率特性 ω 0 1 |G(jω)| 幅频 |G(jω)| ω −90◦ 0 ◦ ∠G(jω) 相频 ∠G(jω) II. 幅相特性 (Nyquist、极坐标) ω = ∞ ω 0 ω = 0 j |G(jω)| ∠G(jω) III. 对数频率特性 (Bode) ω -20 0 对数幅频 L(ω)dB L(ω) = 20 lg |G(jω)| ω −90◦ 0 ◦ ψ(ω) 对数相频 ψ(ω) = ∠G(jω) IV. 对数幅相特性 (Nichols) −180◦ −90◦ 0 ◦ -40 -20 0 L(ω)dB 第五章 线性系统的频域分析 自动控制原理 电子信息学院 10 / 118