
数据的处理 参考书:分析化学 第一部分:偏差 1.样本平均值 2.极差:表示数据的分散程度 R=Xmax -Xmin 3.偏差:X一X 4.平均偏差 平均偏差又称算术平均偏差,用来表示一组数据的精密度 平均偏差: d=∑x-=∑a 相对平均偏差: d dr==×100% X
i x n x 1 max min R x x 2. 极差: 表示数据的分散程度 1. 样本平均值 数据的处理 4. 平均偏差 平均偏差又称算术平均偏差,用来表示一组数据的精密度 平均偏差: i di n x x n d 1 1 相对平均偏差: 100% x d dr 第一部分:偏差 参考书:分析化学 x x 3. 偏差: i

例:测定某HC1与Na0H溶液的体积比。4次测定结果分别为:1.001, 1.005,1.000,1.002。计算平均偏差和相对平均偏差。 解:样本平均值:x=,∑x=41.001+1.05+1.00+102)=1.02 平均偏差: a=,∑X-X=1.001-1.002+1.005-1.002+1.000-1.002+1.002-1.002y =0.002 相对平均偏差:dr=(d/x)×100%=0.002/1.002×100%=0.2% 平均偏差和相对平均偏差表示精密度:越小越好
例: 测定某HCl与NaOH溶液的体积比。4次测定结果分别为:1.001, 1.005,1.000,1.002。计算平均偏差和相对平均偏差。 解: (1.001 1.005 1.000 1.002) 1.002 4 1 1 xi n x (1.001 1.002 1.005 1.002 1.000 1.002 1.002 1.002) 4 1 1 X X n d i =0.002 dr (d / x)100% 0.002 /1.002100% 0.2% 样本平均值: 平均偏差: 相对平均偏差: 平均偏差和相对平均偏差表示精密度: 越小越好

平均偏差和相对平均偏差表示精密度:越小越好 特点:简单 缺点:大偏差得不到应有反映 例:甲d, +0.3,-0.2,-0.4,+0.2,+0.1,+0.4,0.0,-0.3,+0.2,-0.3 乙d0.0,+0.1,-0.7,+0.2,-0.1,-0.2,+0.5,-0.2,+0.3,+0.1 平均偏差 :a=∑a=0.24 a2=∑4=0.24 精密度:甲比乙好,但二者平均偏差相同 可见:大偏差得不到应有反映
平均偏差和相对平均偏差表示精密度: 越小越好 特点:简单 缺点:大偏差得不到应有反映 例:甲di +0.3,-0.2,-0.4,+0.2,+0.1,+0.4,0.0,-0.3,+0.2,-0.3 乙di 0.0,+0.1,-0.7,+0.2,-0.1,-0.2,+0.5,-0.2,+0.3,+0.1 0.24 1 di n d 甲 0.24 1 di n d 乙 精密度:甲比乙好 ,但二者平均偏差相同 可见:大偏差得不到应有反映 平均偏差:

4.标准偏差 有限测定次数— 样本的标准偏差 (1)标准偏差: Σ-_d n-1 n-1 (2)相对标准偏差 (变异系数) CV=s/x×100%
4. 标准偏差 1 1 2 2 n d n x x s i i (2) 相对标准偏差 (变异系数) : 有限测定次数——样本的标准偏差 CV s/ x100% (1)标准偏差 :

如前面的例子: 甲d1:+0.3,-0.2,-0.4,+0.2,+0.1,+0.4,0.0,-0.3,+0.2,-0.3 乙d:0.0,+0.1,-0.7,+0.2,-0.1,-0.2,+0.5,-0.2,+0.3,+0.1 可以得到 1.甲:n=10 平均偏差:d甲=0.24 标准偏差:5甲=0.28 2.乙:n=10 平均偏差:d2=0.24 标准偏差:S乙=0.33 甲=t2比较不出结果 S甲<Sz 甲的精密度好于乙的精密度 用标准偏差比用平均偏差更科学更准确
如前面的例子: 甲di: +0.3,-0.2,-0.4,+0.2,+0.1,+0.4,0.0,-0.3,+0.2,-0.3 乙di: 0.0,+0.1,-0.7,+0.2,-0.1,-0.2,+0.5,-0.2,+0.3,+0.1 可以得到 1.甲: n=10 平均偏差 : d甲=0.24 标准偏差 : s甲=0.28 2.乙: n=10 平均偏差: d乙=0.24 标准偏差 : s乙=0.33 d甲=d乙 比较不出结果 s甲< s乙 甲的精密度好于乙的精密度 用标准偏差比用平均偏差更科学更准确
第二部分有效数字及其运算规则 2.1有效数字(significant figure)及其位数 1.实验过程中常遇到两类数字: (1)数目:如测定次数;倍数;系数;分数 (2)测量值或由测量值得到的计算值:数据的位数与测定准确 度有关.这类数字不仅表示数量的大小,而且要正确地反映测量 的精确程度—有效数字 2.有效数字的位数 结果 绝对误差 相对误差 有效数字位数 0.51800 ±0.00001 ±0.002% 5 0.5180 ±0.0001 ±0.002% 4 0.518 ±0.001 ±0.2% 3 0.0518 ±0.0001 ±0.2% 3 0.5018 ±0.0001 ±0.02% 4 0.5018% ±0.0001% ±0.0002% 4
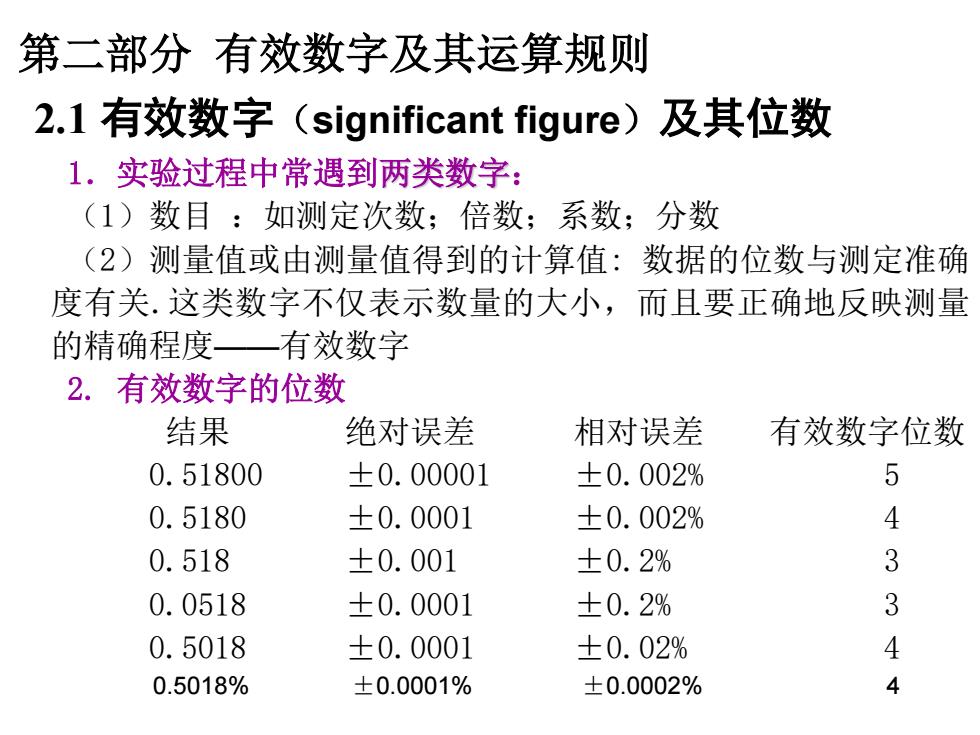
1.实验过程中常遇到两类数字: (1)数目 :如测定次数;倍数;系数;分数 (2)测量值或由测量值得到的计算值: 数据的位数与测定准确 度有关.这类数字不仅表示数量的大小,而且要正确地反映测量 的精确程度——有效数字 2. 有效数字的位数 结果 绝对误差 相对误差 有效数字位数 0.51800 ±0.00001 ±0.002% 5 0.5180 ±0.0001 ±0.002% 4 0.518 ±0.001 ±0.2% 3 0.0518 ±0.0001 ±0.2% 3 0.5018 ±0.0001 ±0.02% 4 0.5018% ±0.0001% ±0.0002% 4 2.1 有效数字(significant figure)及其位数 第二部分 有效数字及其运算规则

注意:1)分数、比例系数、实验次数、常数(如:π)等不记位数 2)pH计算,[H]=5.02x10-3 pH=2.299 有效数字按小数点后的位数计算 如:pH=11.058 3)误差、偏差及相对偏差,一般只保留一位有效数字 4)改变单位,不改变有效数字的位数: 如: 24.01mL 24.01×10-3L 5)第1位数字大于8时,如8.48,在计算过程中可按4位算 常见仪器: (1)滴定管、移液管、容量瓶:4位有效数字 (2)分析天平(万分之一)取4位有效数字 (3)标准溶液的浓度,用4位有效数字表示 3.有效数字修约规则 “四舍六入五留双”和“一次性修约” 0.727646→0.7276 0.47366→0.473711.235→11.24 11.245→11.24 11.24501→11.25 将3.5481修约为2位有效数字,不能先修约为3.55,再修约为3.6,而应该 一次修约为3.5
注意:1)分数、比例系数、实验次数、常数(如:π)等不记位数 2)pH计算,[H+]=5.0210-3 pH=2.299 有效数字按小数点后的位数计算 如:pH=11.058 3)误差、偏差及相对偏差,一般只保留一位有效数字 4)改变单位,不改变有效数字的位数: 常见仪器: (1)滴定管、移液管、容量瓶:4位有效数字 (2)分析天平(万分之一)取4位有效数字 (3)标准溶液的浓度,用4位有效数字表示 3. 有效数字修约规则 “四舍六入五留双”和“一次性修约” 0.727646→0.7276 0.47366→0.4737 11.235→11.24 11.245→11.24 11.24501→11.25 将3.5481修约为2位有效数字,不能先修约为3.55,再修约为3.6,而应该 一次修约为3.5 5)第1位数字大于8时,如8.48,在计算过程中可按4位算 如: 24.01mL 24.01×10-3 L
2.2有效数字的运算规则 1.加减运算:应以小数点后位数最少的的数字为依据,即结果的 位数取决于绝对误差最大的数据的位数 例: 0.0121 绝对误差:0.0001 25.64 0.01 +0.057 0.001 25.7091≈25.71 0.01 如 2.15+2.155+2.145+2.1451+2.1346 绝对误差:0.010.0010.0010.00010.00001 2.15+2.16+2.14+2.15+2.13=10.73 再如: 28.1 29.15 18.3659 +)15.46 -)10.15 -5.12 +)1.04643 +)12.375 =44.6 =19.00 =25.63
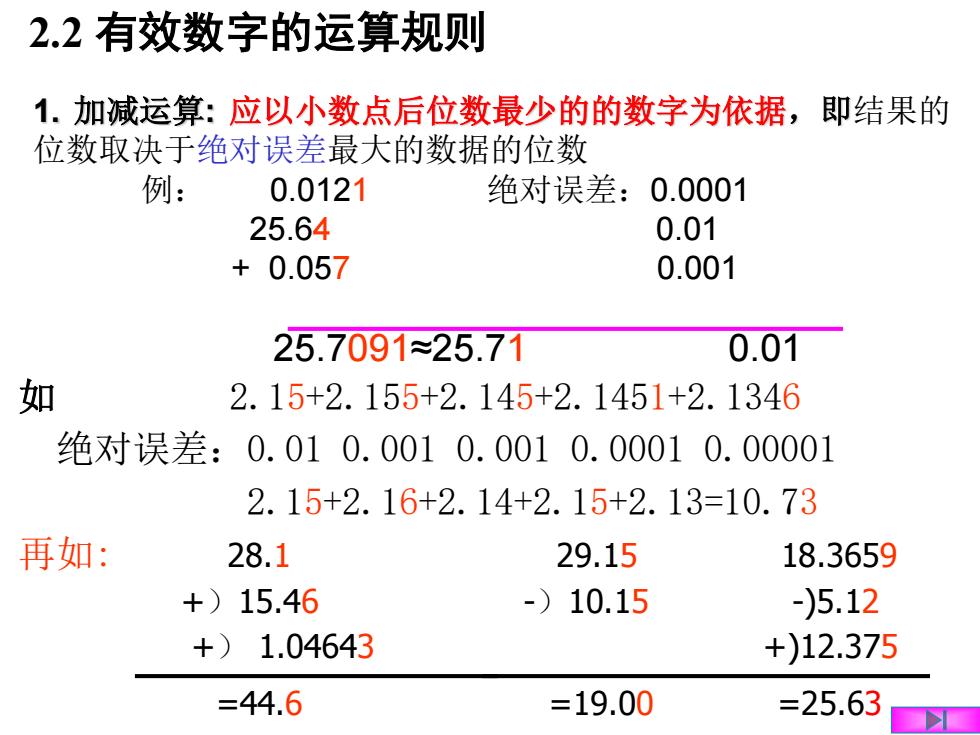
1. 加减运算: 应以小数点后位数最少的的数字为依据,即结果的 位数取决于绝对误差最大的数据的位数 例: 0.0121 绝对误差:0.0001 25.64 0.01 + 0.057 0.001 2.2 有效数字的运算规则 =44.6 如 2.15+2.155+2.145+2.1451+2.1346 绝对误差:0.01 0.001 0.001 0.0001 0.00001 2.15+2.16+2.14+2.15+2.13=10.73 再如: 28.1 29.15 18.3659 +)15.46 -)10.15 -)5.12 +) 1.04643 +)12.375 25.7091≈25.71 0.01 =19.00 =25.63
2.乘除运算时 有效数字的位数取决于相对误差最大的数据的位数 例:(0.0325x5.103x60.0/139.8=0.071179184=0.0712 0.0325±0.0001/0.0325×100%=±0.3% ±0.1% 5.103 ±0.001/5.103×100%=±0.02% 60.06 ±0.01/60.06×100%=±0.02% 139.8 ±0.1/139.8×100%=±0.07% 结果的有效数字位数一般与有效数字位数最少的那个数字相同 0.0325 ±0.3% 12.12 ±0.08% ×5.103 ±0.02% ×)0.156 ±0.6% 975 7272 000 6060 325 +)1212 +)1625 =1.89072≈1.89 ±0.5% 0.16584750.166 ±0.6%
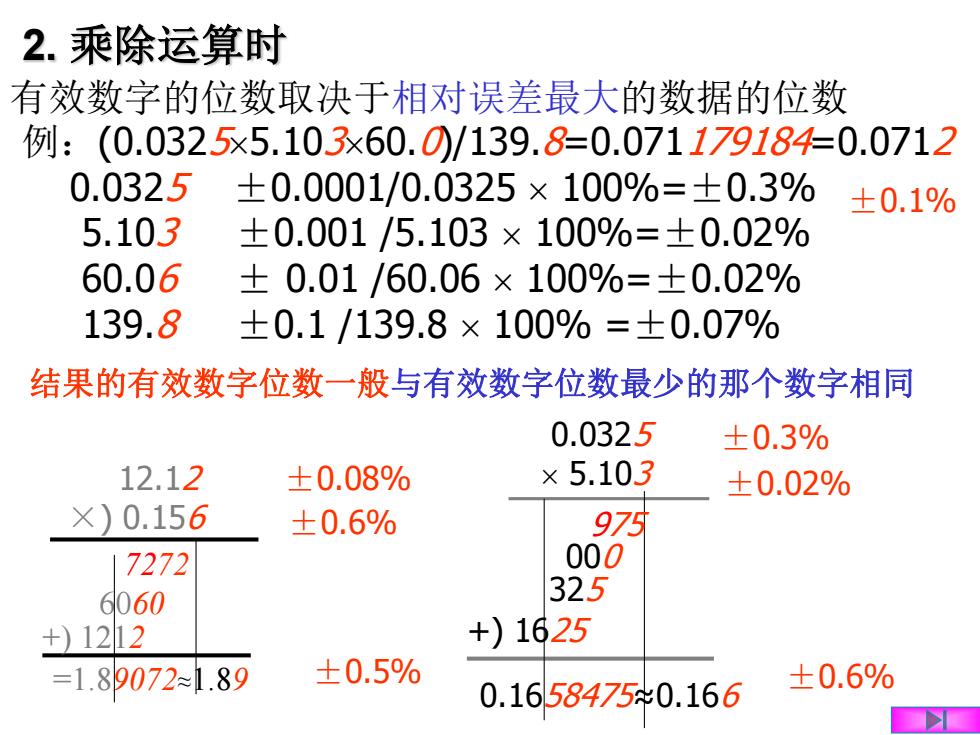
有效数字的位数取决于相对误差最大的数据的位数 例:(0.03255.10360.0)/139.8=0.071179184=0.0712 0.0325 ±0.0001/0.0325 100%=±0.3% 5.103 ±0.001 /5.103 100%=±0.02% 60.06 ± 0.01 /60.06 100%=±0.02% 139.8 ±0.1 /139.8 100% =±0.07% 2. 乘除运算时 0.0325 5.103 0.1658475≈0.166 ±0.1% ±0.6% ±0.3% 12.12 ±0.02% ×) 0.156 ±0.08% ±0.6% ±0.5% 结果的有效数字位数一般与有效数字位数最少的那个数字相同 7272 6060 +) 1212 =1.89072≈1.89 +) 1625 975 000 325