
《数学物理方法》教学大纲 课程性质专业必修课 课程编号 xx996107 课程名称 数学物理方法 适用专业物理学 先修课程高等数学、普通物理 总学时其中理论72学时,实验0学时 学分数45 一、课程简介 《数学物理方法》是物理学专业学生的基础课之一,是物理学工作者从事现代物理 研究不可缺少的基本知识。在高等数学和普通物理的基础上,以讲授古典数学物理方法 中的常用方法为主,适当介绍近年来的新发展。《数学物理方法》是前导课程《高等数 学》的延伸,为后继开设的《电动力学》、《量子力学》和《电子技术》等课程提供必需 的数学理论知识和计算工具。本课程在本科物理学专业中占有重要的地位。本专业学生 必须掌握它们的基本内容,否则对后继课的学习将会带来很大困难。 由于本大纲面向对象是二类本科院校物理专业学生,因此教学重心放在基本知识及 基本方法的讲授上,本课程较难的部分如特殊函数、格林函数法等不做要求,留给有兴 趣的学生自学。 二、课程教学目标 1、通过本课程的学习,使学生对《数学物理方法》的内容有一个总体了解。掌握 其中的基本概念,熟悉一些重要的理论及公式,并使所学到的知识在头脑中形成合理的 结构,为后一阶段理论物理课程的学习打下数学基础,也为今后工作中遇到的数学物理 问题的求解提供基础。 2、通过本课程的学习,使学生能运用学到的基本数学方法解决一类常见的物理问 题,能较顺利地学习本专业后继的物理课程。 3、学生通过本课程的学习,能熟悉在数学物理方法的创立过程中用过的创新思维 方法,如类比、推广、猜想及模型化等,为写出有特色的毕业论文创造条件。 三、课程教学基本要求 1、本课程的内容为数学课程,注重逻辑推理和具有一定的系统性和严谨性。但是, 它与其它的数学课有所不同。本课程内容有很深广的物理背景,实用性很强。因此,在 这门课的教学过程中,不能单纯地追求理论上的完美、严谨,而忽视其应用。学生在学
1 《数学物理方法》教学大纲 课程性质 专业必修课 课程编号 xx996107 课程名称 数学物理方法 适用专业 物理学 先修课程 高等数学、普通物理 总学时 其中理论 72 学时,实验 0 学时 学分数 4.5 一、课程简介 《数学物理方法》是物理学专业学生的基础课之一,是物理学工作者从事现代物理 研究不可缺少的基本知识。在高等数学和普通物理的基础上,以讲授古典数学物理方法 中的常用方法为主,适当介绍近年来的新发展。《数学物理方法》是前导课程《高等数 学》的延伸,为后继开设的《电动力学》、《量子力学》和《电子技术》等课程提供必需 的数学理论知识和计算工具。本课程在本科物理学专业中占有重要的地位。本专业学生 必须掌握它们的基本内容,否则对后继课的学习将会带来很大困难。 由于本大纲面向对象是二类本科院校物理专业学生,因此教学重心放在基本知识及 基本方法的讲授上,本课程较难的部分如特殊函数、格林函数法等不做要求,留给有兴 趣的学生自学。 二、课程教学目标 1、通过本课程的学习,使学生对《数学物理方法》的内容有一个总体了解。掌握 其中的基本概念,熟悉一些重要的理论及公式,并使所学到的知识在头脑中形成合理的 结构,为后一阶段理论物理课程的学习打下数学基础,也为今后工作中遇到的数学物理 问题的求解提供基础。 2、通过本课程的学习,使学生能运用学到的基本数学方法解决一类常见的物理问 题,能较顺利地学习本专业后继的物理课程。 3、学生通过本课程的学习,能熟悉在数学物理方法的创立过程中用过的创新思维 方法,如类比、推广、猜想及模型化等,为写出有特色的毕业论文创造条件。 三、课程教学基本要求 1、本课程的内容为数学课程,注重逻辑推理和具有一定的系统性和严谨性。但是, 它与其它的数学课有所不同。本课程内容有很深广的物理背景,实用性很强。因此,在 这门课的教学过程中,不能单纯地追求理论上的完美、严谨,而忽视其应用。学生在学
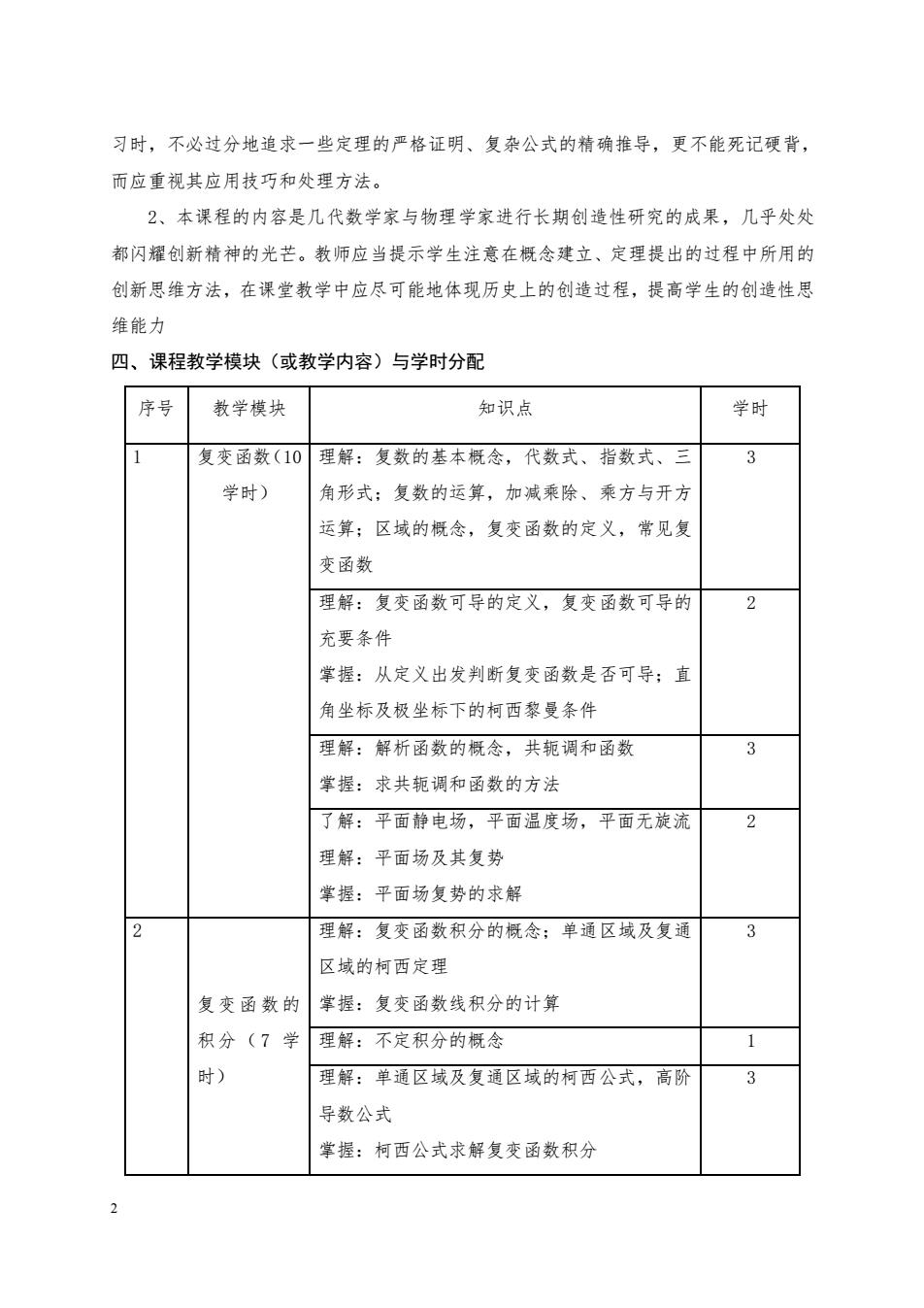
习时,不必过分地追求一些定理的严格证明、复杂公式的精确推导,更不能死记硬背, 而应重视其应用技巧和处理方法。 2、本课程的内容是几代数学家与物理学家进行长期创造性研究的成果,几乎处处 都闪耀创新精神的光芒。教师应当提示学生注意在概念建立、定理提出的过程中所用的 创新思维方法,在课堂教学中应尽可能地体现历史上的创造过程,提高学生的创造性思 维能力 四、课程教学模块(或教学内容)与学时分配 序号 教学模块 知识点 学时 复变函数(10理解:复数的基本概念,代数式、指数式、目 3 学时) 角形式:复数的运算,加减桑除、乘方与开方 运算;区域的概念,复变函数的定义,常见复 变函数 理解:复变函数可导的定义,复变函数可导的 2 充要条件 掌握:从定义出发判断复变函数是否可导:直 角坐标及极坐标下的柯西黎曼条件 理解:解析函数的概念,共轭调和函数 3 掌握:求共轭调和函数的方法 了解:平面静电场,平面温度场,平面无旋流 2 理解:平面场及其复势 掌握:平面场复势的求解 理解:复变函数积分的概念:单通区域及复通 3 区域的柯西定理 复变函数的 掌握:复变函数线积分的计算 积分(7学 理解:不定积分的概念 1 时) 理解:单通区城及复通区域的柯西公式,高阶 3 导数公式 掌握:柯西公式求解复变函数积分
2 习时,不必过分地追求一些定理的严格证明、复杂公式的精确推导,更不能死记硬背, 而应重视其应用技巧和处理方法。 2、本课程的内容是几代数学家与物理学家进行长期创造性研究的成果,几乎处处 都闪耀创新精神的光芒。教师应当提示学生注意在概念建立、定理提出的过程中所用的 创新思维方法,在课堂教学中应尽可能地体现历史上的创造过程,提高学生的创造性思 维能力 四、课程教学模块(或教学内容)与学时分配 序号 教学模块 知识点 学时 1 复变函数(10 学时) 理解:复数的基本概念,代数式、指数式、三 角形式;复数的运算,加减乘除、乘方与开方 运算;区域的概念,复变函数的定义,常见复 变函数 3 理解:复变函数可导的定义,复变函数可导的 充要条件 掌握:从定义出发判断复变函数是否可导;直 角坐标及极坐标下的柯西黎曼条件 2 理解:解析函数的概念,共轭调和函数 掌握:求共轭调和函数的方法 3 了解:平面静电场,平面温度场,平面无旋流 理解:平面场及其复势 掌握:平面场复势的求解 2 2 复变函 数的 积分( 7 学 时) 理解:复变函数积分的概念;单通区域及复通 区域的柯西定理 掌握:复变函数线积分的计算 3 理解:不定积分的概念 1 理解:单通区域及复通区域的柯西公式,高阶 导数公式 掌握:柯西公式求解复变函数积分 3
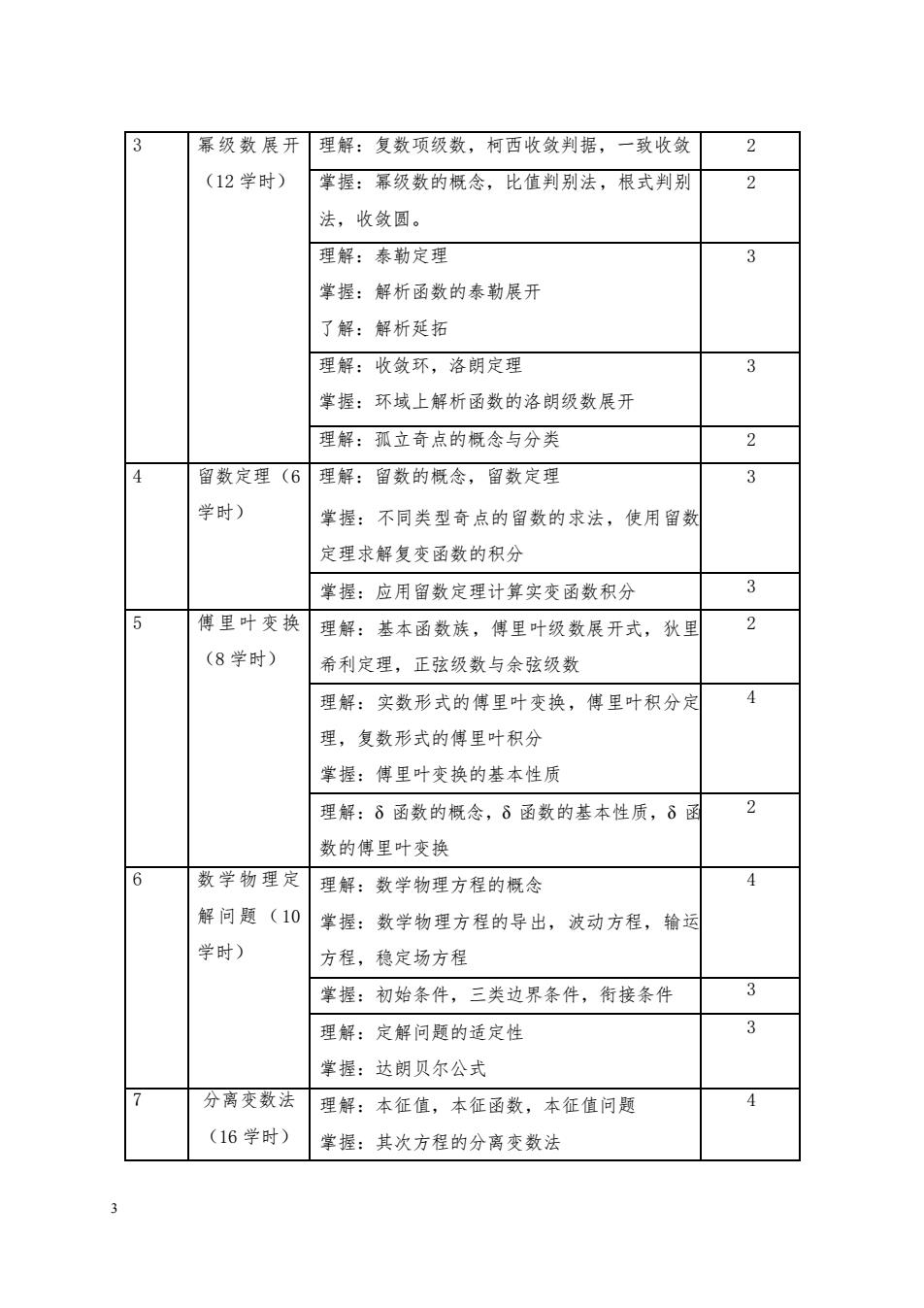
幂级数展开理解:复数项级数,柯西收敛判据,一致收敛 2 (12学时) 掌握:幂级数的概念,比值判别法,根式判别 法,收敛圆。 理解:泰勒定理 3 掌握:解析函数的泰勒展开 了解:解析延拓 理解:收敛环,洛朗定理 3 掌握:环域上解析函数的洛朗级数展开 理解:孤立奇点的概念与分类 2 留数定理(6理解:留数的概念,留数定理 3 学时) 掌握:不同类型奇点的留数的求法,使用留卖 定理求解复变函数的积分 掌握:应用留数定理计算实变函数积分 3 6 傅里叶变换 理解:基本函数族,傅里叶级数展开式,狄里 2 (8学时) 希利定理,正弦级数与余弦级数 理解:实数形式的傅里叶变换,傅里叶积分定 4 理,复数形式的傅里叶积分 掌握:傅里叶变换的基本性质 理解:6函数的概念,δ函数的基本性质,δ函 2 数的傅里叶变换 6 数学物理定理解:数学物理方程的概念 4 解间题(10 掌握:数学物理方程的导出,波动方程,输运 学时) 方程,稳定场方程 掌握:初始条件,三类边界条件,衔接条件 3 理解:定解问题的适定性 3 掌握:达朗贝尔公式 分离变数法理解:本征值,本征函数,本征值问题 4 (16学时) 掌握:其次方程的分离变数法
3 3 幂级数 展开 (12 学时) 理解:复数项级数,柯西收敛判据,一致收敛 2 掌握:幂级数的概念,比值判别法,根式判别 法,收敛圆。 2 理解:泰勒定理 掌握:解析函数的泰勒展开 了解:解析延拓 3 理解:收敛环,洛朗定理 掌握:环域上解析函数的洛朗级数展开 3 理解:孤立奇点的概念与分类 2 4 留数定理(6 学时) 理解:留数的概念,留数定理 掌握:不同类型奇点的留数的求法,使用留数 定理求解复变函数的积分 3 掌握:应用留数定理计算实变函数积分 3 5 傅里叶 变换 (8 学时) 理解:基本函数族,傅里叶级数展开式,狄里 希利定理,正弦级数与余弦级数 2 理解:实数形式的傅里叶变换,傅里叶积分定 理,复数形式的傅里叶积分 掌握:傅里叶变换的基本性质 4 理解:δ 函数的概念,δ 函数的基本性质,δ 函 数的傅里叶变换 2 6 数学物 理定 解问题 (10 学时) 理解:数学物理方程的概念 掌握:数学物理方程的导出,波动方程,输运 方程,稳定场方程 4 掌握:初始条件,三类边界条件,衔接条件 3 理解:定解问题的适定性 掌握:达朗贝尔公式 3 7 分离变数法 (16 学时) 理解:本征值,本征函数,本征值问题 掌握:其次方程的分离变数法 4
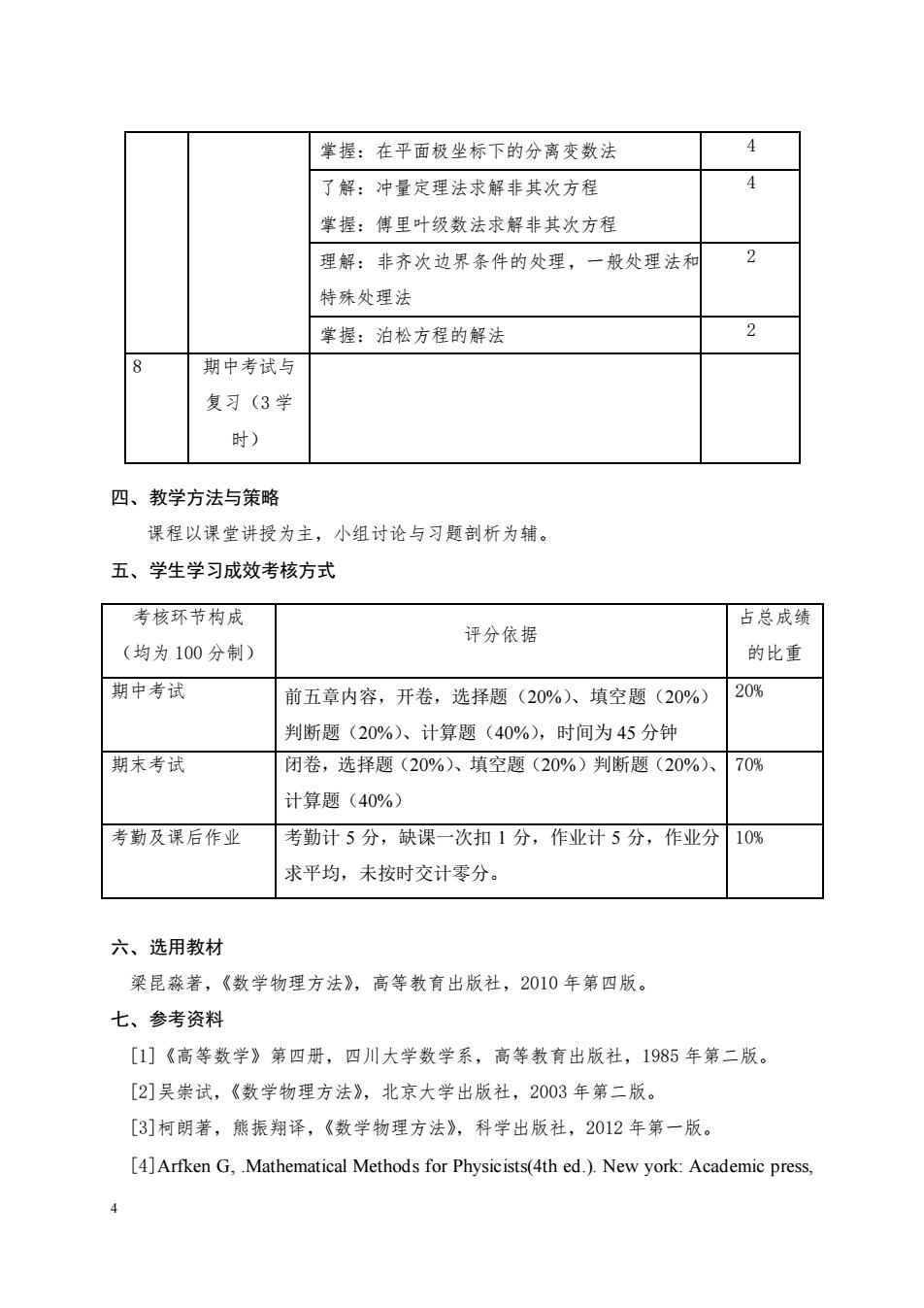
掌握:在平面极坐标下的分离变数法 了解:冲量定理法求解非其次方程 掌握:傅里叶级数法求解非其次方程 理解:非齐次边界条件的处理,一般处理法和 2 特殊处理法 掌握:泊松方程的解法 2 期中考试与 复习(3学 时) 四、教学方法与策略 课程以课堂讲授为主,小组讨论与习题剖析为辅。 五、学生学习成效考核方式 考核环节构成 占总成绩 评分依据 (均为100分制) 的比重 期中考试 前五章内容,开卷,选择题(20%)、填空题(20%) 20% 判断题(20%)、计算题(40%),时间为45分钟 期末考试 闭卷,选择题(20%)、填空题(20%)判断题(20%)、70% 计算题(40%) 考勤及课后作业 考勤计5分,缺课一次扣1分,作业计5分,作业分10% 求平均,未按时交计零分。 六、选用教材 梁昆淼著,《数学物理方法》,高等教育出版社,2010年第四版。 七、参考资料 [1]《高等数学》第四册,四川大学数学系,高等教有出版社,1985年第二版。 [2]吴崇试,《数学物理方法》,北京大学出版社,2003年第二版。 [3)]柯朗著,熊振翔译,《数学物理方法》,科学出版社,2012年第一版。 [4]Arfken G,Mathematical Methods for Physicists(4th ed.).New york:Academic press
4 掌握:在平面极坐标下的分离变数法 4 了解:冲量定理法求解非其次方程 掌握:傅里叶级数法求解非其次方程 4 理解:非齐次边界条件的处理,一般处理法和 特殊处理法 2 掌握:泊松方程的解法 2 8 期中考试与 复习(3 学 时) 四、教学方法与策略 课程以课堂讲授为主,小组讨论与习题剖析为辅。 五、学生学习成效考核方式 六、选用教材 梁昆淼著,《数学物理方法》,高等教育出版社,2010 年第四版。 七、参考资料 [1]《高等数学》第四册,四川大学数学系,高等教育出版社,1985 年第二版。 [2]吴崇试,《数学物理方法》,北京大学出版社,2003 年第二版。 [3]柯朗著,熊振翔译,《数学物理方法》,科学出版社,2012 年第一版。 [4]Arfken G, .Mathematical Methods for Physicists(4th ed.). New york: Academic press, 考核环节构成 (均为 100 分制) 评分依据 占总成绩 的比重 期中考试 前五章内容,开卷,选择题(20%)、填空题(20%) 判断题(20%)、计算题(40%),时间为 45 分钟 20% 期末考试 闭卷,选择题(20%)、填空题(20%)判断题(20%)、 计算题(40%) 70% 考勤及课后作业 考勤计 5 分,缺课一次扣 1 分,作业计 5 分,作业分 求平均,未按时交计零分。 10%

1997。 [5]周治宁,吴崇试,钟毓澍著,《数学物理方法习题指导》,北京大学出版社,2004年 第一版。 大纲起草人: 何杰辉 大纲审核人:丁持坤 大纲批准人: 谢四莲 日期:2016年12月20日 5
5 1997。 [5]周治宁,吴崇试,钟毓澍著,《数学物理方法习题指导》,北京大学出版社,2004 年 第一版。 大纲起草人: 何杰辉 大纲审核人: 丁持坤 大纲批准人: 谢四莲 日期:2016 年 12 月 20 日