
目录 第一章光的电磁理 1-1麦克斯韦方 1-2电磁场的波动 1-3平面磁 1-4球面波和柱面波的波公 1-5光波的辐射,射 §1-6电磁场的边界条6 1-7光在二透明电介质分界面上的反射和 1-8全4 1-9光在金属表面上的 第二章光波的迭加与分析0 §2-1两个频率相同、振动方向相同的单色光波的0 2-2 2-3两个频率相同、振动方向互相垂直的光波的6 2-4不同频率的两个单色光波的 2-5光波的分 第三章光的干涉和干7 3-1产生干涉的7 3-2杨氏干实 $3-3 .阵... 3-4条纹的见 3-5平行平板产生的干 3-6楔形平板产生的干 3-7用牛顿环测量透镜的曲*0 3-8平面干 3-9迈克耳逊干 3-10.. 3-11马赫-泽德干 3-12平行平板产生的多光束干 3-13法布里-珀罗干涉仪和陆-盖尔 §3-14 多光束干涉原理在薄膜理论中的应用 第四章 光的衍射 4-1惠更斯-菲涅耳原 4-2基尔霍夫射公 4-3菲涅耳衍射与夫琅和费 4-4菲涅耳带6 4-5菲涅耳圆孔 4-6菲涅耳圆衍射 4-7波带2

4-8菲涅耳直边 4-9夫琅和费矩孔和单7 §4-10夫琅和费圆孔2 4-11光源大小对衍射条纹的影 4-12光学系统的分本6 4-13双缝射瑞利干 4-14衍射光 4-15平面定向光栅和光栅光0 4-16面光 4-17计量光栅(莫尔光 第五章 傅里叶光学 §5-1 空间频率及其物理意义 §5-2 单色光波复振幅的分解 5-3衍射理论中的傅里叶分析法 5-4透镜的傅里叶变换性7 5-5阿贝成象理论及阿贝-波尔 5-6相干光学处理系统-双透镜相干成系3 5-7简单空间滤波器的应用 5-8位相滤波器,暗场法和泽尼克 5-8 5-9切趾术(变 5-10相干光成象系统的频谱分析,相干传递 5-11 11非相干成象系统的率响应,光学传递6 §5-12 全息照相的一般理5 5-13 利思-乌帕特尼克斯离轴全 第六章 光的偏振与晶体光学基础 .......199 §6-1 偏振光和自然 6-2 双折 $6-3 偏振棱镜和片0 6-4 偏振的矩阵表示 示 §6-5 偏振光的干涉 6-6 旋光现象 §G-7 磁光效应 6-8 电光效应 6-9光测弹性方法和玻璃内应力的 第七章 光的量子性8 §7-1 辐射能的子化 7-2光的发射与吸收的子模 7-3光的自发发射、受激发射与受吸 7-4光谱线的 第八章激光 8-1光在介质中的大9 8-2激光

8-3振腔的几何光学理6 8-4光学谐振腔的物理光学理 8-5激光的谱线7 8-6激光器的类 8-7激光器的7 8-8调Q 8-9锁模技术 8-10非线性7 8-11环形激光器(激光 8-12光通0 8-13薄膜波导与集 附3 I高斯定理、斯托克斯定理及矢量分析的几个基本公 傅里叶级数和傅里8 【二维的傅里叶 V亥姆霍兹-基尔霍夫积分定理,基尔霍夫衍射公式 V贝塞尔38 0 矩阵的基本性 基本物理 部分习题答案

第一章光的电磁理论 十九世纪六十年代,麦克斯韦(Max©1)总结了前人在电磁学方面的研究成果,建立了 经典电磁理论。与此同时,他把光学现象和电磁现象联系起来,指出兆也是一种电磁被,从 而产生了光的电磁理论。光的电磁理论的确立,推动了光学及整个物理学的发展。现代光学 尽管产生了许多新的领域,并且许多光学现象需要用量子理论来解释,但是光的电磁理论仍 然是掌握现代光学的一个重要的基础。本章将简要叙述光的电磁理论以及它对一些光学现象 如光的反射和折射现象所作的简单处理,使我们对光的电磁本性有一个概念性的认识。关于 光的电磁理论的系统论述可以参考其它一些书籍日。 §1-1麦克斯韦方程组 电磁场的普遍理论总结为麦克斯韦方程组,它是麦克斯韦把稳定电磁场(静电场和稳恒 电流的磁场)的基本规律推广到不稳定电磁场的普遍情况而得到的。从方程组出发,结合具 体的条件,可以定量地计算在这些给定条件下发生的光学现象,例如光的辐射和传播、光的 反射、折射、干涉、衍射和光与物质相互作用等现象。 静电场和稳恒电流的磁场的基本规律可以总结为下面四个方程式 D.do=Q (1-10 E.d=0 (1-2) B.do=0 (1-3) H.d=I 1-4) 式中D、E、B、H分别表示电感强度(电位移失量)、电场强度、磁感强度和磁场强度,对 d和l的积分分别表示对任一闭合曲面和闭合回路的积分,Q表示积分闭合曲面内包含的总 电量,I表示积分闭合回路包围的传导电流。式(1-1)是我们熟知的高斯(Gau55)定理的数学 求示,式(1-4)是安培(Ampere)环路形律 这些方程式只在稳定情况下适用,要应用到 不稳定情形,必须将它们作适当的修改和推广。麦 s 克斯韦完成了这一工作,他假定在不稳定情况下 式(1-1)和(1-3)仍然成立,式(1-2)应代以法拉第 (Faraday)电磁感应定律,只是式(1-4)需要修改 图1-】永磁铁向闭合线圈移 根据法拉第电磁感应定律,一闭合线圈处在 动时产生感应电动势 变化的磁杨中(图1-1)©,会产生感应电动势,这感应电动势的大小与磁通量的时间变化率成 比例,它的方向由左手定则决定,以式子表示
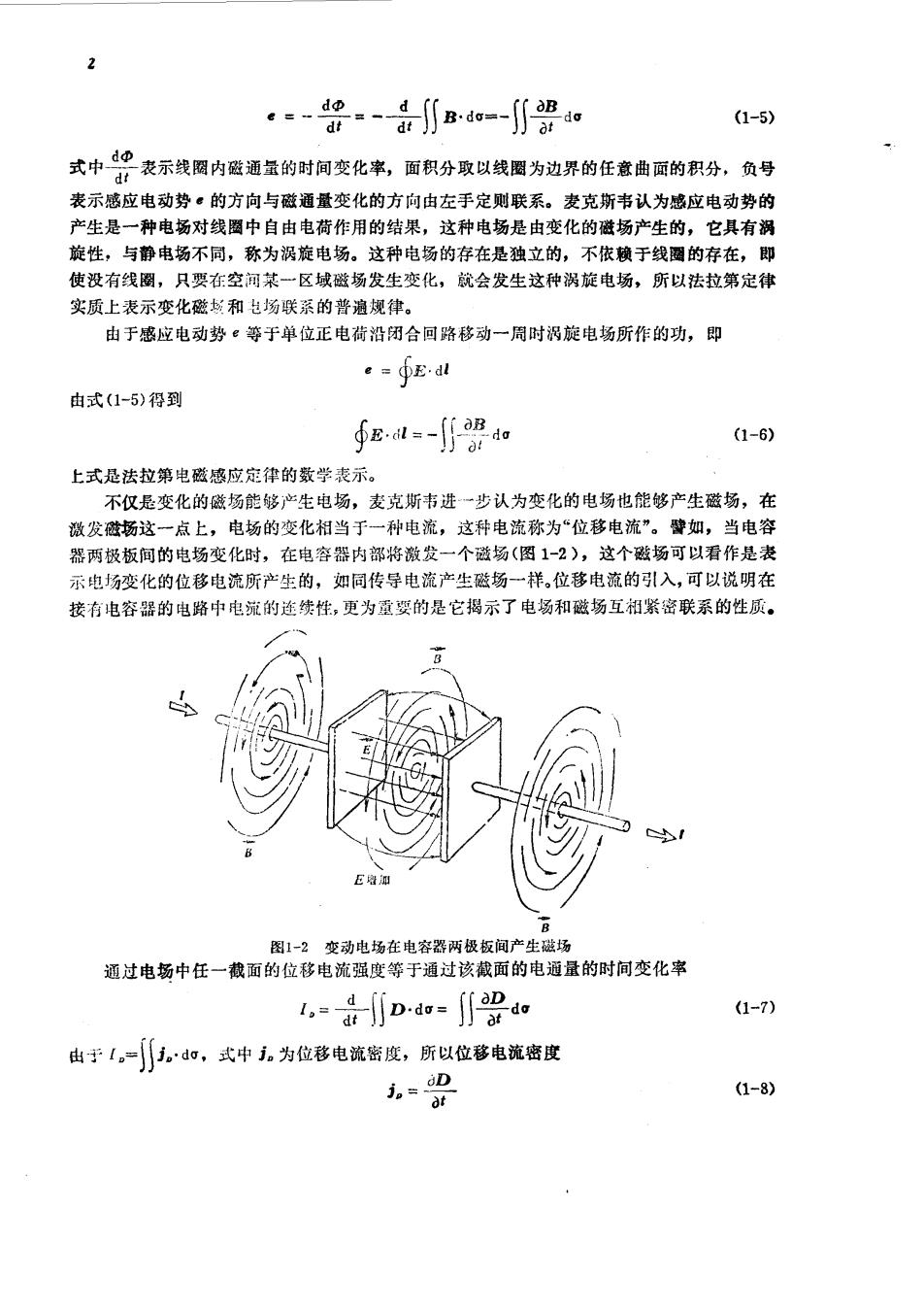
2 。=-0s-Bdo=-∬o (1-5) 式中。表示战圈内医通蛋的时间空化常,面积分攻以线圈为边界的任章鱼面的积分,负号 表示感应电动势。的方向与磁通量变化的方向由左手定则联系。麦克斯韦认为感应电动势的 产生是一种电场对线圈中自由电荷作用的结果,这种电场是由变化的磁场产生的,它具有湖 旋性,与静电畅不同,称为祸旋电场。这种电场的存在是独立的,不依赖于线圈的存在,即 使没有线圈,只要在空河某一区域磁场发生变化,就会发生这种涡旋电场,所以法拉第定律 实质上表示变化磁和电场联系的普遍规律。 由于感应电动势。等于单位正电荷沿闭合回路移动一周时涡旋电场所作的功,即 。=∮Edl 由式(1-5)得到 ∮s1-明设加 (1-6) 上式是法拉第电磁感应定律的数学表示。 不仅是变化的隧场能够产生电场,麦克斯韦进一步认为变化的电场也能够产生磁场,在 激发磁畅这一点上,电场的变化相当于一种电流,这种电流称为“位移电流”。如,当电容 器两极板间的电场变化时,在电容器内部将激发一个磁场(图1-2),这个磁场可以看作是表 示电场变化的位移电流所产生的,如同传导电流产生磁场一样,位移电流的引入,可以说明在 接有电容器的电路中电荒的连续性,更为重要的是它揭示了电场和磁场互祁紫密联系的性质。 图1一2恋动电场在申究寒两极板间产生磁场 通过电场中任一截面的位移电流强度等于通过该截面的电通量的时间变化率 ,jD:o=∬设o (1-7) 出于I。=。do,式中j。为位移电流密度,所以位移电流密度 =0 (1-8)

3 位移电流和传导电流是两个不同的物理餐念,传导电流意味著电荷的流动,而位移电流 却意味着电场的变化,但是两者在产生磁杨方面是等效的。因此,在不稳定电磁场的情况下, 磁场既包括传导电流产生的磁杨,也包括位移电流产生的磁扬。这样式(1-4)变为 ∮Hal=1+j∬识o (1-9) 总结起来,不稳定电磁场的普遍规律由下列四个方程表示 D.do=Q B.do=0 fe=-∬如 (1-10) ∮Ha1+j0o 这四个方程通常称为积分形式的麦克斯韦方程组。 在实际应用中,由于积分形式的麦克斯韦方程组不适用于求解电磁场中某一给定点的场 量这类问题,所以通常使用的是方程组的微分形式。要求得方程组的微分形式,可根据积分 学中的定理把各有关积分式变换为相应的微分方程式。 对于方程组的第一式,如果闭合曲面积分蚊内包含的电荷是连续分布的,则Q=川, 式中?为电荷密度,积分域是闭合曲面包的体积。这样 D.do =edr 根据积分学中的高斯定理(见附录I) D.do=v.Dav 因此 VD=P (1-11) 式中算符=及+》+,,称为哈密颜amilto)算符,、、名分别为, 、:隆标销的单位矢,VD0++识表示D的散度《他记为出D).D D,、D,分别为D在×、y,2座标轴上的分量。式(1-11)就是方程组第一式的微分形式。 再如方程组第四式,如把I写为I=月j,式中j为传导电流密度,表示垂直通过单 位面积的电点量,这样方程变为 ∮al=jjo+∬Co 根据积分学中的斯托克斯(Stokes)定理(见附录I) ∮Hdl=Jjv×Hdo 得到 VxH-D (1-12)

4 式中×H表示H的旋度(也记为rotH或curlH),同样地,容易得到第二方程和第三方程的 微分形式: V.B=0 (1-13) 和 (1-14) 因此,微分形式的麦克斯韦方程组为: V.D-P V.B=0 V×E=-识 (1-15) VxH- 式(1-15)结合下列所调物质方程 D=tE,.B=WH,j=YE 构成一组完整的反映电磁场普道规律的方程组。式中。、“、Y分别称为介电系数(或电容 率),磁导率和电导率。在各向同性的均匀电介质中,Y=0,。和“为常数,在真空中。 =,=8.8542×1012库心2/牛米,4=4,=4×10-牛./佛仑。 §1-2电磁场的波动性 从上节的讨论,可得到两个结论:第一,任何随时间变化的磁场在周围空间产生电场, 这种电场具省满旋性,电场的方向由左手定则决定(图1-1),第二,任何随时间变化的电场 (位移电流)在周围空间产生磁场,磁场是涡旋的,磁场的方向由右手定则决定(图1-2)。出 此可见,电场和磁场紧密相联,其中一个起变化时,随即出现另一个,它们互相激发形成统 一的场 电磁场。变化的电磁场可以以一定的速度向周围空间传播出去。设在空间某区域 内电场有变化,那么在邻近的区域就要引起随时间变化的磁场,这变化的磁场又在较远的区 域引起新的变化电场,接着这新的变化电场又在更远的区域引起新的变化磁场,变化的电场 和磁场的交替产生,使电磁场传播到很远的区域。电磁场在空间以一定速度由近及远的传播 过程,称为电磁波。 从麦克斯韦方程组出发,可以证明电磁场的传播具有波动性。为简单起见,我们讨论在 无限大均匀介质中的情况,这时。=常数,“=常数,并且在远离辐射源的区域,不存在自 由电荷和传导电流(p=0,j=0),因而麦克斯韦方程组简化为 7.E=0 v.H=0 xE-识 (1-16) xH=:沿

5 取第三式的旋度,并将第四式代入,得到 7x(x团=-xH=…5 根据矢量分析公式〔见附录式(I-16) 7×(7XE)=7(V.E)-VE 由于7·E=0,所以 V×(×E)=-vE 因此 V'B-CH-2E-0 对于H,同样可以得到 -的-0 示 (1-17) 以上两式化为 -E=0 (1-18) H-H=0 (1-19) 式(1-18)和(1-19》是熟知的波动微分方程,表明电场和磁场以波动形式在空间传播,传播 速度为(=√示小。麦克斯韦理论的这一结论已为后人的实践所证实。189年,赫兹(Hrt) 在实验中得到了波长为60厘米的电磁波,观察了电磁被在金属镜面上的反射,在石蜡制成的 棱镜中的折射,以及干涉现象。赫兹的实验不仅以无可登疑的事实证实了电磁波的存在,而 且也证明了电磁波具有光波的性质。 电磁波在介质中的传播速度由式(1-17)给出,根据式(1-17),电磁波在真空中的传据 速度 1 cEM (1-20) 式中,和,为真空中的介电系数和磁导率,已知,=8.8542×10-库仑/华领·*2,4,=4m× 107件顿.2/库仑,所以 e-√8.854210×4x×107=2.99794x10*/t 这个数值与实验中测定的真空中光速的数值非常接近(现在测定的真空中光速的最精确的数 值为c=2.997924562×10米/秒士1.1米/粉)。在历史上,岁克斯韦曾以此作为重要依据捉出 光的电磁理论并预言光是一种电磁波(当时麦克斯韦利用韦伯(Weber)和科尔劳许(Kohlr- u5ch)的实验结果计算出电磁波在真空中的速度为3,1074×10米/,而1848年斐索(Fizcau) 测量出的光速为3.14858×10米/)

6 现在已经知道,除了光波和无线电波外,x射线、Y射线也都是电磁波,它们的波长 比光波波长更短,但它们在木质上与光波或无线电波完全相同。我们按照波长或颜率把这些 电磁波排列成谱,称为电磁波谱,如图1-3所示。通常所说的光学区或光学频谱,包括紫外 线,可见光和红外线,被长范围约从10埃(1埃=10米)到1毫米。可见光是人限眼可以感觉 到各种颤色的光波,被长范围从0.40微米到0.76微米(4000埃到7600埃)。紫外线和红外 线则不能引起规说。 无线电波 红外级可见光紧外线工射线 ·产射线 02 09 0-2 0 3xi0° 310:31093x4u3x043x1063x0“ 3x0 图1-3电磁波谱 由式(117)和(1-20),可以得到电磁波在传播介质中的绝对折射溶 (1-21) 式'和'分州称为相对介电系数和相对磁导率。除了铁磁物质之外,对于大多数物质,只 有很网的磁性,心1,因而上式变为 n=/7 (1-22) 这个火系称为麦克斯书关系。表1-1列出了一些物质的√的数值和对于光波(钠光D线入= 5893埃)的折射常n(√的数值是对于60赫的低频电场测出的)。可见,对于化学结构 简单的气体,两者符合得很好。对于液体烃,例如对苯也有很好的近似,但对于许多固体 (如骏墙)和一些液体,两者相差较大。这是因为‘的数值与频率有关,对于光波,频率极高 (10*赫),所以对光波测出的折射率与低频下测出的√了的数值自然相差较大。介电常数 '或台折射率:随频率变化的关系,只有把物质的原子结构考虑进去才能处理。 麦1-1麦克斯韦关系 在0℃】大气压下的气体 20℃体 室祖下的图第 物度 物度 i.000294 1.000293 1.51 1.501 金刚石 4.06 2.A9 1.00003 ,000036 8.96 1.333 1.6 1.55 5.0 136 溶政 氧化要 19 1.458 1.00045 四氧化 4.63 1461 氧化 1.50 §1-3平面电磁波 波动微分方程(1-18)和(1-19)是两个偏微分方程,它们的解可以有多种形式,平面被、 球面波和柱面波都可满足方程。在求解方程时,要根据E和H满足的边界条件和初始条件, 决定解的具体形式。这里,以平面波为例,求解微分方程,并讨论平面波在各向同性均匀遗

明介质中传播的一些特性。 一、波动分方程的解 假设平面波沿直角座标系xy2的x方向传播(图1-4),那么电磁场值与y、z座标无 关,电磁场值只是¥和:的函数。这样,电磁场的波动方程(1-18)和(1-19》化为 (1-23) (124) 飞=4-总11+日 因而 是(警+能船)品(+} ·是(设+)器+品(+)品 +2+器 叫样 8三(-28品+5】 所以 85-5=-的0 0 对积分得到 B=8(6) 居()为飞的任意函数。再对:积分得到 E=g()d+f(n)=f() +f(n)=f,- )+(:+) 千和f:为两个任意函数。f,表示以速度” 沿 x正方向传插的波,f:表示以同一速度沿 x负方向前进的波。因为我们讨论的是由循 射源(光源)向外辐射的波的传插问题,所以 只取第一项, =1(:-))-2) 按同样的方法解方程(1-24),也会得到 图1-4沿x方向传湖的平面电磁破