中国科学技术大学：《科学与社会》课程教学资源（研讨讲稿）狄拉克是如何预言反物质的

狄拉克是如何预言反物质的？ 叶邦角 中国辩学我术大 ,物理学院 University of Science and Technology of China Schrodinger 能量与动量的经典关系 E= 2m 量子力学对应算符 B-品 and 币一-0 Schr6 dinger方程： ERWIN -p .0 SCHRODINGER 2m 1887 967 波函数的解为： b=Ne(应-E ih=H 1

1 叶邦角 方程: 能量与动量的经典关系 量子力学对应算符 波函数的解为：

Klein-Gordon 相对论E和p关系 E2=+m2 量子力学对应算符 and 币- Oskar Klein Klein-Gordon方程 (相对论Schrodinger方程) 那0=-26+m26 or (o+m)x)=0 or: (a,+m2)r)=0 方程的解 能量本征值： o(x)=Ne-ipuah E2=+m2 能量可以取+值： E=土v+m Walter Gordon Dirac Paul Dirac试图找到tried to find an equation that was relativistically correct, but linear in d/dt to avoid negative energies (and linear in d/dx (or V)for Lorentz covariance) He found an equation that turned out to describe spin-1/2 particles and predicted the existence of anti-particles 2

2 or : 能量本征值: 相对论E 和 p关系 量子力学对应算符 方程（相对论 方程） 方程的解 能量可以取+-值： Oskar Klein Walter Gordon Paul Dirac 试图找到tried to find an equation that was  relativistically correct,  but linear in d/dt to avoid negative energies  (and linear in d/dx (or ) for Lorentz covariance) He found an equation that  turned out to describe spin-1/2 particles and  predicted the existence of anti-particles

Dirac 相对论线性方程？？ 广义形式的哈密顿方程， Hw=(a.币+3m)边 平方后必须满足 0=(量+m) 需要找到两个系数α和邮 H2 (aipi+Bm)2v with:i=1,2,3 (onaj ajo)pipj+(o+Bon)pom+B2m2 =1 =0>j =0 =1 所以，a和B必须满足 ●a12=a22=a32=2 ,2,a3,B anti-commute with each other Dirac >什么是a和B? 最低维的矩阵是4x4!? 因此，Dirac表示为： a-(8） ； =(69） 0 1 01 0 0= ；-(09】 H一品，市--0 会0-(a+阿 8 + +i0测 +0ay02 w-m地=0 3

3 相对论线性方程 ?? 广义形式的哈密顿方程, 平方后必须满足 需要找到两个系数a和b 所以, αi 和 β 必须满足 α1 2 = α2 2 = α3 2 = β2 α1,α2,α3, β anti-commute with each other  什么是α 和 β ?? 最低维的矩阵是 4x4 !? 因此，Dirac 表示为:

Dirac (o,-m)=0 得到著名的Dirac方程： (i8.-m)中=0 with:"=(B,Ba)=Dirac y-matrices for each j=1.2.3.4 ()=0 PAM DIRACOM PHYSICIST 0U=m业 184 Dirac (o-m)=0 (9)2()2+()号+(8)是-(6)可 波函数yw的解？ 试探波函数 (y"pu-m)u(p)=0 ()=u(p)e-ipr or (p-m)u(p)=0 [(8)-(8)r-()()-0 两个联立方程 (行·uB=(E-m)uA (G·uA=(E+m)uB 4

4 得到著名的 Dirac 方程:  波函数ψ的解 ?? 试探波函数 两个联立方程

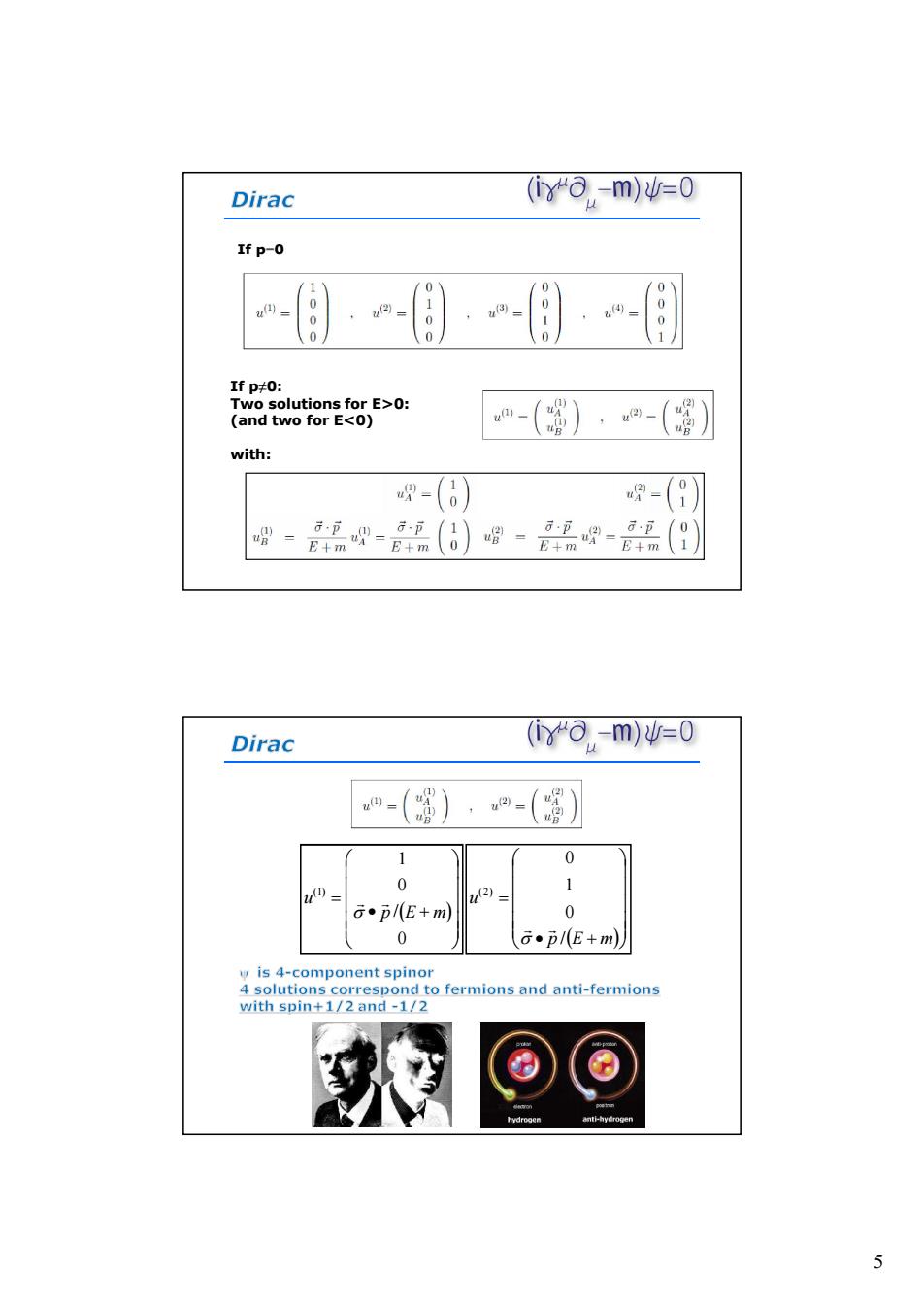
Dirac (a,-m)=0 If p=0 0 0 u@)- 0 ，u 0 0 1 0 0 1 If p#0: Two solutions for E>0: (and two for E<0) u) with: - 1 唱 :=B+m G.p 1 u唱= 豆=E+m 6…p 0 E十m 0 E+m Dirac (o-m)=0 -( 1 0 0 1 n四= u2)= G·p/(E+m) 0 0 G●p/(E+m yis 4-component spinor 4 solutions correspond to fermions and anti-fermions with spin+1/2 and-1/2 5

5 If p=0 If p≠0: Two solutions for E>0: (and two for E<0) with:                  0 / 0 1 )1( mEp u                   mEp u / 0 1 0 )2( 