
4.5金属的热电子发射和接触电势 一.功函数 二热电子发射 三.接触电势 参考:黄昆书6.2节p286-290 Kittel8版17.3.1;17.3.2节p336-337 在前面的讨论中,由于使用了周期性边界条件,我们所推 导的金属性质仅适合于无限大的金属,故没有关注金属表面势 场的影响,箱式模型假定电子气存在于不能穿透的壁的箱内, 即是说对电子而言,箱外的势能比箱内的势能无限地大,但实 验否定了这个假定,有限的能量足以使电子脱离金属,因此 为了从理论上讨论电子发射,修改箱式模型为一个具有一定 穿透性的箱壁是必要的
4.5 金属的热电子发射和接触电势 一. 功函数 二. 热电子发射 三. 接触电势 参考:黄昆书 6.2节 p286-290 Kittel 8版 17.3.1;17.3.2 节 p336-337 在前面的讨论中,由于使用了周期性边界条件,我们所推 导的金属性质仅适合于无限大的金属,故没有关注金属表面势 场的影响,箱式模型假定电子气存在于不能穿透的壁的箱内, 即是说对电子而言,箱外的势能比箱内的势能无限地大,但实 验否定了这个假定,有限的能量足以使电子脱离金属,因此 为了从理论上讨论电子发射,修改箱式模型为一个具有一定 穿透性的箱壁是必要的
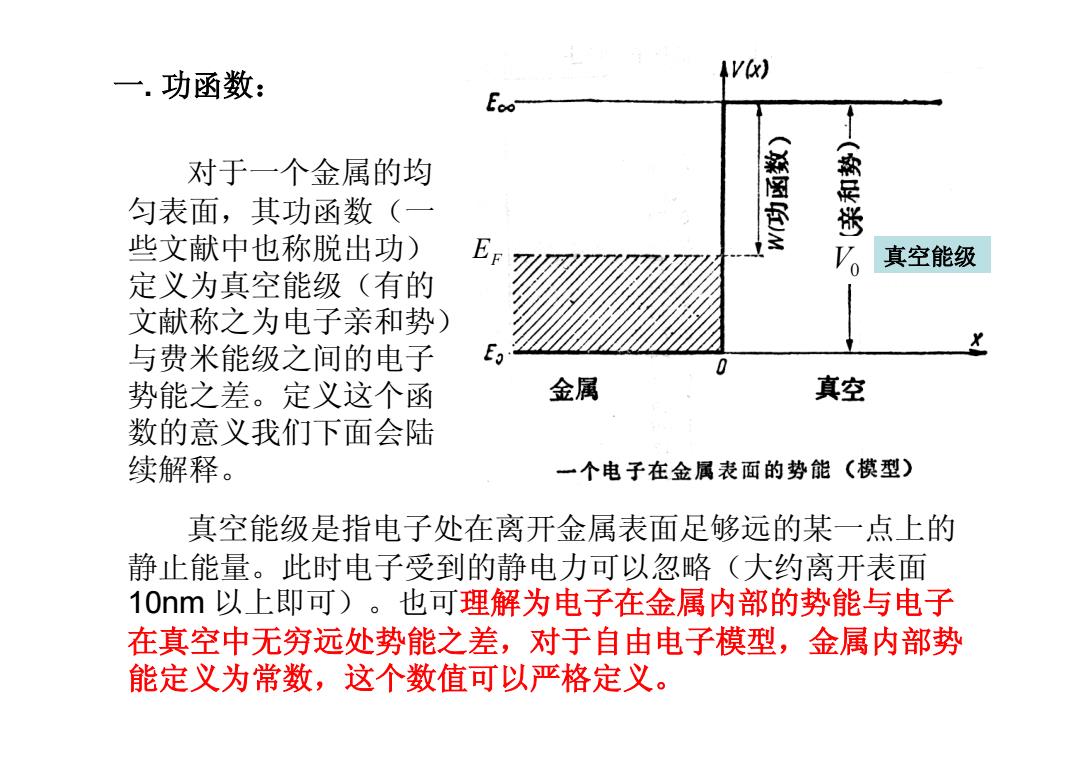
一.功函数: AV() 对于一个金属的均 (含4 匀表面,其功函数(一 # 些文献中也称脱出功) V。 真空能级 定义为真空能级(有的 文献称之为电子亲和势) 与费米能级之间的电子 势能之差。定义这个函 金属 真空 数的意义我们下面会陆 续解释。 一个电子在金属表面的势能(模型) 真空能级是指电子处在离开金属表面足够远的某一点上的 静止能量。此时电子受到的静电力可以忽略(大约离开表面 10nm以上即可)。也可理解为电子在金属内部的势能与电子 在真空中无穷远处势能之差,对于自由电子模型,金属内部势 能定义为常数,这个数值可以严格定义
一. 功函数: 对于一个金属的均 匀表面,其功函数(一 些文献中也称脱出功) 定义为真空能级(有的 文献称之为电子亲和势) 与费米能级之间的电子 势能之差。定义这个函 数的意义我们下面会陆 续解释。 真空能级是指电子处在离开金属表面足够远的某一点上的 静止能量。此时电子受到的静电力可以忽略(大约离开表面 10nm 以上即可)。也可理解为电子在金属内部的势能与电子 在真空中无穷远处势能之差,对于自由电子模型,金属内部势 能定义为常数,这个数值可以严格定义。 EF V0 真空能级

功函数的详细说明: 在金属内部,自由电子受到正离子的吸引,由于各金属离 子的吸引力相互抵消,电子所受的净合力为0。但金属表面的 电子由于有一部分离子的吸引力不能被抵消而受到净吸引力, 阻止其逸出金属表面。如同在金属表面形成一个势垒一样。因 此金属中的电子可以看成是处于深度为V,势阱中的电子系统。 实际上有可能被激发而逸出金属的电子只是在费米能附近, 因此,有 W='。-EE 其中V为真空能级,即电子跑到无穷远处所具有的势能, V也可看成是势阱的深度;功函数W~几个eV
功函数的详细说明: 在金属内部,自由电子受到正离子的吸引,由于各金属离 子的吸引力相互抵消,电子所受的净合力为 0 。但金属表面的 电子由于有一部分离子的吸引力不能被抵消而受到净吸引力, 阻止其逸出金属表面。如同在金属表面形成一个势垒一样。因 此金属中的电子可以看成是处于深度为 V0 势阱中的电子系统。 实际上有可能被激发而逸出金属的电子只是在费米能附近, 因此,有 W = - V E 0 F 其中V0为真空能级,即电子跑到无穷远处所具有的势能, V0也可看成是势阱的深度;功函数W~几个eV
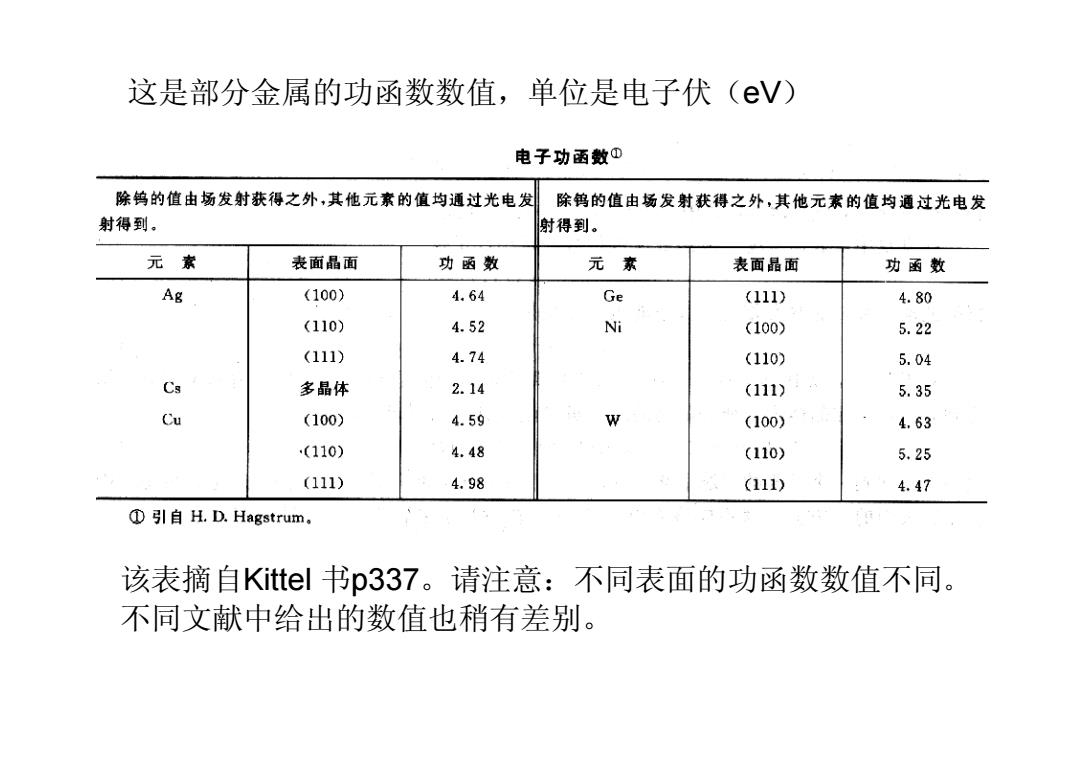
这是部分金属的功函数数值,单位是电子伏(eV) 电子功函数① 除钨的值由场发射获得之外,其他元素的值均通过光电发 除钨的值由场发射获得之外,其他元素的值均通过光电发 射得到。 射得到。 元素 表面晶面 功函数 元素 表面晶面 功函数 Ag (100) 4.64 Ge (111) 4.80 (110) 4.52 Ni (100) 5.22 (111) 4.74 (110) 5.04 Cs 多晶体 2.14 (111) 5.35 Cu (100) 4.59 W (100) 4,63 (110) 4.48 (110) 5.25 (111) 4.98 (111) 4.47 ①引自H.D.Hagstrum。 该表摘自Kittel书p337。请注意:不同表面的功函数数值不同。 不同文献中给出的数值也稍有差别
这是部分金属的功函数数值,单位是电子伏(eV) 该表摘自Kittel 书p337。请注意:不同表面的功函数数值不同。 不同文献中给出的数值也稍有差别

金属中的电子克服束缚跳出金属,根据其获得能量的方式 可以区分为: 1.高温导致的热电子发射; 2.强电场导致的场致发射; 3.光照导致的光致发射: 4.电子撞击产生的次级电子发射; 5.表面上的放热反应导致的外激发射,或更一般地说,表面 上的力学作用(如摩擦或范性形变)或化学反应所导致的 电子发射。 前两种情形,可以完全在自由电子模型的范畴内得到 解释,其余的效应则相对复杂些,必须考虑电子和其它粒 子的相互作用才可解释
金属中的电子克服束缚跳出金属,根据其获得能量的方式 可以区分为: 1. 高温导致的热电子发射; 2. 强电场导致的场致发射; 3. 光照导致的光致发射: 4. 电子撞击产生的次级电子发射; 5. 表面上的放热反应导致的外激发射,或更一般地说,表面 上的力学作用(如摩擦或范性形变)或化学反应所导致的 电子发射。 前两种情形,可以完全在自由电子模型的范畴内得到 解释,其余的效应则相对复杂些,必须考虑电子和其它粒 子的相互作用才可解释

二、热电子发射: 实验表明,热电子发射的电流密度为 W j=AT2exp Richardson-Dushman公式 kgT 其中A为常数,W为功函数(或脱出功),即电子逸出金 属所需克服的势垒。 根据实验数据作图可以得到一条直线,其斜率给出功函数: 减) 对于该实验规律,金属自由电子论可以给出合理的解释
二、热电子发射: 实验表明,热电子发射的电流密度为 2 exp B W j AT k T æ ö = -ç ÷ è ø 其中A为常数,W为功函数(或脱出功),即电子逸出金 属所需克服的势垒。 Richardson-Dushman公式 根据实验数据作图可以得到一条直线,其斜率给出功函数: 2 1 ln j T T æ ö ç ÷ è ø : 对于该实验规律,金属自由电子论可以给出合理的解释

T=0时,所有电子的能量都不会超过费米能级:E 没有电子可以脱离金属。 T>0时,会有一些电子通过吸收热能获得高于V的能 量,逸出金属表面。 现在从自由电子模型出发推出热电子发射电流密度与温 度关系: h2k21 mw2,.v(k)= hk E(k)= 2 2m m 根据5.2节中给出的分析,系统在波矢空间dk体积内 的状态数为: ped,akd或=
T= 0 时,所有电子的能量都不会超过费米能级: 没有电子可以脱离金属。 T > 0 时,会有一些电子通过吸收热能获得高于V0的能 量,逸出金属表面。 现在从自由电子模型出发推出热电子发射电流密度与温 度关系: 0 EF 2 2 1 2 ( ) , ( ) 2 2 k k E k mv v k m m = = \ = h h Q 3 ( )d d d d d d 8 x y z x y z V r k k k k k k k p = 根据 5.2节中给出的分析,系统在波矢空间 体积内 的状态数为: 3 d k

各能级电子占有的几率应服从F-D公式: f(k)= E(k)-4 这里,化学势八可取作E +1 因此,单位体积内电子运动速度在 yx→vx+dvx,yy→Vy+dvy,y:→v+dv, 区同内的电子致日应为:dn=2气贸)dd,d如 设X方向垂直于金属表面,所以只有X方向上速度大于某一特 定值(即动能大于特定值)的电子方可逸出金属表面,即: 2 而对y和z方向电子的速度没有要求,可以是任意值
各能级电子占有的几率应服从F-D 公式: 1 ( ) ( ) exp 1 B f k E k k T m = æ ö - ç ÷ + è ø 这里,化学势 m 可取作 0 EF 因此,单位体积内电子运动速度在 d , d , d , x x x y y y zzz v ® v + v v ® v + v v ® + v v 区间内的电子数目应为: 3 3 1 d 2 ( )d d d 8 x y z m n f v v v v p æ ö = ç ÷ è ø h 设 x 方向垂直于金属表面,所以只有 x 方向上速度大于某一特 定值(即动能大于特定值)的电子方可逸出金属表面,即: 2 0 0 1 2 m x F v > + V B E W 0 2 x V v m ³ 而对 y 和 z 方向电子的速度没有要求,可以是任意值

所以热电子发射电流密度的理论表达式应为: j.=-∫ev,dn 要考虑单位时间内从金属内部可以到达 金属表面的那部分电子,所以乘Vx。 fv(v))dr.dw,udr. dv, m2-E9 +1 因为功函数的量级为几个eV,而一般温度下kT~meV 所以上式可以得到简化:
d x x j = - ev n ò ( ) 3 3 2 d d d 8 x x y z e m v f v v v p æ ö = - ç ÷ è ø ò h v 0 3 3 3 2 0 2 1 2 d d d 4 exp 1 x y z x V F m B m e v v v v mv E k T p ¥ ¥ ¥ -¥ -¥ = - × æ ö - ç ÷ + è ø ò ò ò h 所以热电子发射电流密度的理论表达式应为: 要考虑单位时间内从金属内部可以到达 金属表面的那部分电子,所以乘 vx 。 因为功函数的量级为 几个eV, 而一般温度下 所以上式可以得到简化: k TB : meV

j 9 于是得到: (见后面详细说明) "m到 (见黄昆书p288) —Richardson-Dushman公式 其中 4= 2π2h W='。-E9 在上面的推导中,用到两个积分公式:
( ) 2 0 0 2 3 exp 2 B F x B me k T V E j p k T æ ö - = - -ç ÷ è ø h 2 exp B W j AT k T æ ö \ = -ç ÷ è ø —— Richardson-Dushman公式 其中 2 2 3 2 m B ek A p = - h 0 W = - V E 0 F 在上面的推导中,用到两个积分公式: 0 3 0 2 3 3 2 d d exp exp d 4 2 F y z x x V B B m m e E mv v v v v p k T k T ¥ ¥ ¥ -¥ -¥ æ ö æ ö » - - ç ÷ ç ÷ è ø è ø ò ò ò h 于是得到: (见后面详细说明) (见黄昆书p288)