
3.3固体热容的量子理论 一. 经典理论的困难 二.爱因斯坦模型 (Einstein1907年) 三.德拜模型 (Debye1912年) 四.实际晶体的热容 参考:黄昆书3.8节(p122-132) Kittel书5.1节(79-87) 热容是固体原子热运动在宏观性质上的体现,因而对固体 原子热运动的认识实际上首先是从固体热容研究开始的
3.3 固体热容的量子理论 一. 经典理论的困难 二. 爱因斯坦模型(Einstein 1907年) 三. 德拜模型(Debye 1912年) 四. 实际晶体的热容 参考:黄昆书 3.8节(p122-132) Kittel 书 5.1节(79-87) 热容是固体原子热运动在宏观性质上的体现,因而对固体 原子热运动的认识实际上首先是从固体热容研究开始的

一.经典理论的困难 Dulong一Petit1819年发现大多数固体常温下的摩尔 热容量差不多都等于一个与材料和温度无关的常数值(25 J/mol.K),这个结果就称为Dulong一Petit定律。 根据经典统计中的能量均分定理,受简谐力作用的原子 像一组谐振子,每个自由度的平均总能量为kT,一摩尔固体 中有N,个原子,所以每摩尔晶体晶格的振动能为: E=3N kgT 3N kg=const. Cy=3×6.02217×1.38062J.mol.K-=24.9430J.mol1.K-1 虽然Dulong一Petit定律得到经典能量均分定理的解释。 但1875年Veber就发现不少固体的热容量远低于Dulong一 Petit数值,而且随温度的降低而减小,这是经典理论所无法 理解的
一. 经典理论的困难 Dulong-Petit 1819 年发现大多数固体常温下的摩尔 热容量差不多都等于一个与材料和温度无关的常数值(25 J/mol﹒K),这个结果就称为Dulong-Petit定律。 根据经典统计中的能量均分定理,受简谐力作用的原子 像一组谐振子,每个自由度的平均总能量为 kBT,一摩尔固体 中有 个原子,所以每摩尔晶体晶格的振动能为: 3 E NA B = k T 3 const. V A B V E C N k T æ ö ¶ \ = ç ÷ = = ¶è ø 虽然Dulong-Petit 定律得到经典能量均分定理的解释。 但1875年Weber 就发现不少固体的热容量远低于Dulong- Petit数值,而且随温度的降低而减小,这是经典理论所无法 理解的。 NA -1 1 -1 1 CV 3 6.02217 1.38062J mol K 24.9430J mol K - - = ´ ´ × × = × ×
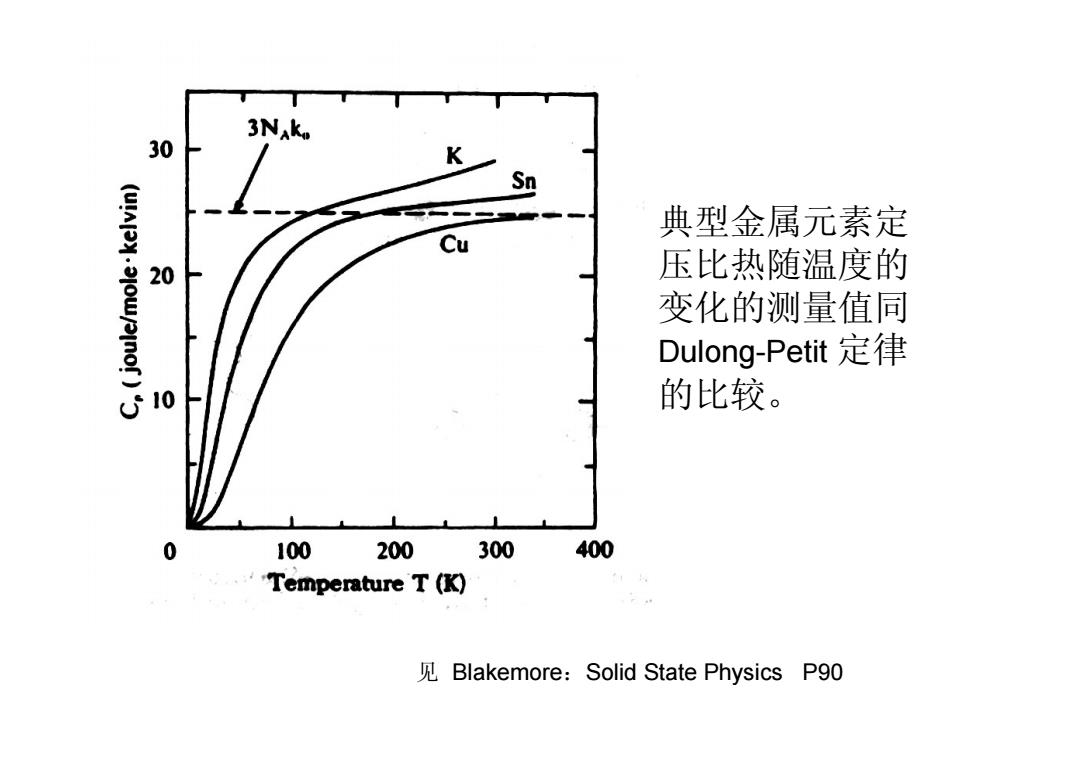
3Nako 30 K Sn 典型金属元素定 Cu 20 压比热随温度的 变化的测量值同 Dulong-Petit定律 10 的比较。 0 100 200 300 400 'Temperature T(K) Blakemore:Solid State Physics P90
见 Blakemore:Solid State Physics P90 典型金属元素定 压比热随温度的 变化的测量值同 Dulong-Petit 定律 的比较

二.Einstein模型 1907年Einstein用量子论解释了固体热容随温度下降的 事实,这是1905年Einstein首次用量子论解释光电效应后, 量子论的又一巨大成功。 Einstein保留了原子热振动可以用谐振子描述的观点,但 放弃了能量均分的经典观念,而假定其能量是量子化的: 6,=(n,+)h@, 在与环境温度处于热平衡状态时谐振子按时间的平均能量为: ho 当kT>ho,时,即高温下:8,=kI hoi 和经典理论是一致的,只是在低温下 量子行为才是突出的
二. Einstein 模型 在与环境温度处于热平衡状态时谐振子按时间的平均能量为: 1907年 Einstein 用量子论解释了固体热容随温度下降的 事实,这是1905 年 Einstein 首次用量子论解释光电效应后, 量子论的又一巨大成功。 Einstein 保留了原子热振动可以用谐振子描述的观点,但 放弃了能量均分的经典观念,而假定其能量是量子化的: 1 ( ) 2 i i i e w = + n h 1 i B i i k T e w w e = - h h 当 时,即高温下: 和经典理论是一致的,只是在低温下 量子行为才是突出的。 B i k T >> hw i B e = k T

为确定谐振子的平均能量,Einstein.又做了一个极为简单 的假定,他假定晶体中所有原子都以同一频率o在振动。因 而在一定温度下,由N个原子组成的晶体的总振动能为: 3N 3N h0; ≥3W 九0E i=l exp hog kgT) exp 于是,( y= kgT 定义:Einstein温度 hoE TE= 可以通过和实验曲线的 kB 拟合确定具体数值
为确定谐振子的平均能量, Einstein又做了一个极为简单 的假定,他假定晶体中所有原子都以同一频率 wE在振动。因 而在一定温度下,由N个原子组成的晶体的总振动能为: 3 exp 1 E E B N k T w æ ö w ç ÷ - è ø h ; h 3 3 1 1 1 i B N N i i i i k T E e w w e = = = = - å å h h 2 2 exp 3 exp 1 E E B V B B E B E k T C Nk T k T k T w w w æ ö ç ÷ ¶ æ ö è ø = = × ç ÷ ¶ è ø é ù æ ö ê ú ç ÷ - ë û è ø h h h 于是, 定义:Einstein温度 E E B T k w = h 可以通过和实验曲线的 拟合确定具体数值

Cy =3Nkg TE (eT-1)2 )称作Einstein热容函数,它是温度的函数: 高温下:T>TE Tr/Thoe 谐振子处于高激发态,飞T比量子阶梯大的多,振动谱的 量子性质变得不那么重要了,就是经典理论描述的结果
高温下:T >> TE 2 2 3 3 ( ) ( 1) E E T T E E V B T B E T T e T C Nk Nk f T T e æ ö = = ç ÷ è ø - ( ) 称作Einstein热容函数,它是温度的函数: E E T f T / 1 T T E > hw ( x <<1) B k T

在低温下:T>1 Cy-3Nkp 很显然,表达式中指数项起主要作用,温度下降,热容量 降低。当T→0时,Cv→0,这与实验结果定性符合。但更 精细的实验结果表明,当温度很低时,Cv∝T,这说明 Einstein?理论假定单一频率是过分简单了。因此才促使 Bor等人开始了晶格振动的仔细研究,给出频率表达式。 尽管模型仍有不足之处,但Einstein使用一个可调参数 T(⊙E)就可以基本解释热容一温度关系的做法应当看作是 理论物理工作的一个典范之作。这充分说明,能量量子化 才是理解晶格振动问题的关键,这也间接印证了提出用声 子概念讨论晶体性质的必要性
在低温下:T > 2 3 TE E T V B T C Nk e T - æ ö = ç ÷ è ø 尽管模型仍有不足之处, 但 Einstein使用一个可调参数 TE (ωE)就可以基本解释热容-温度关系的做法应当看作是 理论物理工作的一个典范之作。这充分说明,能量量子化 才是理解晶格振动问题的关键,这也间接印证了提出用声 子概念讨论晶体性质的必要性

25 Classical 金刚石比热测量值 20 与Einstein模型给出 Einstein 结果的比较。 15 10 TE=1320K 5 0.0.0( Q 0 0.2 0.4 0.6 0.8 .1.0 T1320)=(TT) Blakemore:Solid State Physics P121 黄昆书(P125图3一21)
见 Blakemore:Solid State Physics P121 黄昆书 (P125 图3-21) 金刚石比热测量值 与Einstein模型给出 结果的比较。 TE = 1320K

三.Debye模型: Debye(1912)修正了原子是独立谐振子的概念,而考 虑晶格的集体振动模式,他假设晶体是各向同性的连续弹性 介质,原子的热运动以弹性波的形式发生,每一个弹性波振 动模式等价于一个谐振子,能量是量子化的,并规定了一个 弹性波频率上限OD,称之为德拜频率。 因为由N个原子组成的晶体其自由度为3N,所以只能有 3N种振动模式,故: OD g(@)do 3N 代入弹性波的态密度:g(o)= 3V@2 2π2v 即可确定德拜频率数值: 其中n是单位体积原子数
三.Debye 模型: Debye(1912)修正了原子是独立谐振子的概念,而考 虑晶格的集体振动模式,他假设晶体是各向同性的连续弹性 介质,原子的热运动以弹性波的形式发生,每一个弹性波振 动模式等价于一个谐振子,能量是量子化的,并规定了一个 弹性波频率上限 ,称之为德拜频率。 因为由 N 个原子组成的晶体其自由度为 3N,所以只能有 3N 种振动模式,故: wD 0 ( )d 3 D g N w w w = ò 代入弹性波的态密度: ( ) 2 2 3 3 2 s V g v w w p = 即可确定德拜频率数值: 其中n是单位体积原子数。 ( ) 1 2 3 1 3 2 3 6 6 s D s N v n v V p w p æ ö = = ç ÷ è ø

德拜频率OD是一个十分有用的参数,它的直接意 义是在弹性波近似下,晶格振动的最高频率。与此相关我 们还可以定义德拜温度和德拜半径: Tp= hop kg 9D= =(6mn)月 Vs 在德拜模型下: 3N 3N E- ho-f g(o) ho h ho do i=1 i=l aT-1 修订了Einstein.单一振动频率的假定,求和变积分, 代入弹性波态密度表达式后,即可给出:
德拜频率 是一个十分有用的参数,它的直接意 义是在弹性波近似下,晶格振动的最高频率。与此相关我 们还可以定义德拜温度和德拜半径: ( ) 1 2 3 6 D D s q n v w = = p wD D D B T k w = h 在德拜模型下: 3 3 0 1 1 ( ) d 1 1 D i B B N N i i i i k T k T E g e e w w w w w e w w = = = = = - - å å h h ò h h 修订了Einstein单一振动频率的假定,求和变积分, 代入弹性波态密度表达式后,即可给出: