
5.7晶体能带的对称性 E()函数的对称性 二.E图示 三.空格模型的能带 见黄昆书4.6节p202 晶体具有对称性,因而晶体中电子的运动状态也会具 有对称性,所以表述运动状态的本征能量和本征态也具有 对称性,了解了这种对称性,对于我们理解能带性质、简 化要处理的问题会很有帮助。比如在计算和绘制k空间的 能带图时,就可以充分利用其对称性质。 晶体的对称性包括点对称操作和平移对称性,它们都 会反映到本征能量的对称性上。 晶体能带的对称性和晶格振动色散关系所具有的对称 性相同,我们可以参照理解
5.7 晶体能带的对称性 晶体具有对称性,因而晶体中电子的运动状态也会具 有对称性,所以表述运动状态的本征能量和本征态也具有 对称性,了解了这种对称性,对于我们理解能带性质、简 化要处理的问题会很有帮助。比如在计算和绘制 k 空间的 能带图时,就可以充分利用其对称性质。 晶体的对称性包括点对称操作和平移对称性,它们都 会反映到本征能量的对称性上。 晶体能带的对称性和晶格振动色散关系所具有的对称 性相同,我们可以参照理解。 一. En (k)函数的对称性 二. En (k)图示 三. 空格模型的能带 见黄昆书 4.6节 p202

一、 E()函数的对称性 1.E(k)=E(+G) 平移对称性 Bloch定理一节中曾指出简约波矢k表示原胞之间电 子波函数位相的变化,如果飞改变一个倒格矢量,它们 所标志的原胞之间波函数位相的变化是相同的,也就是 说k和k+G是等价的,从这点出发我们也可认为E,(k) 是k空间的周期函数,其周期等于倒格矢。简约波矢的 取值范围就是倒易空间的Wigner-Seitz.原胞,即第一布里 渊区内。我们利用这种平移对称性可以将第二Brillouin区 的每一块各自平移一个倒格矢而与第一Brillouinl区重合。 同理,更高的Brillouin区也可通过适当的平移与第一区重 合,因此我们可以把注意力仅限制在第一区内,它包含 了晶体能带的所有必要信息。 应特别注意,这个表达式只是对同一能带才正确
一、 En (k)函数的对称性 Bloch定理一节中曾指出简约波矢 k 表示原胞之间电 子波函数位相的变化,如果 k 改变一个倒格矢量,它们 所标志的原胞之间波函数位相的变化是相同的,也就是 说 k 和 k+Gh 是等价的,从这点出发我们也可认为 是 k 空间的周期函数,其周期等于倒格矢。简约波矢的 取值范围就是倒易空间的Wigner-Seitz原胞,即第一布里 渊区内。我们利用这种平移对称性可以将第二Brillouin区 的每一块各自平移一个倒格矢而与第一Brillouin区重合。 同理,更高的Brillouin区也可通过适当的平移与第一区重 合,因此我们可以把注意力仅限制在第一区内,它包含 了晶体能带的所有必要信息。 应特别注意,这个表达式只是对同一能带才正确。 ( ) ( ) n n Gh E k E k v v v 1. = + E k n ( ) 平移对称性
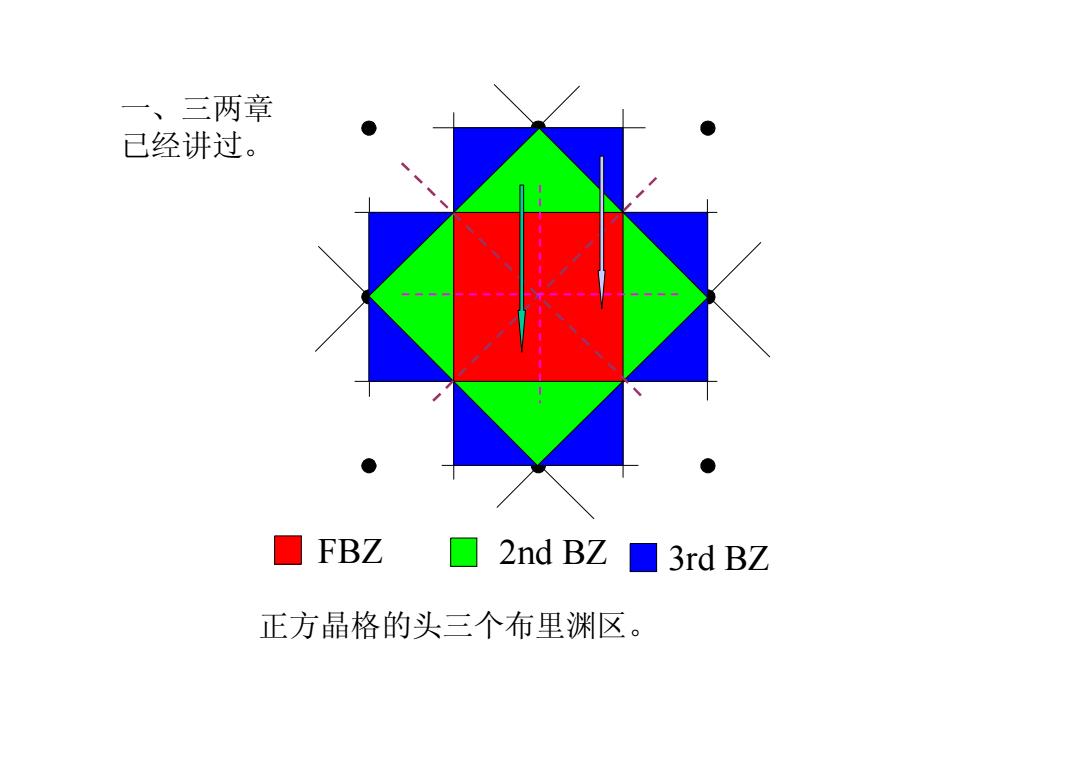
一、三两章 已经讲过。 ■FBZ ☐2ndBZ3rdBZ 正方晶格的头三个布里渊区
Simple Cubic Lattice, FBZ; 2nd BZ; 3rd BZ FBZ 2nd BZ 3rd BZ 正方晶格的头三个布里渊区。 一、三两章 已经讲过
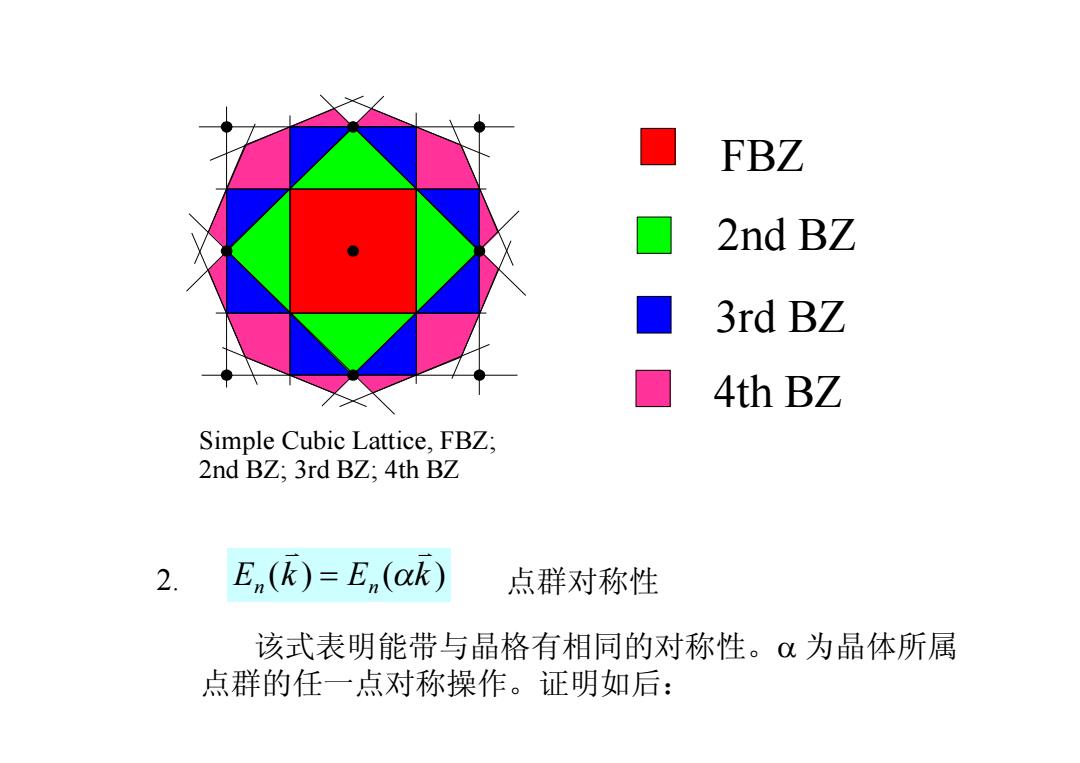
FBZ 2nd BZ 0 3rd BZ ☐4thBZ Simple Cubic Lattice,FBZ: 2nd BZ:3rd BZ:4th BZ 2. E,(k=E,(ak) 点群对称性 该式表明能带与晶格有相同的对称性。α为晶体所属 点群的任一点对称操作。证明如后:
E (k ) E ( k ) n n v v = a 该式表明能带与晶格有相同的对称性。a 为晶体所属 点群的任一点对称操作。证明如后: 2. 点群对称性 Simple Cubic Lattice, FBZ; 2nd BZ; 3rd BZ; 4th BZ FBZ 2nd BZ 3rd BZ 4th BZ

设Ψ(r)为晶体哈密顿量的本征函数,本征值为E(k)。 iyk(F)=En(k)Wk(F) 由于晶体在所属点群操作下保持不变,则点群操作α作用 于本征函数的结果, φn(F)=ynk(0r) 应为具有同样本征值的另一本征函数。 W(aF+aR)=eakn(aF) 又由于晶体点群操作应保持点乘积不变,则有: A·B=(A·B)=A·B a1A.B=OoA·CB=AB
应为具有同样本征值的另一本征函数。 设 ynk(r)为晶体哈密顿量的本征函数,本征值为 En (k)。 ( ) ( ) ( ) ˆH r E k r nk n nk v v v y = y 由于晶体在所属点群操作下保持不变,则点群操作a作用 于本征函数的结果, (r) ( r) n nk v v f =y a ( r R ) e ( r) nk ik R nk n n v v v v v y a a y a ×a + = A B A B A B A B A B A B v v v v v v v v v v v v a a a a a a a a × = × = × × = × = × -1 -1 ( ) 又由于晶体点群操作应保持点乘积不变,则有:

因此有: ,(F+瓦)=yk[o(F+R〗=eayk(r) =(a) 所以中)的波矢标记应该是: a-'k 中(r)是本征函数之一,所以可以写成: Wna(F) 从而有: Ψnak(F)=Ψk(0T)
因此有: ( ) ( ) [ ( )] ( ) 1 e r r R r R e r nk i k R nk ik R n n nk n n n v v v v v v v v v v y a f y a y a a a × × - = + = + = fn (r)是本征函数之一,所以可以写成: 所以 fn (r) 的波矢标记应该是: k -1 a 1 (r) n k v - a y 从而有: 1 (r) ( r) nk n k v v y y a a - =

从上式可得有k和飞所对应的能量本征值相等, 即有: E(a'k)=E(k) 由于1遍历晶体点群的所有的对称操作,所以有: E(k)=E(ak) 证毕。 这表明,在k空间中Ek具有与晶体点群完全相同 的对称性。这样就可以在晶体能带计算和表述中把第 一布里渊区分成若干个等价的小区域,只取其中一个 就足够了。区域大小为第一布里渊区的1f,为晶体 点群对称操作元素数。如三维立方晶体f=48。 原胞是晶体点阵的最小重复单位,因此点阵具有的点群 对称性全部反映在原胞中是能够理解的
从上式可得有 a-1k 和 k 所对应的能量本征值相等, 即有: ( ) ( ) 1 E k E k n n v v = - a E (k ) E ( k ) n n v v = a 由于a-1遍历晶体点群的所有的对称操作,所以有: 证毕。 这表明,在 k 空间中 En (k) 具有与晶体点群完全相同 的对称性。这样就可以在晶体能带计算和表述中把第 一布里渊区分成若干个等价的小区域,只取其中一个 就足够了。区域大小为第一布里渊区的 1/f,f 为晶体 点群对称操作元素数。如三维立方晶体 f = 48。 原胞是晶体点阵的最小重复单位,因此点阵具有的点群 对称性全部反映在原胞中是能够理解的

3.E,(k)=E(-k) 反演对称性 在晶体中电子运动的哈密顿算符 H=- r+in 是实算符,H=H。 如果以(r)是方程的解,那么wn(r)也是方程的解, 且这两个解具有相同的能量本征值。即有 Hwn(F)=E(k)w nk(F Hwk(F)=E(knk()
在晶体中电子运动的哈密顿算符 ( ) 2 2 2 H U m = - Ñ + h r 是实算符,H* =H。 如果 ynk (r) 是方程的解,那么 y * nk (r) 也是方程的解, 且这两个解具有相同的能量本征值。即有 3. E (k ) E ( k ) n n v v = - ( ) ( ) ( ) ˆ ( ) ( ) ( ) ˆ H r E k r H r E k r nk n nk nk n nk v v v v v v * * = = y y y y 反演对称性

同时按照Bloch定理有: y(F+Rn)=e-Ry4(下) Ψn-k(下+厄n)=eRyn-k(F) 因此,以(r)和ynk()能量是相同的。 E(k)=E(-k) 这个结论不依赖于晶体的点群对称性,不管晶体中是否 有对称中心,在k空间中E,()总是有反演对称的。这 实际上是时间反演对称性的结果。 下面通过对具体对象的讨论来理解和应用能带的对称性
同时按照Bloch定理有: ( ) ( ) ( ) ( ) r R e r r R e r n k ik R n k n nk ik R nk n n n v v v v v v v v v v - - × - * - × * + = + = y y y y 因此,ynk (r) 和yn-k (r) 能量是相同的。 E (k ) E ( k ) n n v v = - 这个结论不依赖于晶体的点群对称性,不管晶体中是否 有对称中心,在 k 空间中 En (k) 总是有反演对称的。这 实际上是时间反演对称性的结果。 下面通过对具体对象的讨论来理解和应用能带的对称性
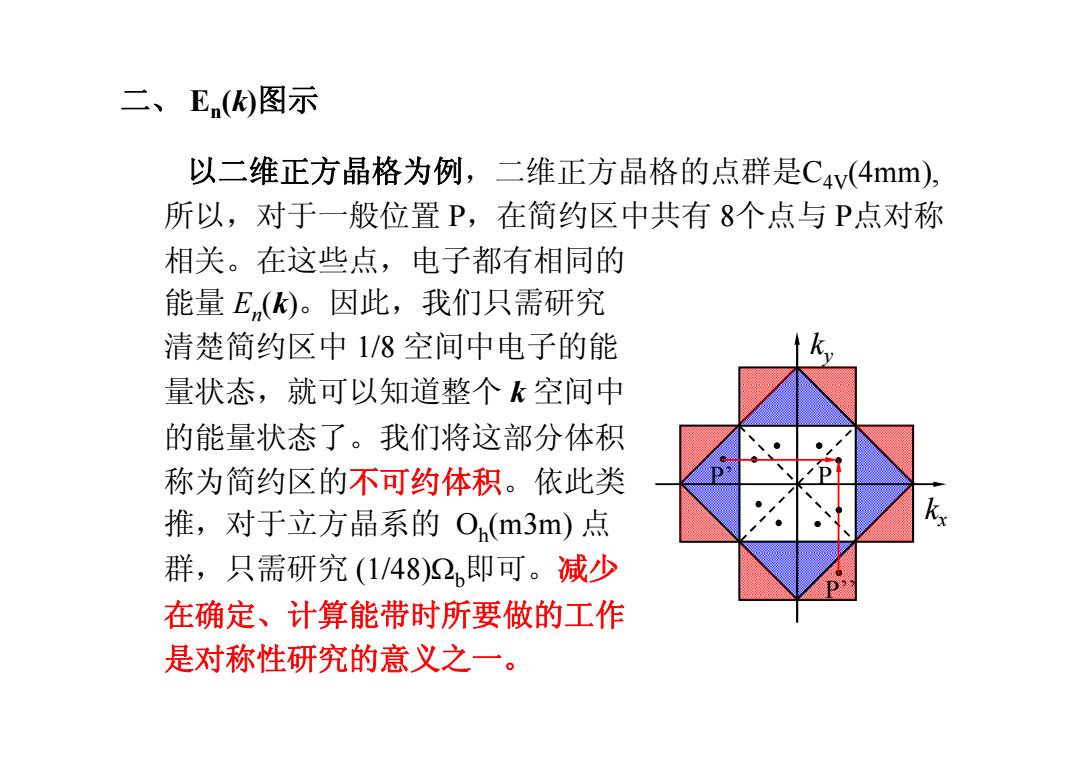
二、E图示 以二维正方晶格为例,二维正方晶格的点群是C4v(4mm), 所以,对于一般位置P,在简约区中共有8个点与P点对称 相关。在这些点,电子都有相同的 能量E(k)。因此,我们只需研究 清楚简约区中1/8空间中电子的能 量状态,就可以知道整个k空间中 的能量状态了。我们将这部分体积 称为简约区的不可约体积。依此类 推,对于立方晶系的O,(m3m)点 群,只需研究(1/48)2即可。减少 在确定、计算能带时所要做的工作 是对称性研究的意义之一
P P’’ P’ kx ky 以二维正方晶格为例,二维正方晶格的点群是C4V(4mm), 所以,对于一般位置 P,在简约区中共有 8个点与 P点对称 相关。在这些点,电子都有相同的 能量 En (k)。因此,我们只需研究 清楚简约区中 1/8 空间中电子的能 量状态,就可以知道整个 k 空间中 的能量状态了。我们将这部分体积 称为简约区的不可约体积。依此类 推,对于立方晶系的 Oh (m3m) 点 群,只需研究 (1/48)Wb即可。减少 在确定、计算能带时所要做的工作 是对称性研究的意义之一。 二、 En (k)图示