
5.3三维周期场中电子运动的近自由电子近似 一、方程与微扰计算 方程: [p+io-w 周期场:U(r)=U(r+R) R为格矢 Fourier展开:U(r)=U,+∑Uneo,r n≠0 U,=U()dr势能函数的平均值 U.=wU()e,dr微小量
5.3 三维周期场中电子运动的近自由电子近似 一、方程与微扰计算 ( ) ( ) ( ) 2 2 2 U E m y y é ù - Ñ + = ê ú ë û h 方程: r r r 周期场: U U ( ) = + ( ) l r r R Rl 为格矢 Fourier展开: ( ) 0 0 n i n n U U U e × ¹ = +å G r r ( ) 0 ( ) 1 V U U d V = t ò r 势能函数的平均值 ( ) ( ) 1 n i n V U U e d V t - × = ò G r r 微小量

H=- 0() 2m 2m =H。+H' 零级近似:H,= 令U。=0 2m 微扰项: H'=∑.eiG.r n≠0 可由自由电子求出零级近似的归一化波函数和能量本征值 方2k2 E(k)= 2m )e
( ) 2 2 2 2 0 2 2 0 n i n n H U U U e m m × ¹ = - Ñ + = - Ñ + +å h h G r r H H 0 = + ¢ 2 2 2 2 0 0 2 2 H U m m = - Ñ + = - Ñ h h 零级近似: 0 令U = 0 微扰项: 0 n i n n H U e × ¹ ¢ = å G r 可由自由电子求出零级近似的归一化波函数和能量本征值 ( ) 2 2 (0) 2 k E m = h k ( ) (0) 1 i e V y × = k r k r

与一维情况类似,一级微扰能量为 E((k=k H'k plu.d 一级修正的波函数和二级微扰能量分别为 a四w (K'H'\k) 24 2mUn ze(+G,)r 因-名长x妆a 2mU
与一维情况类似,一级微扰能量为 ( ) (1) E H k = k k¢ ( ) 0 1 0 n i i i n V n e U e e d V t - × × × ¹ æ ö = = ç ÷ è ø ò å k r G r k r 一级修正的波函数和二级微扰能量分别为 ( ) ( ) ( ) ( ) (1) (0) (0) (0) H E E y y ¢ ¢¹ ¢ ¢ = å - ¢ k k k k k k r r k k ( ) ( ) 2 2 2 2 0 1 2 n n i n n mU e V k + × ¹ = - + åh h k G r k G ( ) ( ) ( ) ( ) 2 2 (2) (0) (0) 2 2 2 2 0 2 n n n H m U E ¢¹ ¹ E E k ¢ ¢ = = - ¢ - + å å k k h h k k k k k k G

其中 kHr"k=ekr∑Ue'd n≠0 当k=k十Gn 当k≠k+Gn 当k离布里渊区边界较远时,由于周期场的影响而 产生的各散射波成分的振幅都很小,可以看成小的微扰。 但是,在布里渊区边界面上或其附近时,即当k2=(k+G)2 时,这时相应的散射波成分的振幅变得很大,不能当作 小的微扰来处理,而要用简并微扰来处理。 零级近似的波函数由相互作用强的几个态的线性组 合来组成,由此可解得在布里渊区边界面上简并分裂后 的能量为 E生=Eo(k)±Un
其中 ( ) ( ) 0 1 n i i n V n H e U e d V t - ¢- × × ¹ ¢ ¢ = ò å k k r G r k k ={ 0 Un 当 k’=k+Gn 当 k’ ¹ k+Gn 当 k 离布里渊区边界较远时,由于周期场的影响而 产生的各散射波成分的振幅都很小,可以看成小的微扰。 但是,在布里渊区边界面上或其附近时,即当k 2@(k+Gn ) 2 时,这时相应的散射波成分的振幅变得很大,不能当作 小的微扰来处理,而要用简并微扰来处理。 零级近似的波函数由相互作用强的几个态的线性组 合来组成,由此可解得在布里渊区边界面上简并分裂后 的能量为 ( ) (0) E± = ± E Un k
需要指出的是,在三维情况下,在布里渊区边界面上的 一 般位置,电子的能量是二重简并的,即有两个态的相互作 用强,其零级近似的波函数就由这两个态的线性组合组成: 而在布里渊区边界的棱边上或顶点上,则可能出现能量多重 简并的情况。对于g重简并,即有g个态的相互作用强,因 而,其零级近似的波函数就需由这g个相互作用强的态的线 性组合组成,由此解出简并分裂后的g个能量值。 k k3 长6 ks
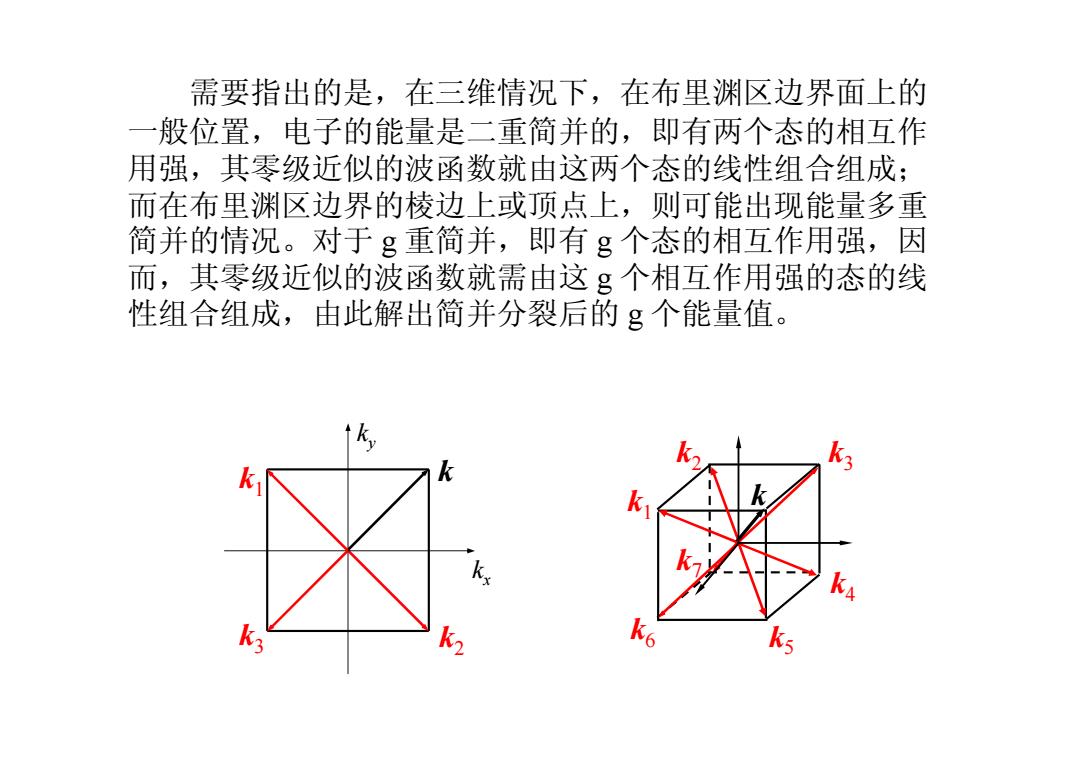
需要指出的是,在三维情况下,在布里渊区边界面上的 一般位置,电子的能量是二重简并的,即有两个态的相互作 用强,其零级近似的波函数就由这两个态的线性组合组成; 而在布里渊区边界的棱边上或顶点上,则可能出现能量多重 简并的情况。对于 g 重简并,即有 g 个态的相互作用强,因 而,其零级近似的波函数就需由这 g 个相互作用强的态的线 性组合组成,由此解出简并分裂后的 g 个能量值。 k k 1 k2 k3 k k2 k3 k1 k4 k5 k6 k k7 x ky

二、布里渊区与能带 引入周期性边界条件后,在k空间中,波矢k的取 值不连续,k的取值密度为 V p(K)= 8元 V为晶体体积 而简约区的体积=倒格子原胞体积=2 简约区中k的取值总数=pk)2,=N=晶体原胞数 每一个k确定一个电子能级,根据Pauli原理,每一 个能级可以填充自旋相反的两个电子。因此,简约区中 共可填充2N个电子。 由于每一个布里渊区的体积都等于倒格子原胞体积 2,所以,每一个布里渊区都可以填充2N个电子
二、布里渊区与能带 引入周期性边界条件后,在k空间中,波矢k的取 值不连续,k的取值密度为 ( ) 3 8 V r p k = V为晶体体积 而简约区的体积=倒格子原胞体积= Wb 简约区中 k 的取值总数=r(k) Wb =N=晶体原胞数 每一个 k 确定一个电子能级,根据 Pauli 原理,每一 个能级可以填充自旋相反的两个电子。因此,简约区中 共可填充 2N 个电子。 由于每一个布里渊区的体积都等于倒格子原胞体积 Wb,所以,每一个布里渊区都可以填充 2N 个电子
1.En()函数的三种图象 在k空间中,电子能量E,()函数有三种不同的表示 方式,称为三种布里渊区图象。这三种表示方法是等价 的,可根据所考虑问题的方便选择不同的表示方法。 若波矢量k在整个k空间中取值,这时每一个布里渊 区中有一个能带,第n个能带在第n个布里渊区中,这种 表示法称为扩展的布里渊区图象。 Ⅲ Ⅲ Ⅲ -2 0 a 3开
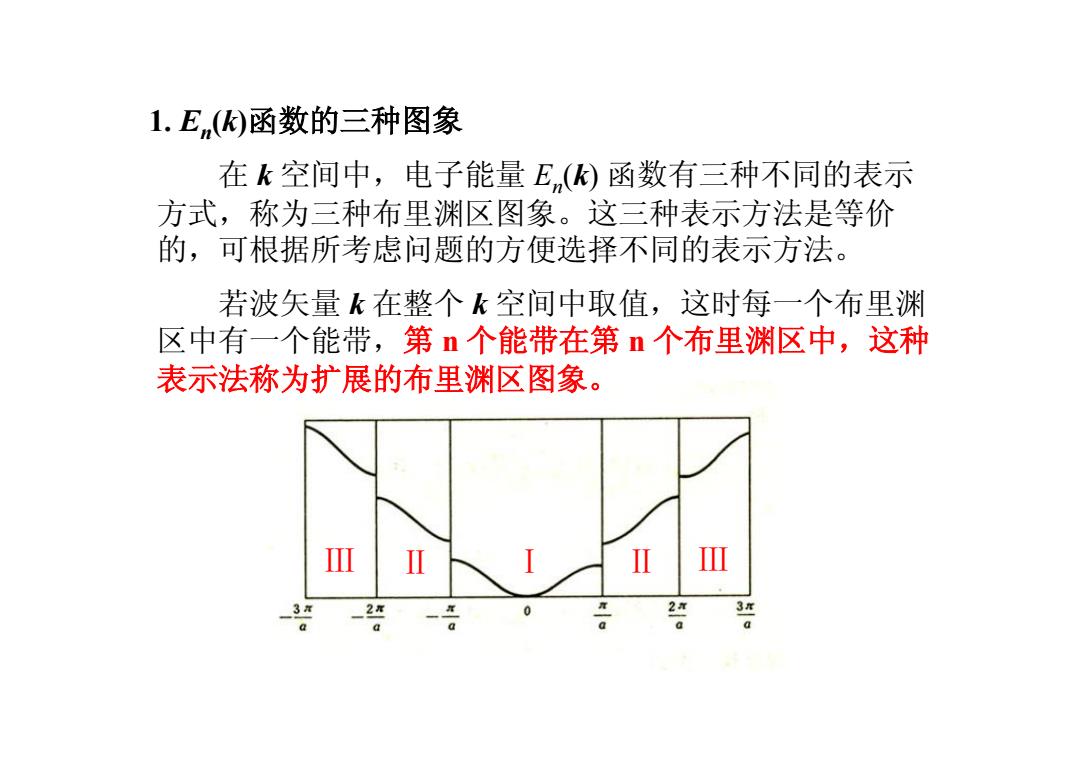
1. En (k)函数的三种图象 在 k 空间中,电子能量 En (k) 函数有三种不同的表示 方式,称为三种布里渊区图象。这三种表示方法是等价 的,可根据所考虑问题的方便选择不同的表示方法。 若波矢量 k 在整个 k 空间中取值,这时每一个布里渊 区中有一个能带,第 n 个能带在第 n 个布里渊区中,这种 表示法称为扩展的布里渊区图象。 Ⅲ Ⅱ Ⅰ Ⅱ Ⅲ

若将波矢量k限制在简约区中,由于k和k+G,所对应的平 移算符本征值相同,也就是说,k和k+G标志的原胞间电 子波函数的位相变化相同。在这个意义上,可以认为k和 k+G是等价的。因此,可以将k限制在简约区中。但是 由于电子的能量分为 若干个能带,如将所 带3 有能带都表示在简约 区中,那么,对于一 个简约波矢k,就有若 干个分立的能量值与 之对应。我们用n来区 带2 分不同的能带E(k)。 对于给定的能带n, 带 E(k)是k的连续函数
若将波矢量 k 限制在简约区中,由于 k 和k+Gl所对应的平 移算符本征值相同,也就是说,k 和 k+Gl标志的原胞间电 子波函数的位相变化相同。在这个意义上,可以认为 k 和 k+Gl是等价的。因此,可以将 k 限制在简约区中。但是 由于电子的能量分为 若干个能带,如将所 有能带都表示在简约 区中,那么,对于一 个简约波矢 k,就有若 干个分立的能量值与 之对应。我们用 n来区 分不同的能带 En (k)。 对于给定的能带 n, En (k)是 k的连续函数。 Ⅲ Ⅱ Ⅰ Ⅱ Ⅲ
E()的这种表示法称为简约布里渊区图象。实际上,由于 我们认为k和+G,等价,因而,E(k)的简约布里渊区图象 中的第n个能带,实际上是由扩展布里渊区图象中从第n 个布里渊区中平移一个倒格矢G,而得来的。 由于认为k和什G,等价,因而可以认为E(k)是k空 间中以倒格矢G为周期的周期函数,即E(k)=E(k十G)。 而简约布里渊区是倒易空间的原胞,以此原胞为重复单 元进行平移操作可 以得到整个k空 间,这些单元都是 等价的。因此,对 于同一能带有: E(k)=E(k十G) 3-2 0
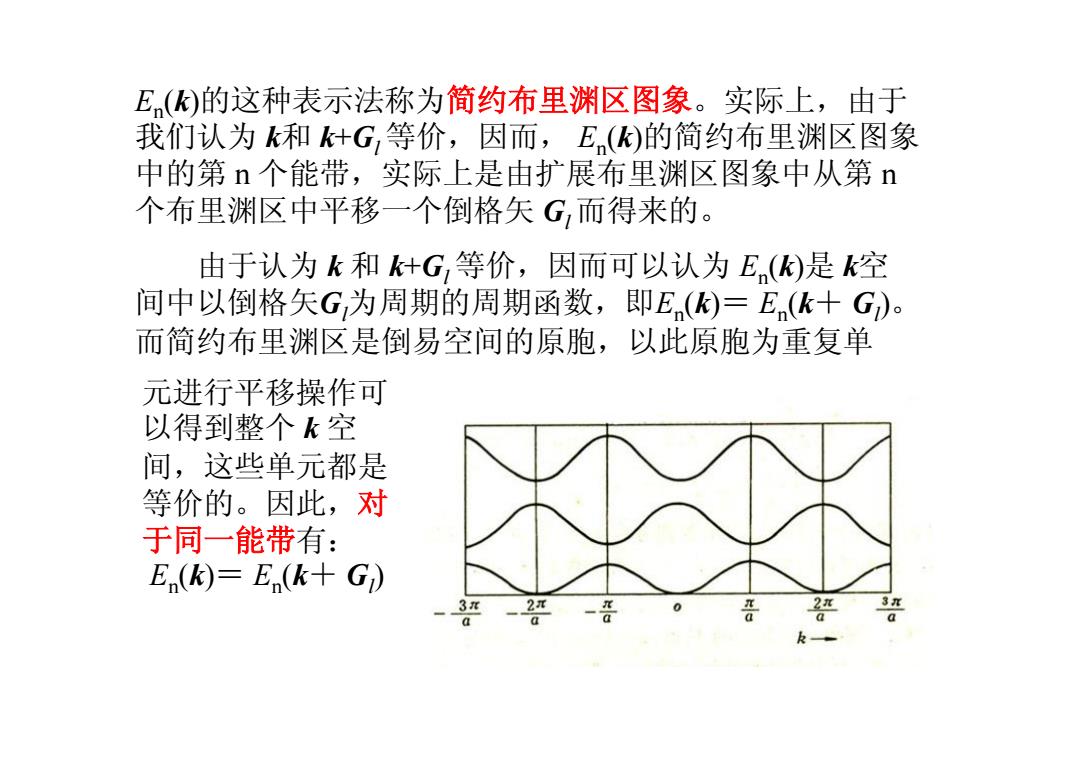
En (k)的这种表示法称为简约布里渊区图象。实际上,由于 我们认为 k和 k+Gl 等价,因而, En (k)的简约布里渊区图象 中的第 n 个能带,实际上是由扩展布里渊区图象中从第 n 个布里渊区中平移一个倒格矢 Gl 而得来的。 由于认为 k 和 k+Gl 等价,因而可以认为 En (k)是 k空 间中以倒格矢Gl为周期的周期函数,即En (k)= En (k+ Gl )。 而简约布里渊区是倒易空间的原胞,以此原胞为重复单 元进行平移操作可 以得到整个 k 空 间,这些单元都是 等价的。因此,对 于同一能带有: En (k)= En (k+ Gl )
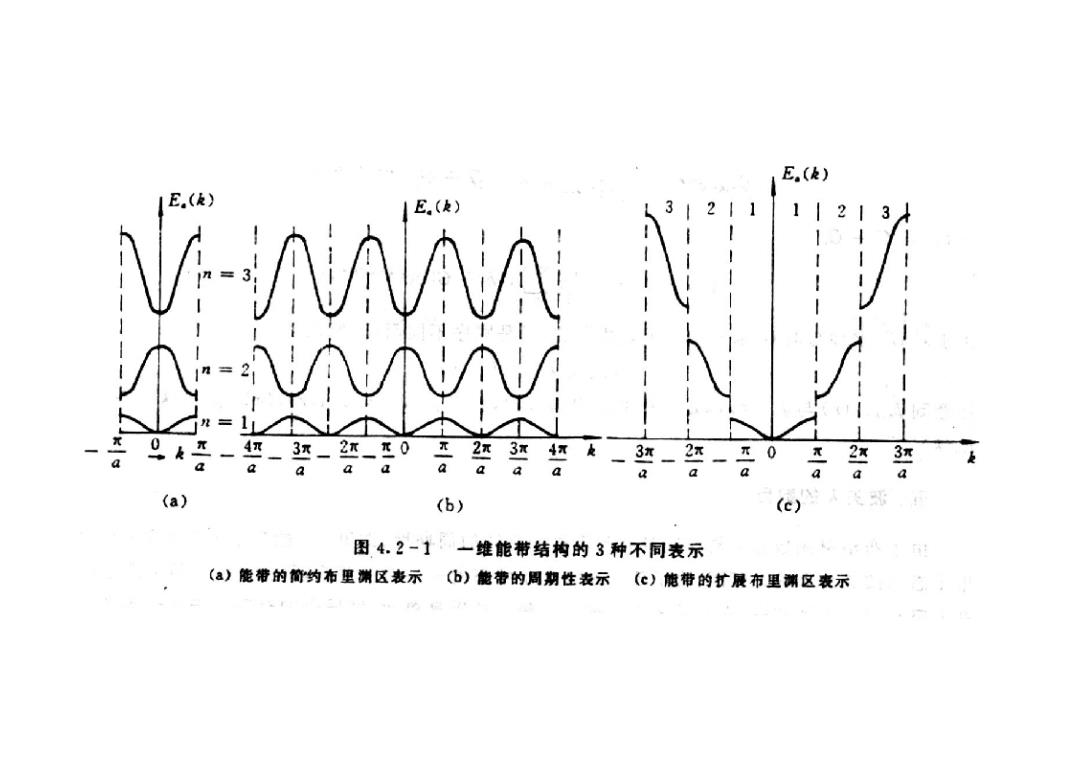
E.(k) E.(k) 1E.(k) 3 211 1121 3 V-NNNN N-VNM a Q aaa 3-2-0不2 3 a aa a a (a) (b) (c) 图4.2-1一维能特结构的3种不同表示 (a)能带的简约布里渊区表示(b)能带的周期性表示(©)能带的扩展布里渊区表示