
1.2晶体的对称性:晶系,点群,空间群 一.对称性的概念 二.晶体中允许的对称操作 三.晶体宏观对称性的表述:点群 四.七个晶系和14种晶体点阵 五.晶体的微观对称性:空间群 六.点群对称性和晶体的物理性质 参考:黄昆书1.5-1.7节 阎守胜2.2节 ·除去晶体点阵外,晶体的结构还能够用什么样 的语言方便地描述?
1.2 晶体的对称性:晶系,点群,空间群 一 . 对称性的概念 二. 晶体中允许的对称操作 三. 晶体宏观对称性的表述:点群 四. 七个晶系和14种晶体点阵 五. 晶体的微观对称性:空间群 六. 点群对称性和晶体的物理性质 参考:黄昆 书 1.5-1.7 节 阎守胜 2.2 节 • 除去晶体点阵外,晶体的结构还能够用什么样 的语言方便地描述?

一.对称性的概念: 一个物体(或图形)具有对称性,是指该物 体(或图形)是由两个或两个以上的部分组成, 经过一定的空间操作(线性变换),各部分调换 位置之后整个物体(或图形)保持不变的性质。 对称操作:维持整个物体不变而进行的操作称作对 称操作。即:操作前后物体任意两点间的距离保持 不变的操作。 点对称操作:在对称操作过程中至少有一点保持不动 的操作。有限大小的物体,只能有点对称操作。 对称元素:对称操作过程中保持不变的几何要素: 点,反演中心;线,旋转轴;面,反映面等
对称操作:维持整个物体不变而进行的操作称作对 称操作。即:操作前后物体任意两点间的距离保持 不变的操作。 点对称操作:在对称操作过程中至少有一点保持不动 的操作。有限大小的物体,只能有点对称操作。 对称元素:对称操作过程中保持不变的几何要素: 点,反演中心;线,旋转轴;面,反映面等。 一.对称性的概念: 一个物体(或图形)具有对称性,是指该物 体(或图形)是由两个或两个以上的部分组成, 经过一定的空间操作(线性变换),各部分调换 位置之后整个物体(或图形)保持不变的性质

一些图形的对称操作: (a)圆 (b)正方形 (c)等腰梯形 (d)不规则四边形 对称形不同的几种图形 如何概括和区别四种图形的对称性? 从旋转来看,圆形对绕中心的任何旋转都是不变的;正方形 只能旋转 才保持不变;后2个图形只有2π的旋转。 圆形的任一直径都是对称线;正方形只有4条连线是对称线; 等腰梯形只有两底中心连线是对称线
一些图形的对称操作: ● ● 如何概括和区别四种图形的对称性? 从旋转来看,圆形对绕中心的任何旋转都是不变的;正方形 只能旋转 才保持不变;后 2个图形只有 的旋转。 圆形的任一直径都是对称线;正方形只有 4条连线是对称线; 等腰梯形只有两底中心连线是对称线。 3 , , 2 2 π π π 2 π

以上,考察在一定几何变换之下物体的不变性,使 用的几何变换(旋转和反射)都是正交变换一 保持 两点距离不变的变换: a11 2 13 数学上可以写作: a31 032 a33 02 03 其中A为正交矩阵 A = 02 03 a31 032 033 从解析几何知道,符合正交 变换的是:绕固定轴的转动 cos0 -sinθ0 (Rotation about an axis) A= sine 00 绕z轴旋转0角
以上,考察在一定几何变换之下物体的不变性,使 用的几何变换(旋转和反射)都是正交变换——保持 两点距离不变的变换: 11 12 13 21 22 23 31 32 33 ' ' ' x aaa x y aaa y z aaa z ⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎜ ⎟ ⎜ ⎟⎜ ⎟ = ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠⎝ ⎠ i 11 12 13 21 22 23 31 32 33 i j aaa A aaa aaa ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ HG 其中 Aij 为正交矩阵 从解析几何知道,符合正交 变换的是:绕固定轴的转动 (Rotation about an axis) 绕 z 轴旋转 θ 角 cos sin 0 sin cos 0 0 01 Ai j θ θ θ θ ⎛ ⎞ − ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ HG 数学上可以写作:

反演:(Inversion) 1,() A街 x,y,2〉-X,-y,-2 反映(Reflection) m,o (Z=0的平面) 恒等操作 Au 1(E) 0 表示对称操作的符号有两种,这里用的是国际符号
10 0 0 10 00 1 10 0 01 0 00 1 100 010 001 ij ij ij A A A ⎛ ⎞ −⎜ ⎟ = − ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ − ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ − ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ HG HG HG 反演:(Inversion ) 1,(i) 反映 (Reflection ) 恒等操作 m , σ (Z=0 的平面) 1(E) xyz x y z ,, , , →− − − 表示对称操作的符号有两种,这里用的是国际符号
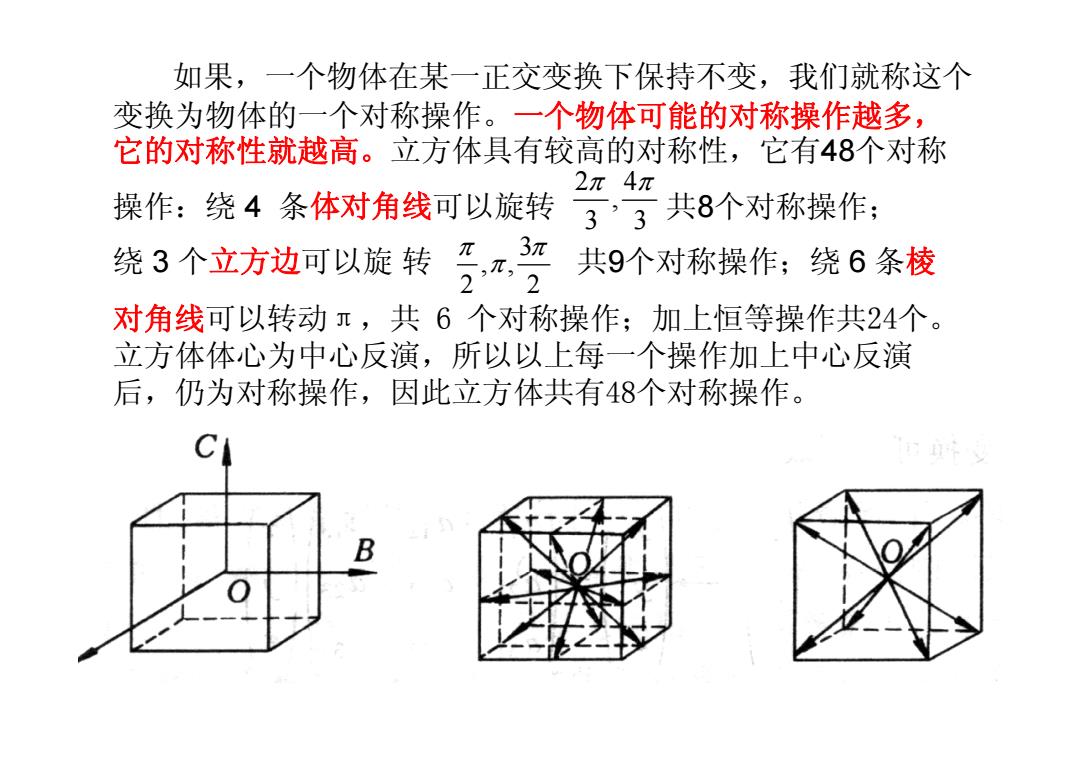
如果,一个物体在某一正交变换下保持不变,我们就称这个 变换为物体的一个对称操作。一个物体可能的对称操作越多, 它的对称性就越高。立方体具有较高的对称性,它有48个对称 2π4π 操作:绕4条体对角线可以旋转 3,3共8个对称操作: 绕3个立方边可以旋转?,,3江 共9个对称操作;绕6条棱 2’2 对角线可以转动兀,共6个对称操作;加上恒等操作共24个。 立方体体心为中心反演,所以以上每一个操作加上中心反演 后,仍为对称操作,因此立方体共有48个对称操作
如果,一个物体在某一正交变换下保持不变,我们就称这个 变换为物体的一个对称操作。一个物体可能的对称操作越多, 它的对称性就越高。立方体具有较高的对称性,它有48个对称 操作:绕 4 条体对角线可以旋转 共 8个对称操作; 绕 3 个立方边可以旋 转 共 9个对称操作;绕 6 条 棱 对角线可以转动π,共 6 个对称操作;加上恒等操作共24个。 立方体体心为中心反演,所以以上每一个操作加上中心反演 后,仍为对称操作,因此立方体共有48个对称操作。 2 4, 3 3 π π 3 , , 2 2 π π π
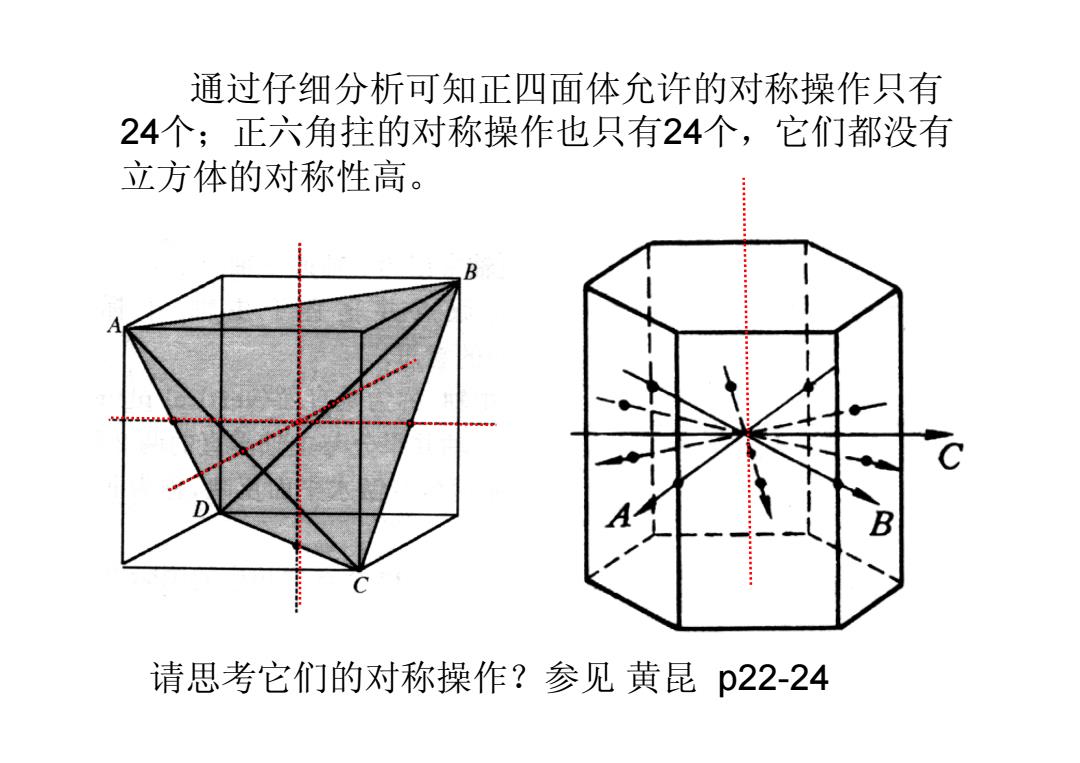
通过仔细分析可知正四面体允许的对称操作只有 24个;正六角拄的对称操作也只有24个,它们都没有 立方体的对称性高。 B 请思考它们的对称操作?参见黄昆p22-24
通过仔细分析可知正四面体允许的对称操作只有 24个;正六角拄的对称操作也只有24个,它们都没有 立方体的对称性高。 请思考它们的对称操作?参见 黄昆 p22-24

对称操作群:一个物体的全部对称操作的集合,构成 对称操作群。描述物体的对称性需要找出物体的全部 对称操作,也就是找出它所具有的对称操作群。 数学上看,群代表一组元素的集合 G={E,A,B,C,D,..} 这些元素被赋予一定的乘法法则,满足下列性质: 1. 若A,B∈G则AB=C∈G,这是群的闭合性。 2.存在单位元素E,使所有元素满足: AE=A 3.任意元素A,存在逆元素:AA-1=E 4. 元素间满足结合律:A(BC)=(AB)C 一个物体全部对称操作的集合,也满足上述群的 定义,运算法则是连续操作,不动操作是单位元素
数学上看,群代表一组元素的集合 G= {E,A,B,C,D, …… } 这些元素被赋予一定的乘法法则,满足下列性质: 1. 若A,B ∈G 则 AB =C ∈ G, 这是群的闭合性。 2. 存在单位元素E,使所有元素满足: AE=A 3. 任意元素 A,存在逆元素:AA-1=E 4. 元素间满足结合律:A(BC)=(AB)C 对称操作群: 一个物体的全部对称操作的集合,构成 对称操作群。描述物体的对称性需要找出物体的全部 对称操作,也就是找出它所具有的对称操作群。 一个物体全部对称操作的集合,也满足上述群的 定义,运算法则是连续操作,不动操作是单位元素

注意:在说明一个物体的对称性时,为了简便,有 时不去一一列举所有的对称操作,而是指出它的对称 元素,若一个物体绕某一个转轴转 2严以及它的倍数 物体保持不变时,便称作n重旋转轴,记做n;若一 个物体绕某一转轴转 2严再作反演以及转动它的倍数 n 再作反演物体保持不变时,该轴称作门重旋转一反演 轴,记做n。立方体的对称元素有:1,2,3,4,i,2,3,4 正四面体的对称元素只有:4,2,3却没有2,4,3 显然,列举出一个物体的对称元素和说出它的对称操 作一样,都可以表明出物体的对称特点
注意: 在说明一个物体的对称性时,为了简便,有 时不去一一列举所有的对称操作,而是指出它的对称 元素,若一个物体绕某一个转轴转 以及它的倍数 物体保持不变时,便称作 n 重旋转轴,记做 n ;若一 个物体绕某一转轴转 再作反演以及转动它的倍数 再作反演物体保持不变时,该轴称作 n 重旋转-反演 轴,记做 。立方体的对称元素有: 正四面体的对称元素只有: 却没有 显然,列举出一个物体的对称元素和说出它的对称操 作一样,都可以表明出物体的对称特点。 2 n π 2 n π n 1,2,3,4, ,2,3,4 i 4,2,3 2,4,3

二.晶体中允许的对称操作: 人们早就指出,晶体的外形(宏观)对称性是其原 子做周期性排列的结果。原子排列的周期性用晶体点阵 表示,晶体本身对称操作后不变,其晶体点阵在对称操 作后也应该保持不变,这就限制了晶体所可能有的点对 称操作数目,可以证明不论任何晶体,它的宏观对称元 素最多只可能有10种(一说8种)对称 元素:1,2,3,4,6,1,2,3,4,6 说明:2是反映面m,而3=3+i,6=3+m 不是独立的。 8种说法指1,2,3,4,6,i,m,4, 对称操作符号,除去以上使用的国际符号外,还通常 使用熊夫利符号
二. 晶体中允许的对称操作: 人们早就指出,晶体的外形(宏观)对称性是其原 子做周期性排列的结果。原子排列的周期性用晶体点阵 表示,晶体本身对称操作后不变,其晶体点阵在对称操 作后也应该保持不变,这就限制了晶体所可能有的点对 称操作数目,可以证明不论任何晶体,它的宏观对称元 素最多只可能有10种(一说8种)对称 元素: 1,2,3,4,6,1,2,3,4,6 说明: 是反映面 m,而 不是独立的。 8种说法指: 对称操作符号,除去以上使用的国际符号外,还通常 使用熊夫利符号。 2 3 3 ,6 3 = + =+ i m 1,2,3,4,6, , ,4, i m