
第一章晶体结构 1.1晶体结构的周期性,晶体点阵 1.2晶体结构的对称性,晶系、点群、空间群 1.3典型晶体结构、晶向、晶面的表示 1.4倒易点阵和布里渊区 1.5晶体结构的实验测定 参考:黄昆、韩汝琦《国体物理学》第一章 Kittel《固体物理导论》一、二章
第一章 晶体结构 1.1 晶体结构的周期性,晶体点阵 1.2 晶体结构的对称性,晶系、点群、空间群 1.3 典型晶体结构、晶向、晶面的表示 1.4 倒易点阵和布里渊区 1.5 晶体结构的实验测定 参考:黄昆、韩汝琦《国体物理学》第 一 章 Kittel 《固体物理导论》一、二 章
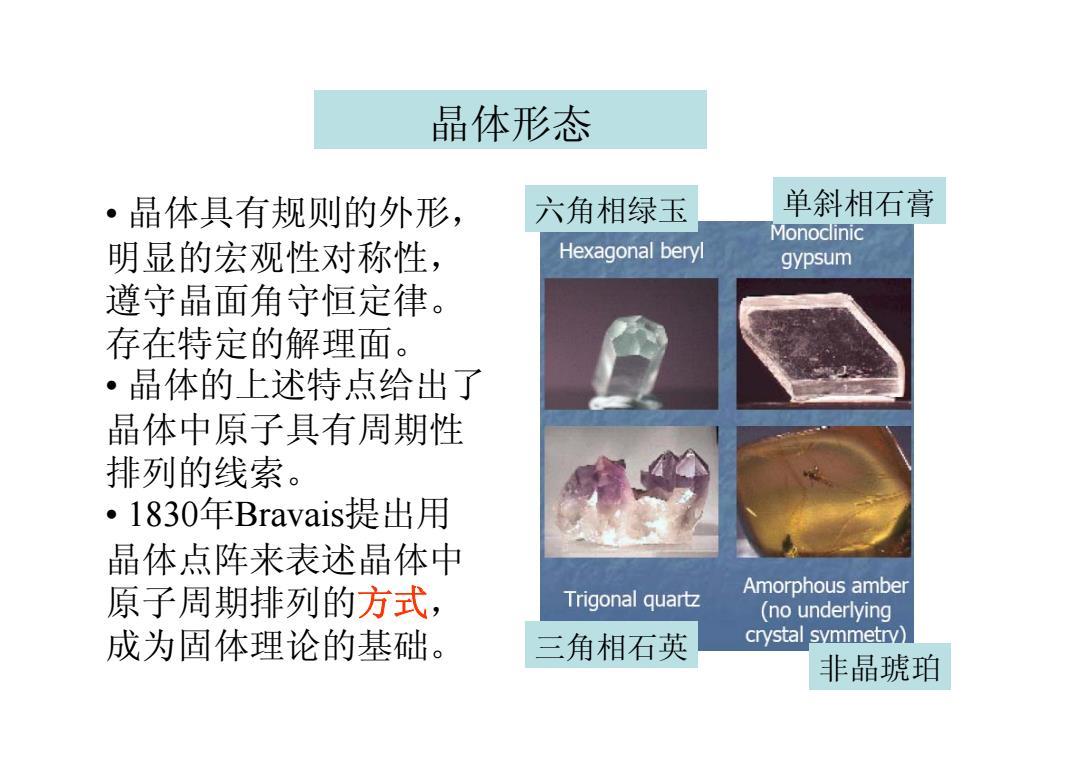
晶体形态 ·晶体具有规则的外形, 六角相绿玉 单斜相石膏 Monodlinic 明显的宏观性对称性, Hexagonal beryl gypsum 遵守晶面角守恒定律。 存在特定的解理面。 ·晶体的上述特点给出了 晶体中原子具有周期性 排列的线索。 ·I830年Bravais提出用 晶体点阵来表述晶体中 原子周期排列的方式, Amorphous amber Trigonal quartz (no underlying 成为固体理论的基础。 三角相石英 crystal symmetry) 非晶琥珀
晶体形态 六角相绿玉 单斜相石膏 三角相石英 非晶琥珀 • 晶体具有规则的外形, 明显的宏观性对称性, 遵守晶面角守恒定律。 存在特定的解理面。 • 晶体的上述特点给出了 晶体中原子具有周期性 排列的线索。 • 1830年Bravais提出用 晶体点阵来表述晶体中 原子周期排列的方式, 成为固体理论的基础
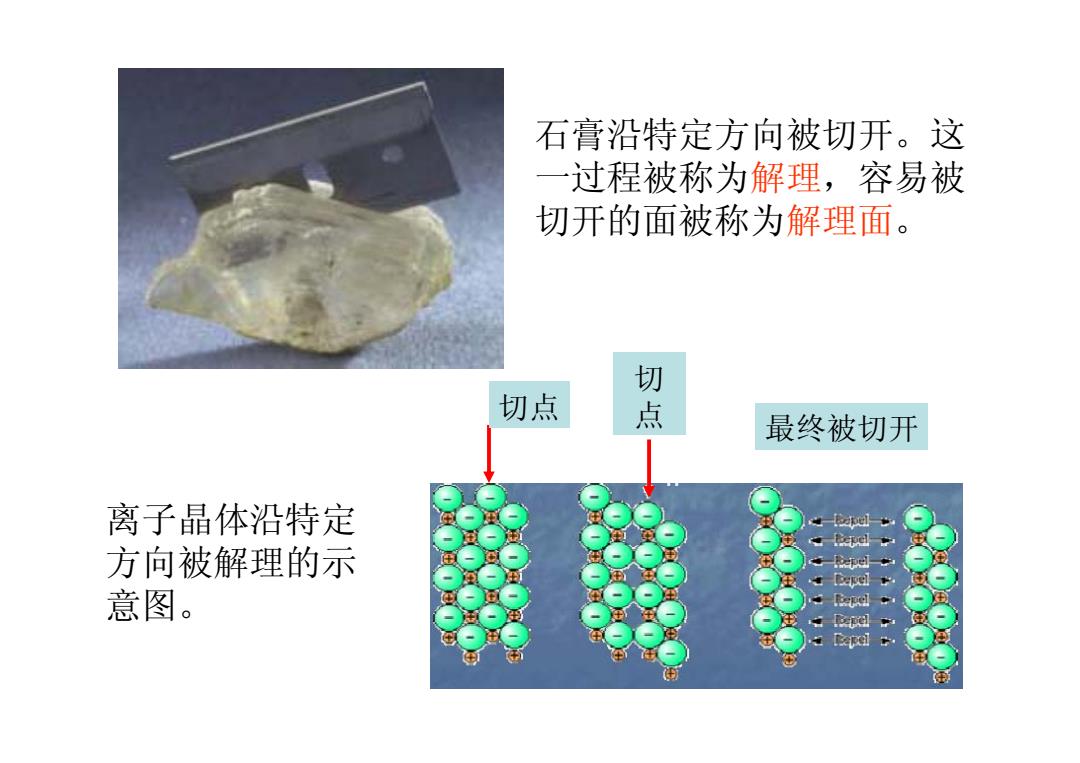
石膏沿特定方向被切开。这 一过程被称为解理,容易被 切开的面被称为解理面。 切 切点 点 最终被切开 离子晶体沿特定 方向被解理的示 意图。 B过 1
切点 切 点 最终被切开 石膏沿特定方向被切开。这 一过程被称为解理,容易被 切开的面被称为解理面。 离子晶体沿特定 方向被解理的示 意图

1.1晶体点阵(Crystal lattice) 一.什么是晶体点阵: X光衍射证实,晶体外形的对称性是其 组成原子在空间做有规律的周期性排列的结 果,为了更好地观察、描述晶体内部原子排 列的方式,我们把晶体中按周期重复排列的 那一部分原子(结构单元)抽象成一个几何 点来表示,忽略重复周期中所包含的具体结 构单元内容而集中反映周期重复方式,这个 从晶体结构中抽象出来几何点的集合称之为 晶体点阵
1.1 晶体点阵(Crystal lattice) 一 . 什么是晶体点阵: X光衍射证实,晶体外形的对称性是其 组成原子在空间做有规律的周期性排列的结 果,为了更好地观察、描述晶体内部原子排 列的方式,我们把晶体中按周期重复排列的 那一部分原子(结构单元)抽象成一个几何 点来表示,忽略重复周期中所包含的具体结 构单元内容而集中反映周期重复方式,这个 从晶体结构中抽象出来几何点的集合称之为 晶体点阵
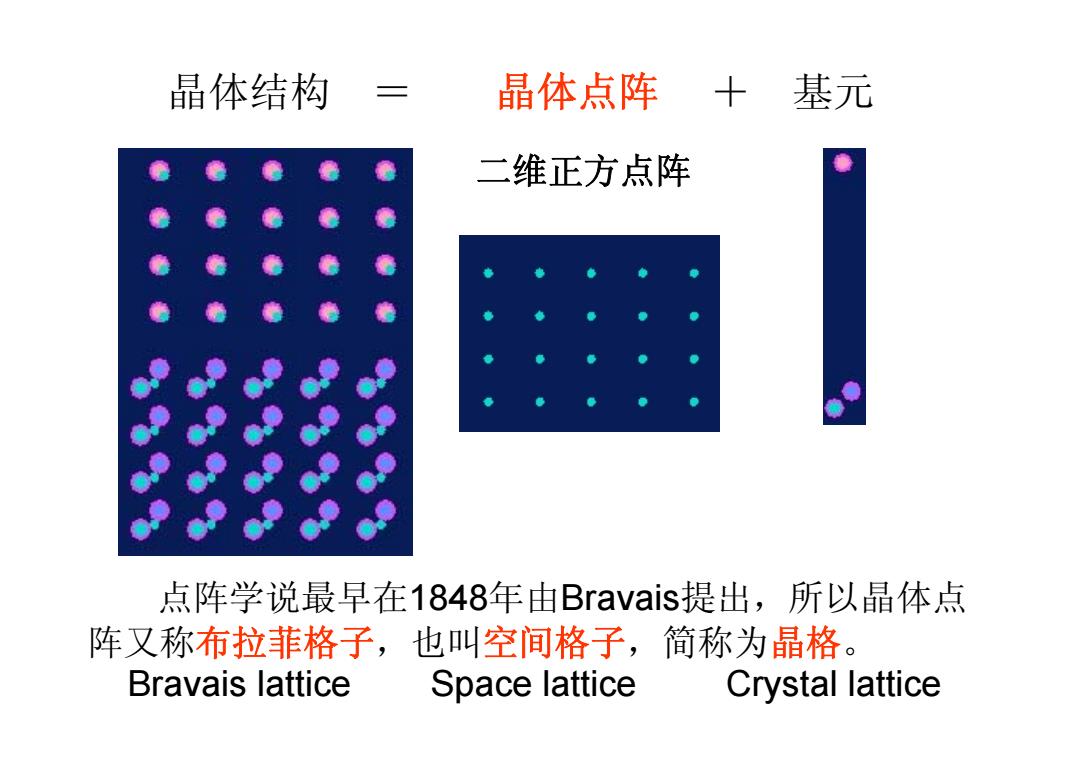
晶体结构 晶体点阵 十基元 二维正方点阵 点阵学说最早在1848年由Bravais提出,所以晶体点 阵又称布拉菲格子,也叫空间格子,简称为晶格。 Bravais lattice Space lattice Crystal lattice
晶体结构 = 晶体点阵 + 基元 二维正方点阵 点阵学说最早在1848年由Bravais提出,所以晶体点 阵又称布拉菲格子,也叫空间格子,简称为晶格。 Bravais lattice Space lattice Crystal lattice

描述晶体表面原子排列的二维长方点阵 (a)空间格点 6)基元,含有两个不同的离子 (⊙)晶体结构
描述晶体表面原子排列的二维长方点阵
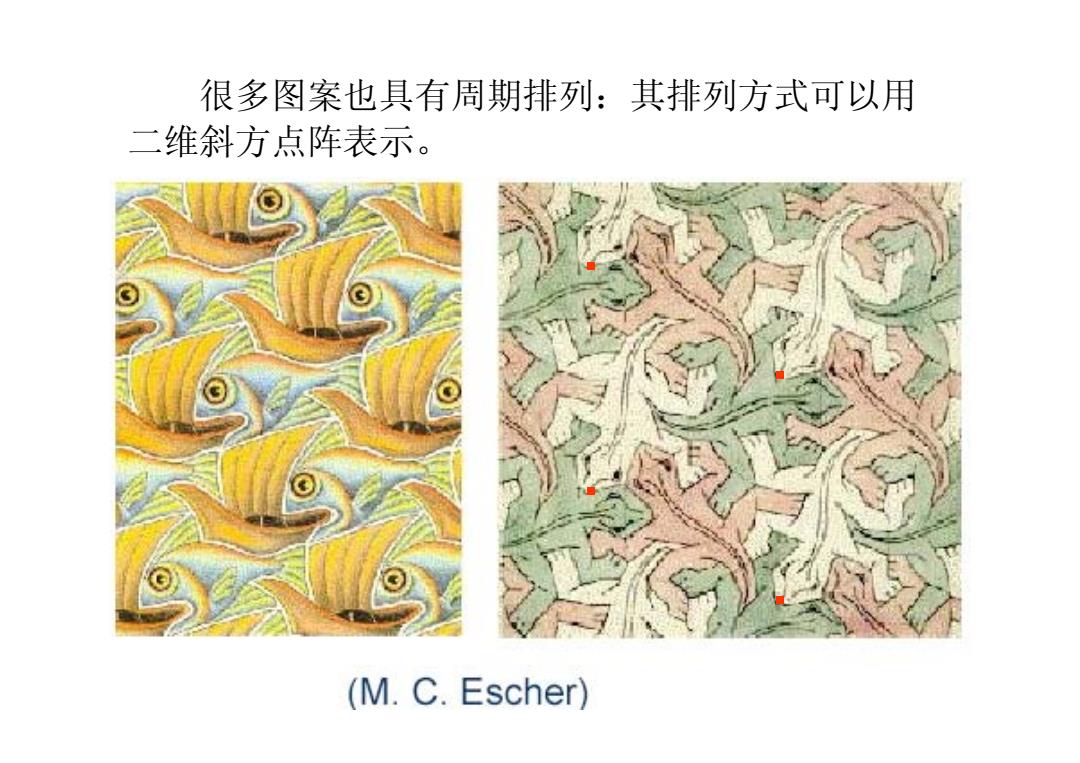
很多图案也具有周期排列:其排列方式可以用 二维斜方点阵表示。 (M.C.Escher)
很多图案也具有周期排列:其排列方式可以用 二维斜方点阵表示。 · · · ·
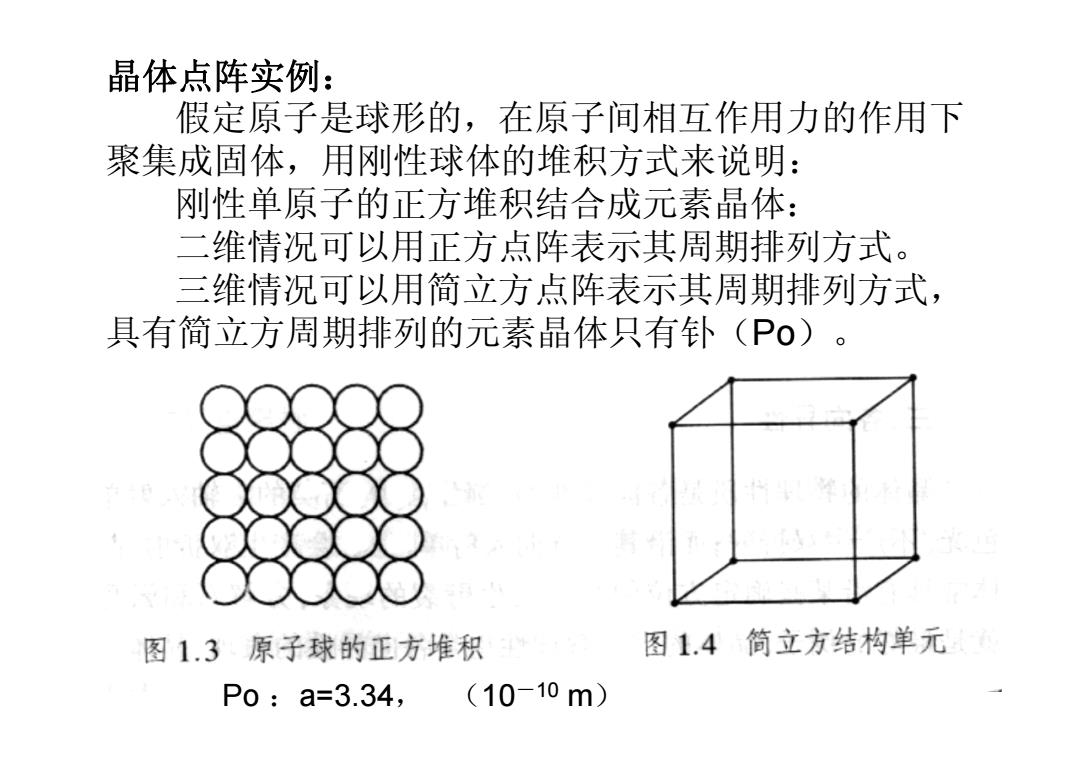
晶体点阵实例: 假定原子是球形的,在原子间相互作用力的作用下 聚集成固体,用刚性球体的堆积方式来说明: 刚性单原子的正方堆积结合成元素晶体: 二维情况可以用正方点阵表示其周期排列方式。 三维情况可以用简立方点阵表示其周期排列方式, 具有简立方周期排列的元素晶体只有钋(Po)。 图1.3原子球的正方堆积 图1.4简立方结构单元 P0:a=3.34,(10-10m)
Po :a=3.34, (10-10 m) 晶体点阵实例: 假定原子是球形的,在原子间相互作用力的作用下 聚集成固体,用刚性球体的堆积方式来说明: 刚性单原子的正方堆积结合成元素晶体: 二维情况可以用正方点阵表示其周期排列方式。 三维情况可以用简立方点阵表示其周期排列方式, 具有简立方周期排列的元素晶体只有钋(Po)

除去元素晶体外,很多化合物晶体的原子也 都具有这种周期排列方式,都可以用简立方点 阵表示。例如:CsC等,只是此时的基元不是 一个原子,而是CsC分子,和CsC晶体相同结 构的化合物还有很多,它们的原子排列方式完 全相同,只是原子之间的距离不同罢了。 CsCl:4.11×1010m;CuZn:2.94×1010m; AINi:2.88 LiHg:3.29 AgMg:3.29 TIBr:3.97
除去元素晶体外,很多化合物晶体的原子也 都具有这种周期排列方式,都可以用简立方点 阵表示。例如:CsCl 等,只是此时的基元不是 一个原子,而是CsCl分子,和CsCl晶体相同结 构的化合物还有很多,它们的原子排列方式完 全相同,只是原子之间的距离不同罢了。 CsCl :4.11 ×10-10 m ; CuZn :2.94 ×10-10 m ; AlNi : 2.88 LiHg :3.29 AgMg :3.29 TlBr : 3.97
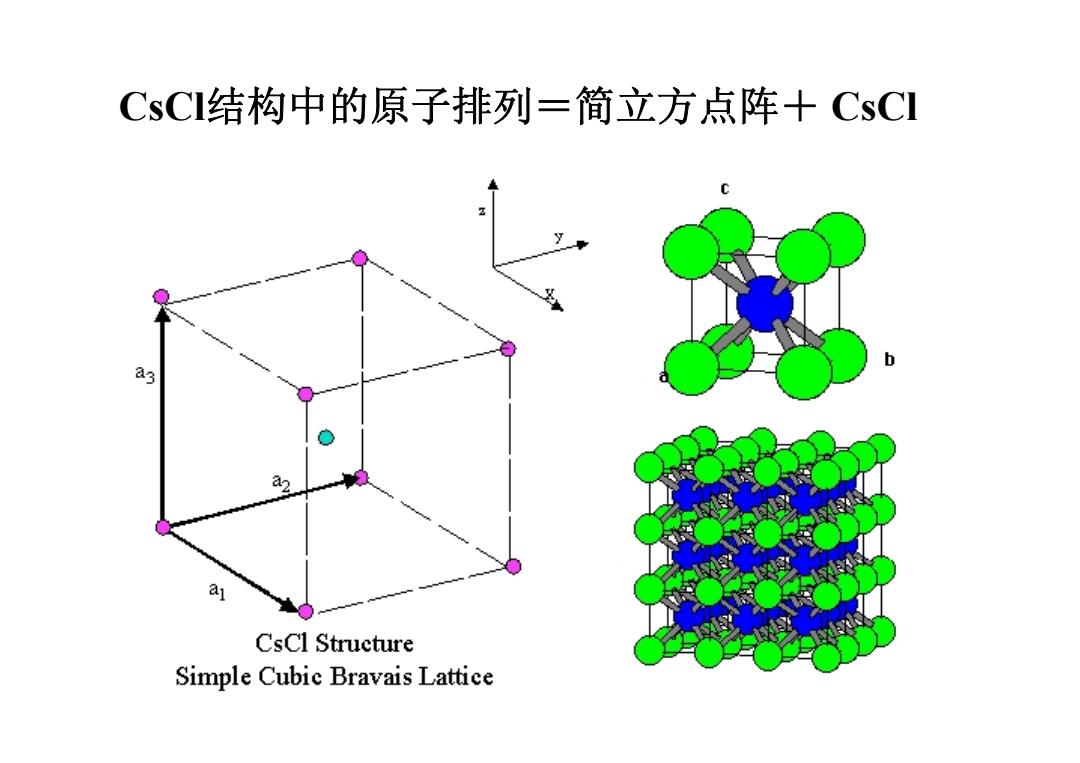
CsCI结构中的原子排列=简立方点阵+CsCI ag a CsCl Structure Simple Cubic Bravais Lattice
CsCl结构中的原子排列=简立方点阵+ CsCl