
4.3金属的热容和顺磁磁化率 一自由电子的热容 二.自由电子的顺磁磁化率 参考:黄昆书p282-286,p395-399 Kittel8版6.4节:11.6节 4.1节中提到:室温下几乎观测不到经典理论预言的自 由电子对热容的贡献,因此索末菲自由电子理论能否正确地 解释金属热容和顺磁磁化率随温度的变化关系,克服经典电 子论的这个困难是它是否成功的考验。 其实从4.2节的描述中已经定性地看到了结果,自由电子 服从费米-狄拉克分布,只有位于费米面附近的少数电子才能 受到kT的热激发,对热容有贡献,其它大部分电子是不能 被激发参与热容贡献的,这就改正了经典理论全部电子都参 与贡献的错误判断
4.3 金属的热容和顺磁磁化率 一. 自由电子的热容 二. 自由电子的顺磁磁化率 参考:黄昆 书p282-286,p395-399 Kittel 8版6.4节;11.6节 4.1 节中提到:室温下几乎观测不到经典理论预言的自 由电子对热容的贡献,因此索末菲自由电子理论能否正确地 解释金属热容和顺磁磁化率随温度的变化关系,克服经典电 子论的这个困难是它是否成功的考验。 其实从4.2节的描述中已经定性地看到了结果,自由电子 服从费米-狄拉克分布,只有位于费米面附近的少数电子才能 受到 kBT 的热激发,对热容有贡献,其它大部分电子是不能 被激发参与热容贡献的,这就改正了经典理论全部电子都参 与贡献的错误判断

一.电子热容量: 4.2中我们曾讨论了T>0K时电子的分布,此时的能量为: (E(E-cEC 仍利用分部积分和函数E)的特点求解,可得: 由于正常情况下E>kT 所以能量随温度的增加很小。 平均到每个电子的能量为: 门
一. 电子热容量: 4.2 中我们曾讨论了T>0K时电子的分布,此时的能量为: ' 3 5 2 2 0 0 0 2 ( ) ( )d ( )d ( )d 5 U Ef E N E E C E f E E CE f E E ¥ ¥ ¥ æ ö = = = ç ÷ è ø ò ò ò 仍利用分部积分和函数 f(E) 的特点求解,可得: 2 2 0 0 5 1 12 B F k T U U E p é ù æ ö = + ê ú ç ÷ ê ú è ø ë û 由于正常情况下 所以能量随温度的增加很小。 0 EF B >> k T 平均到每个电子的能量为: 2 2 2 0 2 0 0 0 5 3 5 1 1 12 5 12 B B F F F k T k T u u E E E p p é ù é ù æ ö æ ö = ê + ú = + ê ú ç ÷ ç ÷ ê è ø ú ê ú è ø ë û ë û

自由电子系统的克分子热容为: C。=N4 - 即便是在较高温度下,T<<TE,所以:Ce<Cy ~1% 但在极低温度下,晶格热容下降很快,电子热容反而会 显著起来。 =bT3 (见3.3节) C。=yT 所以极低温度下,应有: C=C。+Cv=yT+bT3 实验完全证实了这个关系,测出的Y和b值都成了 标识材料性质的量
自由电子系统的克分子热容为: 2 2 0 2 2 B e A A B A B V F F u k T T C N N k N k T E T æ ö ¶ p p æ ö æ ö = ç ÷ = = ç ÷ ç ÷ è ø ¶ è ø è ø 即便是在较高温度下,T<<TF,所以:Ce <<CV。 但在极低温度下,晶格热容下降很快,电子热容反而会 显著起来。 3 12 4 3 5 V A B D T C N k bT T p æ ö = = ç ÷ è ø C T e = g 所以极低温度下,应有: 3 C = Ce V + C = + gT bT 实验完全证实了这个关系,测出的 和 b 值都成了 标识材料性质的量。 g : 1% (见3.3节)
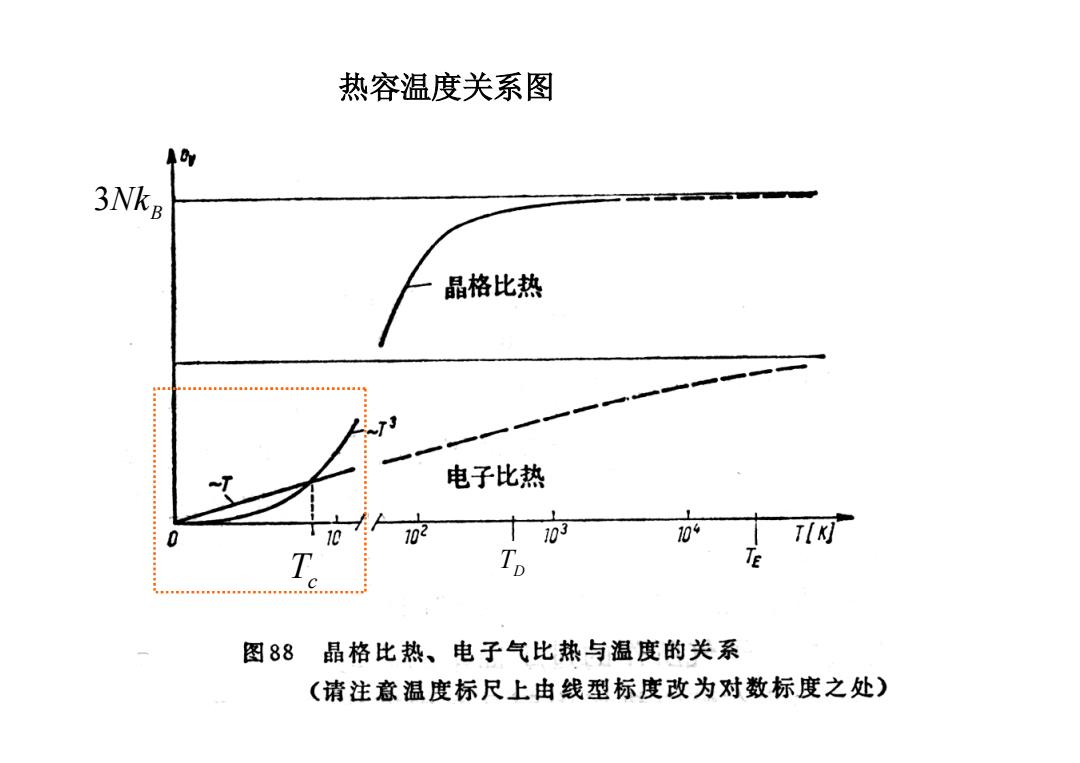
热容温度关系图 3Nkg 晶格比热 电子比热 102 03 10 T[K] T T 图88晶格比热、电子气比热与温度的关系 (请注意温度标尺上由线型标度改为对数标度之处)
热容温度关系图 3NkB TD T c

金属极低温下热容的变化曲线:存在一个临界温度,此温度 以下,电子热容反而变得比 晶格热容更大些。 当Ce=Cv时,有: 号wk (C。+C) 可确定出此时的温度: 1.2 78 4元2TE 对于简单金属,TD~102K, TF~104K,估算出Tc~1K的 数量级。所以,在很低温度 下,电子热容量与晶格热容量 Temperature (kelvins) 同数量级,这时,电子热容量 见:Blakemore书p179 就不可忽略
金属极低温下热容的变化曲线:存在一个临界温度,此温度 以下,电子热容反而变得比 晶格热容更大些。 当Ce=CV时,有: 3 2 12 4 5 2 A B A B D F T T N k N k T T p p æ ö æ ö ç ÷ = ç ÷ è ø è ø 可确定出此时的温度: 3 2 5 24 D c F T T p T = 见:Blakemore 书p179 对于简单金属, TD ~ 102 K, TF ~ 104 K,估算出TC ~ 1 K的 数量级。所以,在很低温度 下,电子热容量与晶格热容量 同数量级,这时,电子热容量 就不可忽略

注意:1.上面的运算过程中,都假定每个原子提供一个自由 电子,如果每个原子提供Z个电子, T T.= 5ZTD 2 T. 24π2TF 2.热容的讨论中,有的文献习惯用克分子热容,有的 则习惯使用单位体积热容,公式形式上是相同的, 只是使用n或NA的差别
2 2 e A B F T C ZN k T p æ ö = ç ÷ è ø 注意:1.上面的运算过程中,都假定每个原子提供一个自由 电子,如果每个原子提供 Z 个电子, 3 2 5 24 D c F ZT T p T = 2. 热容的讨论中,有的文献习惯用克分子热容,有的 则习惯使用单位体积热容,公式形式上是相同的, 只是使用 n 或 NA 的差别
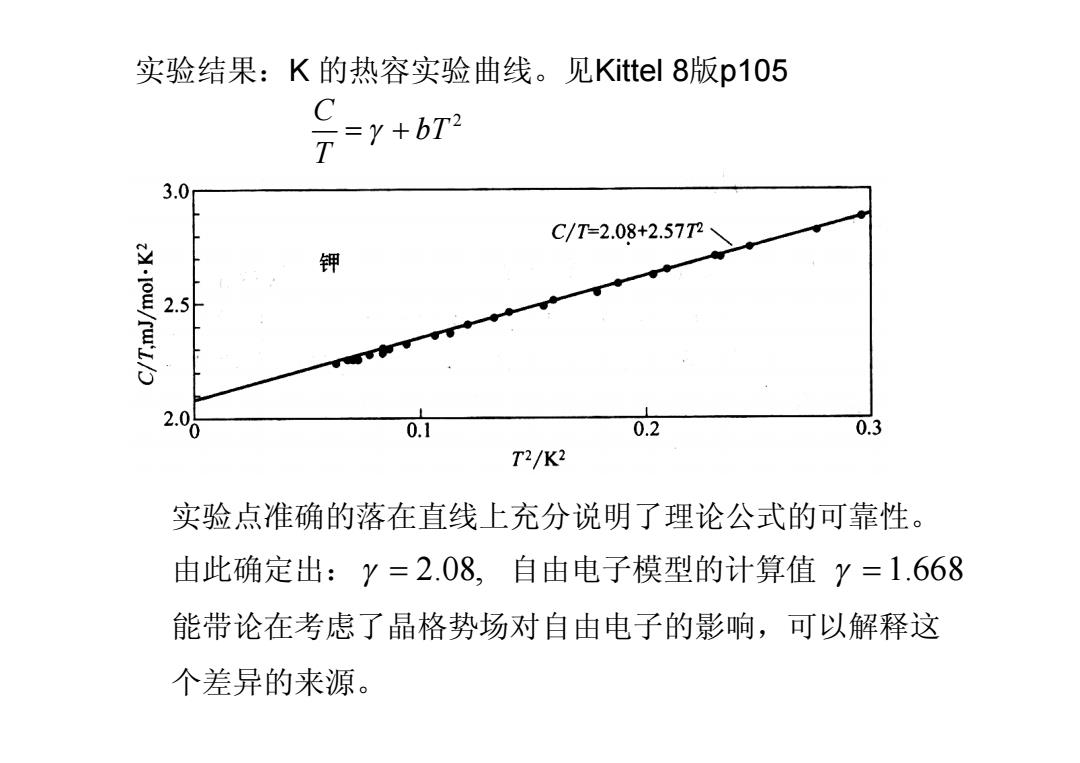
实验结果:K的热容实验曲线。见Kittel8版p105 C =Y+6T2 3.0 C/T=2.08+2.57T2 钾 2.5H 20 0.1 0.2 0.3 T2/K2 实验点准确的落在直线上充分说明了理论公式的可靠性。 由此确定出:y=2.08,自由电子模型的计算值y=1.668 能带论在考虑了晶格势场对自由电子的影响,可以解释这 个差异的来源
实验结果:K 的热容实验曲线。见Kittel 8版p105 C 2 bT T = + g 实验点准确的落在直线上充分说明了理论公式的可靠性。 由此确定出: 自由电子模型的计算值 能带论在考虑了晶格势场对自由电子的影响,可以解释这 个差异的来源。 g = 2.08, g = 1.668

黄昆书p285若干金属的电子热容系数y(mJ/mo1·K)的实验值 Li Be B C N 1.630.11 Na Mg Al Si P 1.381.3 1.35 K Ca Se Ti V Cr Mn(y)Fe Go Ni Cu Zn Ga Ge As 2.082.910.73.359.261.409.204.984.737.020.6950.640.598 0.10 Rb Sr Y Zr Nb Mo Te Ro Rh Pd Ag Cd In Sn()Sb 2.413.610.22.807.792.0-3.34.99.420.6460.6881.691.780.11 Cs Ba La Hf Ta W Re Os Ir Pt Au Hg(a)Tl Pb Bi 3.202.710.02.165.91.32.32.43.16.80.7291.791.472.980.008
黄昆书p285

表2金属中电子比热容常数Y的实验值和基于自由电子的计算值 (引自N.Phillips和N.Pearlman所汇编的资料,热有效质量由式(38)定义), L山 Be B N 1.63 0.17 摘自Kittel8版p105 0749 0.500 2.18 0.34 Na Mg Al Si P 1.38 1.3 y的观测值,mmol.K-2 1.35 1.094 0.992 自曲电了Y的计算值,mJ mol-F.K2 0.912 1.26 1.3 mh/m=(y观测值)/(自由电子y) 1.48 K Ca Sc Ti Cr Mn(Y) Fe Co Ni Cu Zn Ga Ge As 2.08 2.9 10.7 3.35 9.26 1.40 9.20 4.98 4.73 7.02 0.695 0.64 0.596 0.19 1.668 1.511 0.505 0.753 1.025 1.25 1.9 1.38 0.85 0.58 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd n Sn(w) Sb 2.41 3.6 10.2 2.80 7.79 2.0 3.3 4.9 9.42 0.646 0.688 1.69 1.78 0.11 1.911 1.790 0.645 0.948 1.233 1.410 1.26 2.0 1.00 0.73 1.37 1.26 Cs Ba La Hf Ta W Re Os r Pt Au Hg(a) TI Pb Bi 3.20 2.7 10. 2.16 5.9 1.3 2.3 2.4 3.1 6.8 0.729 1.79 1.47 2.98 0.008 2238 1.937 0.642 0952 129 1.509 1.43 14 1.14 1.88 1.14 1.97 系数y的观测值具有所预期的量级,但是同利用关系式(17)和式(34)对质量为m 的自由电子所作的计算结果符合得不甚好。在实际应用中,通常将电子比热容的观测值与自 由电子的比热容值之比表示为热有效质量mt(thermal effective mass)与电子质量n之比, 其中mh由下面关系式定义:
摘自 Kittel 8版p105

从上表中可以看到几个过渡族元素Mn,Fe,Co,Ni具有较 高的电子热容量,从能带论的观点是可以解释的。 通过一定变换, c-号*7)号受[ 可以得到: C= 元2 k2T·N(E) 3 电子热容的实验测量结果也是对费米面附近态密度大小 的反映。所以极低温电子热容的测量成为金属费米面实验研 究的手段之一
从上表中可以看到几个过渡族元素 Mn,Fe,Co,Ni 具有较 高的电子热容量,从能带论的观点是可以解释的。 通过一定变换, 可以得到: 电子热容的实验测量结果也是对费米面附近态密度大小 的反映。所以极低温电子热容的测量成为金属费米面实验研 究的手段之一。 2 2 0 ( ) 3 Ce B F k T N E p = × 2 2 2 2 2 0 0 2 2 2 A e A B A F F F F F T T N C N k N k k T T E E p æ ö p p æ ö æ ö = ç ÷ = = ç ÷ ç ÷ è ø è ø è ø