
1.4倒易点阵和布里渊区 (Reciprocal lattice;Brillouin zones) 一.定义 二.倒易点阵和晶体点阵的关系 三.倒易点阵的物理意义 四.倒易点阵实例 五.布里渊区 参考:黄昆书1.3节;p175-179;Kittel8版2.3节
1.4 倒易点阵和布里渊区 (Reciprocal lattice; Brillouin zones) 一 . 定义 二. 倒易点阵和晶体点阵的关系 三. 倒易点阵的物理意义 四. 倒易点阵实例 五. 布里渊区 参考:黄昆书 1.3 节;p175-179; Kittel 8版 2.3 节

一.定义:假设1,a2,a3是一个晶体点阵的基矢,该点阵的 格矢为:Rm=n,a+n,a2+na3 原胞体积是: 2=a1(a2×a3) 现在定义3个新的基矢 b1=2π a2×a3 a1·(a2xa3) 1,b2,b3构成一个新点阵: b2=2π a3×a1 a·(a2×ā) (h,k,I是整数。) b=2π a1×a2 a(a2×a3 位移矢量 Gnkl hbr+kb2+1b3 就构成了上面点阵的 倒易点阵,上面变换公式中出现的2π因子,对于晶体学 家来说并没有多大用处,但对于固体物理研究却带来了极 大的方便。倒易点阵的概念是Ewald1921年在处理晶体X 射线衍射问题时首先引入的,对我们理解衍射问题极有帮 助,更是整个固体物理的核心概念
一 . 定义:假设 是一个晶体点阵的基矢,该点阵的 格矢为: 原胞体积是: 现在定义 3个新的基矢 构成一个新点阵: ( ) ( ) ( ) 1 2 3 1 2 3 1 2 3 3 1 2 1 2 3 2 3 1 2 2 2 a a a a a b a a a a a b a a a a a b K K K K K K K K K K K K K K K K K K ⋅ × × = ⋅ × × = ⋅ × × = π π π 位移矢量 就构成了上面点阵的 倒易点阵,上面变换公式中出现的 因子,对于晶体学 家来说并没有多大用处,但对于固体物理研究却带来了极 大的方便。倒易点阵的概念是Ewald 1921年在处理晶体X 射线衍射问题时首先引入的,对我们理解衍射问题极有帮 助,更是整个固体物理的核心概念。 aaa 123 , , G G G Ω= × aa a 12 3 ( ) G G G Rn =++ na na na 11 1 123 i JG G G G bbb 123 , , GGG 2π G hb kb lb hkl =++ 1 23 JG G G G ( h,k,l 是整数。)

二.倒易点阵和晶体点阵之间的关系: 倒易点阵是从晶体点阵(以后简称正点阵)中定义出的, 可以方便地证明它和正点阵之间有如下关系: b,·d,=2πδ 1.两个点阵的基矢之间: 1,i=j 0,i≠ 1 2.两个点阵的格矢之积是2π的整数倍: Gh.Rn=2πm 3.两个点阵原胞体积之间的关系是: 2°=b1(b2xb3)= (2π)3 2 4.正点阵晶面族(h,k,I)与倒易点阵格矢Gk相互垂直, Gnkl hb1 +kb2 +163 且有: 2π d
二. 倒易点阵和晶体点阵之间的关系: 倒易点阵是从晶体点阵(以后简称正点阵)中定义出的, 可以方便地证明它和正点阵之间有如下关系: 2. 两个点阵的格矢之积是 的整数倍: 3. 两个点阵原胞体积之间的关系是: 4. 正点阵晶面族 与倒易点阵格矢 相互垂直, 1. 两个点阵的基矢之间: 2π ( ,k,l) h Ghkl JG Ghkl 1 2 3 =++ hb kb lb JG G G G 且有: ⎩⎨⎧ ≠= = ⋅ = i j i j b a ij i j ij 0 , 1, 2 δ πδ K K G R h n = 2 mπ JG JG i 3 * 12 3 (2 ) bb b ( ) π Ω= × = Ω G G G i 2 hkl hkl d G π = JG

1.证明:根据矢量运算规则,从倒格矢定义即可说明。 2.证明: Rn-Gm (nar+na2+na3)(hb+kb2 +1b3) =2π(n,h+n,k+n)=2πm (m为整数) 4.证明:先证明倒格矢Gh4=h,a1+ha2+h,a3 与正格子的晶面系(h,hh3)正交。 如图所示,晶面系(h,h,h)中最靠近原点的晶面(ABC) 在正格子基矢a1,a2,a3的截距分别为:a1a2a3 h’h2’h
2. 证明: 1 2 3 1 23 11 1 123 ( )( ) 2( ) 2 R G n a n a n a hb kb lb n hkl π π nh nk nl m = + + ++ = ++ = JG JG G G G G G G i i (m 为整数) 1. 证明:根据矢量运算规则,从倒格矢定义即可说明。 4. 证明:先证明倒格矢 与正格子的晶面系 正交。 如图所示,晶面系 中最靠近原点的晶面(ABC) 在正格子基矢 的截距分别为: 123 ,, 1 2 3 12 3 G ha ha ha hh h =+ + JG GGG 123 ( ) hhh 123 ( ) hhh aaa 123 , , G G G 123 123 , , aaa hhh G G G
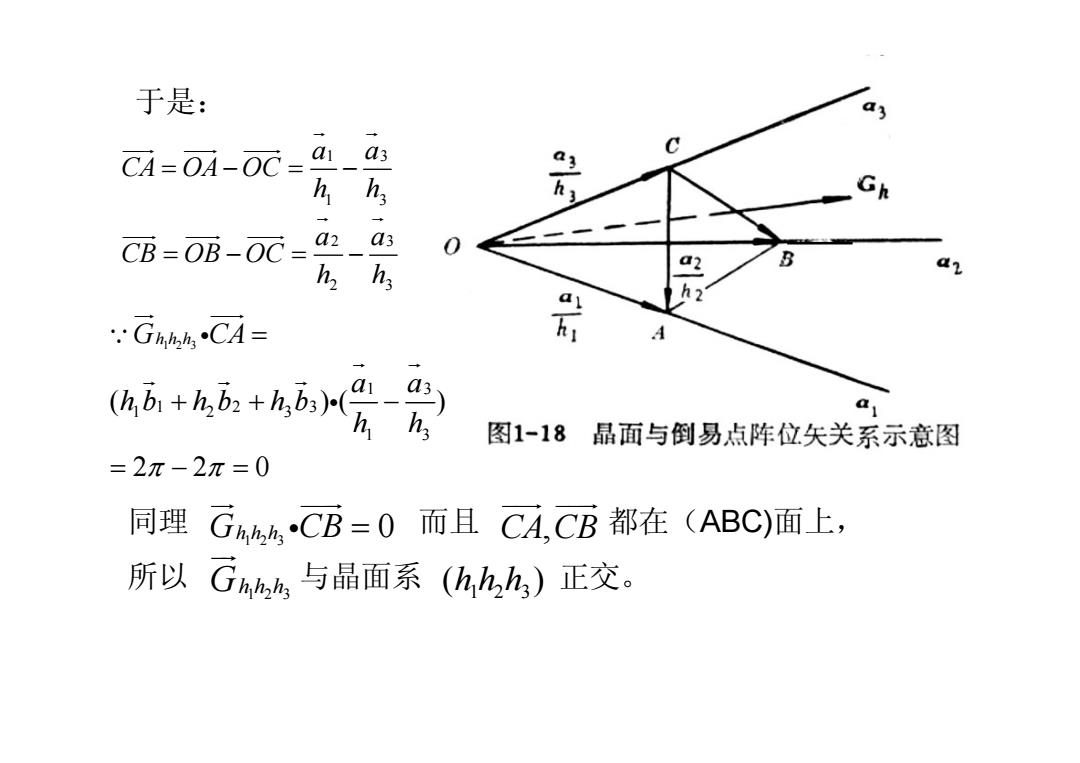
于是: CA=OA-OC as Gh CB=0B-OC= a3 0 h h a2 az h2 ·G4h4CA= A A6+hb+Ab爱爱 图1-18 晶面与倒易点阵位矢关系示意图 =2π-2π=0 同理 Gh,CB=0而且CA,CB都在(ABC)面上, 所以 Gh,与晶面系(h,h,h)正交
1 3 1 3 2 3 2 3 a a CA OA OC h h a a CB OB OC h h = − =− = − =− G G JJG JJJG JJJG G G JJJG JJJG JJJG 于是: 123 1 3 123 12 3 1 3 ( )( ) 220 G CA hh h a a hb hb hb h h π π = ++ − =−= JG JJG ∵ i G G GGG i G CB hh h 123 = 0 JG JJJG 同理 而且 都在( i ABC)面上, 所以 与晶面系 正交。 CA CB , JJG JJJG 123 Ghh h JG 123 ( ) hhh

晶面系的面间距就是原点到ABC面的距离,由于Gh,⊥(ABC) 可以证明: =OA 2π dahnls G Giah 由此我们得出结论:倒易点阵的一个基矢是和正点阵晶格中 的一族晶面相对应的,它的方向是该族晶面的法线方向,而 它的大小是该族晶面面间距倒数的2π倍。又因为倒易点阵基 矢对应一个阵点,因而可以说:晶体点阵中的晶面取向和晶 面面间距这2个参量在倒易点阵里只用一个点阵矢量(或说 阵点)就能综合地表达出来
晶面系的面间距就是原点到ABC面的距离,由于 可以证明: 123 G ABC hh h ⊥ ( ) JG 123 123 123 123 hh h 2 hh h hh h hh h G d OA G G π = = JG JJJG i JG JG 由此我们得出结论:倒易点阵的一个基矢是和正点阵晶格中 的一族晶面相对应的,它的方向是该族晶面的法线方向,而 它的大小是该族晶面面间距倒数的 2π倍。又因为倒易点阵基 矢对应一个阵点,因而可以说:晶体点阵中的晶面取向和晶 面面间距这 2 个参量在倒易点阵里只用一个点阵矢量(或说 阵点)就能综合地表达出来
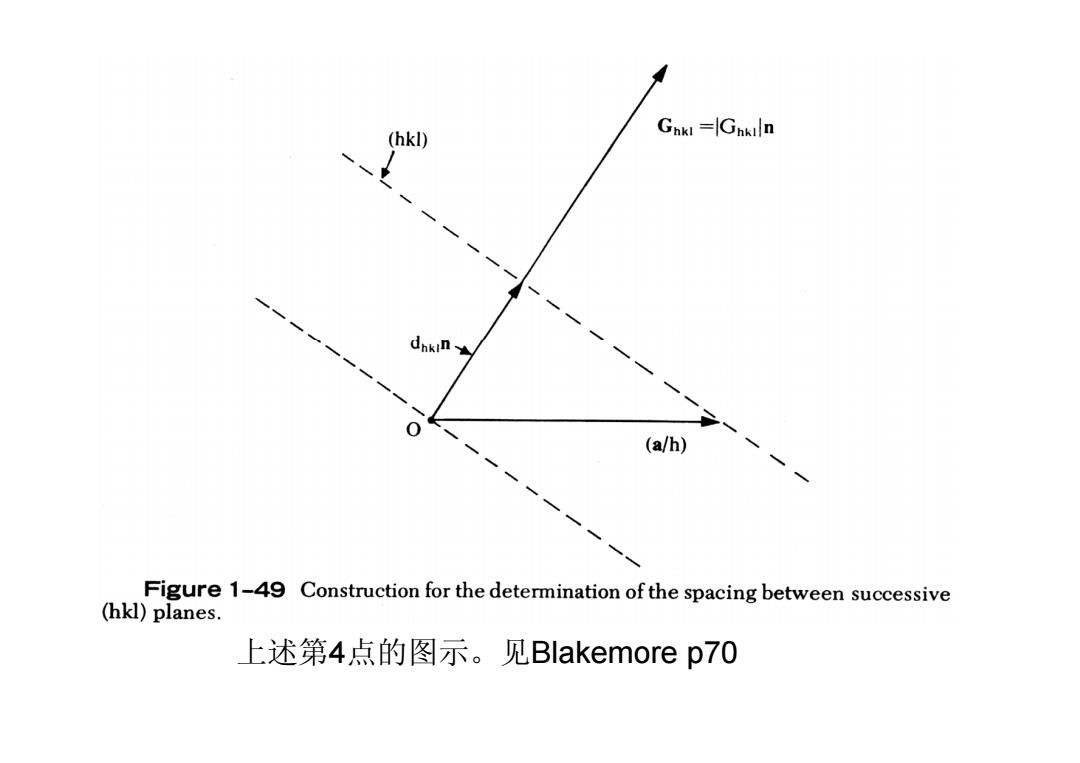
(hkl) Gnkl =Ghkiln 0 (a/h) Figure 1-49 Construction for the determination of the spacing between successive (hkl)planes. 上述第4点的图示。见Blakemore p70
上述第4点的图示。见Blakemore p70

5.正点阵和倒易点阵是互易的:由正点阵a,a2,a3给出倒易 点阵b1,b2,3现假定b1,b2,b为正点阵,则其 倒易点阵根据定义:一c,=2元(2×) 利用三重矢积公式:Ax(BxC)=B(AC)-C(AB) 可以得到不×系-晋aa日aa)-2a Ω 又因为: 2.2=b1(b2×b3)2=(2π)2(a1b1)=(2π) 所以: 0- 2π(2π)2-- a1=a1 Ω Ω 同样可以证明:C2=a2,C3=Q3
5. 正点阵和倒易点阵是互易的:由正点阵 给出倒易 点阵 现假定 为正点阵,则其 倒易点阵根据定义为: bbb 123 , , G G G 2 3 1 * 2 c bb ( ) π = × Ω G G 2 23 31 12 1 2 2 (2 ) bb aa aa a ( )( ) ππ π ×= × × × = ΩΩ Ω G G GG GG G A×× = − ( )( )( ) B C B AC C AB JG JG JG JG JG JG JG JG JG 利用三重矢积公式: i i 可以得到: * 23 Ω ⋅Ω = × ⋅Ω = = b b b ab 1 2 3 11 ( ) (2 ) ( ) (2 ) π π G G G GG i i 2 1 11 * 2 (2 ) c aa π π = = Ω Ω G G G 又因为: 所以: c ac a 2 23 3 = = , , G GG G 同样可以证明: bbb 123 , , GGG aaa 123 , , G G G

三.倒易点阵(Reciprocal lattice)的物理意义: 倒易点阵的物理意义和在分析周期性结构和相应物性中 作为基本工具的作用,需要我们在使用中逐步理解。 当一个点阵具有位移矢量Rm=n,a1+n,a2+na3 时,考虑到周期性特点,一个物理量在r点的数值「() 也应该具有周期性:『(r)=T(r+R) 两边做Fourier展开,有: >I(G)exp(iG)=>I(G)exp(iG)exp(iGw-R.) 显然: exp(iGnkI-Rn)=1, 即: G-Rn=2πm 既然R是正点阵的格矢,符合该关系的 Ghkt 就是倒易点阵 的格矢。所以,同一物理量在正点阵中的表述和在倒易点阵中 的表述之间服从Fourier变换关系
三. 倒易点阵(Reciprocal lattice)的物理意义: 倒易点阵的物理意义和在分析周期性结构和相应物性中 作为基本工具的作用,需要我们在使用中逐步理解。 当一个点阵具有位移矢量 时,考虑到周期性特点,一个物理量在 r 点的数值 也应该具有周期性: 两边做Fourier展开,有: 显然: 即: 123 11 1 Rn =++ na na na JG GGG Γ( )r Γ =Γ + () ( ) r rRn G G JG ( ) exp( ) ( ) exp( ) exp( ) hkl hkl hkl hkl hkl n K K ∑ ∑ Γ =Γ G iG r G iG r iG R JG JG G JG JG G JG JG i ii exp( ) 1, 2 m hkl n hkl n iG R G R π = = JG JG i JG JG i 既然 是正点阵的格矢,符合该关系的 就是倒易点阵 的格矢。所以,同一物理量在正点阵中的表述和在倒易点阵中 的表述之间服从Fourier变换关系。 Rn JG Ghkl JG

实际上,晶体结构本身就是一个具有晶格周期性的 物理量,所以也可以说:倒易点阵是晶体点阵的 Fourier?变换,晶体点阵则是倒易点阵的Fourier逆变换。 因此,正格子的量纲是长度1,称作坐标空间,倒格子 的量钢是长度的倒数卜1,称作波矢空间。例如:正点阵 取cm,倒易点阵是cm-1,下面我们将看到: 晶体的显微图像是真实晶体结构在坐标空间的映像。 晶体的衍射图像则是晶体倒易点阵的映像。 倒易点阵是在晶体点阵(布拉菲格子)的基础上定 义的,所以每一种晶体结构,都有2个点阵与其相联 系,一个是晶体点阵,反映了构成原子在三维空间做周 期排列的图像;另一个是倒易点阵,反映了周期结构物 理性质的基本特征
实际上,晶体结构本身就是一个具有晶格周期性的 物理量,所以也可以说:倒易点阵是晶体点阵的 Fourier变换,晶体点阵则是倒易点阵的Fourier逆变换。 因此,正格子的量纲是长度 l, 称作坐标空间,倒格子 的量钢是长度的倒数 l-1,称作波矢空间。例如:正点阵 取cm,倒易点阵是cm-1, 下面我们将看到: 晶体的显微图像是真实晶体结构在坐标空间的映像。 晶体的衍射图像则是晶体倒易点阵的映像。 倒易点阵是在晶体点阵(布拉菲格子)的基础上定 义的,所以每一种晶体结构,都有 2个点阵与其相联 系,一个是晶体点阵,反映了构成原子在三维空间做周 期排列的图像;另一个是倒易点阵,反映了周期结构物 理性质的基本特征