
6.1晶体中电子的运动特征: Bloch电子的准经典描述 二.波包与电子速度 三.电子的准动量 四.电子的加速度和有效质量 见黄昆书5.1节p237 在我们给出了电子在晶体周期势场中运动的本征态和 本征能量之后,就可以开始研究晶体中电子运动的具体问 题了,由于周期势场的作用,晶体中的电子的本征能量和 本征函数都已不同于自由电子,因而在外场中的行为也完 全不同于自由电子,我们称之为Bloch电子。首先分析一 下它和自由电子的区别及其一般特征
6.1 晶体中电子的运动特征: 在我们给出了电子在晶体周期势场中运动的本征态和 本征能量之后,就可以开始研究晶体中电子运动的具体问 题了,由于周期势场的作用,晶体中的电子的本征能量和 本征函数都已不同于自由电子,因而在外场中的行为也完 全不同于自由电子,我们称之为 Bloch 电子。首先分析一 下它和自由电子的区别及其一般特征。 一. Bloch 电子的准经典描述 二. 波包与电子速度 三. 电子的准动量 四. 电子的加速度和有效质量 见黄昆书5.1节p237

一.Bloch电子的准经典描述: 当外加场(电场、磁场等)施加到晶体上时,晶体中 的电子不只是感受到外场的作用,而且还同时感受着晶体 周期场的作用。通常情况下,外场要比晶体周期势场弱得 多。因为晶体周期场强度一般相当于108Vcm。而外电场 是难以达到这个强度的。因此,晶体中的电子在外场中的 运动必须在周期场本征态的基础上进行讨论。采用的方法 有两种: ◆求解含外场的单电子波动方程。 ◆ 或者是在一定条件下,把晶体中电子在外场中的运动 当作准经典粒子来处理。 注解:例如氢原子的基态能(电离能)为13.6eV
一. Bloch 电子的准经典描述: 当外加场(电场、磁场等)施加到晶体上时,晶体中 的电子不只是感受到外场的作用,而且还同时感受着晶体 周期场的作用。通常情况下,外场要比晶体周期势场弱得 多。因为晶体周期场强度一般相当于 108 V/cm。而外电场 是难以达到这个强度的。因此,晶体中的电子在外场中的 运动必须在周期场本征态的基础上进行讨论。采用的方法 有两种: u 求解含外场的单电子波动方程。 u 或者是在一定条件下,把晶体中电子在外场中的运动 当作准经典粒子来处理。 注解:例如氢原子的基态能(电离能)为 13.6 eV

含外场的波动方程 [r+0rv-m 通常情况下求解含外场的波动方程,但只能近似求解。 另一种方法是在: 外场较弱且恒定。 不考虑电子在不同能带间的跃迁。 不考虑电子的衍射、干涉及碰撞。 等条件下把晶体中电子在外场中的运动当作准经典粒子 来处理。这种方法图像清晰,运算简单,我们乐于采用
通常情况下求解含外场的波动方程,但只能近似求解。 ( ) 2 2 2 U V E m y y é ù - Ñ + + = ê ú ë û h r 含外场的波动方程 外场较弱且恒定。 不考虑电子在不同能带间的跃迁。 不考虑电子的衍射、干涉及碰撞。 另一种方法是在: 等条件下把晶体中电子在外场中的运动当作准经典粒子 来处理。这种方法图像清晰,运算简单,我们乐于采用

经典粒子同时具有确定的能量和动量,但服从量子力学 运动规律的微观粒子是不可能的,如果一个量子态的经典描 述近似成立,则在量子力学中这个态就要用一个“波包”来代 表,所谓波包是指该粒子(例如电子)空间分布在“,附近的 △r范围内,动量取值在k,附近的△k范围内,△r△k满 足测不准关系。把波包中心r。看作该粒子的位置,把k。看 作该粒子的动量。 晶体中的电子,可以用其本征函数Bloch波组成波包, 从而当作准经典粒子来处理
经典粒子同时具有确定的能量和动量,但服从量子力学 运动规律的微观粒子是不可能的,如果一个量子态的经典描 述近似成立,则在量子力学中这个态就要用一个“波包”来代 表,所谓波包是指该粒子(例如电子)空间分布在 r0 附近的 △r 范围内,动量取值在 附近的 范围内, 满 足测不准关系。把波包中心 r0 看作该粒子的位置,把 看 作该粒子的动量。 晶体中的电子,可以用其本征函数 Bloch波组成波包, 从而当作准经典粒子来处理。 0 hk hDk D Dr k 0 hk

二.波包与电子速度: 在晶体中,电子的准经典运动可以用Bloch函 数组成的波包描述。由于波包中含有能量不同的本 征态,因此,必须用含时间因子的Bloch函数。 首先考虑于一维情况。设波包由以k为中心, 在△k的范围内的波函数组成,并假设△k很小,可 近似认为 4,(x)≈4(x) 不随k而变。 对于一确定的k,含时间的Bloch函数为 w(x,)=e-ol4,(x) (k)=E(k)/h 把与k,相邻近的各k'状态叠加起来就可以组成 与量子态k,相对应的波包:
二. 波包与电子速度: 在晶体中,电子的准经典运动可以用 Bloch 函 数组成的波包描述。由于波包中含有能量不同的本 征态,因此,必须用含时间因子的Bloch 函数。 首先考虑于一维情况。设波包由以 k0为中心, 在 Dk 的范围内的波函数组成,并假设 Dk 很小,可 近似认为 ( ) ( ) 0 k k u x » u x 不随 k 而变。 对于一确定的 k ,含时间的Bloch函数为 ( ) ( ) , ( ) i kx t k k x t e u x w y - = w (k ) = E k( )/ h 把与 k0 相邻近的各 k’ 状态叠加起来就可以组成 与量子态 k0 相对应的波包:

tu平(x.-e-u()iko0间 4(小eak 令为=k+5e0@服 e0-aaa四-l =4(x)ek 2sin{[x-(架)人] x-(架)
波包 ( ) ( ) ( ) 0 2 0 2 , d k k k i kx t k k x t e u x k w D D + - - Y = ò ( ) ( ) 0 2 0 0 2 d k k k i kx t k k u x e k w D D + - - » ò 令 0 k k = + x ( ) 0 0 d d k k k w w w x æ ö » + ç ÷ è ø ( ) ( ) ( ) 0 0 0 0 2 2 d , exp d d k k i k x t k k x t u x e i x t k w w x x D D - - ì ü ï ï é ù æ ö Y = - í ý ê ú ç ÷ ï ï ê ú è ø î þ ë û ò ( ) ( ) { ( ) } ( ) 0 0 0 0 0 2 2sin k i k x t k k k d dk d dk x t u x e x t w w w - D é ù - ë û = × - ( ) ( ) 0 k k u x » u x
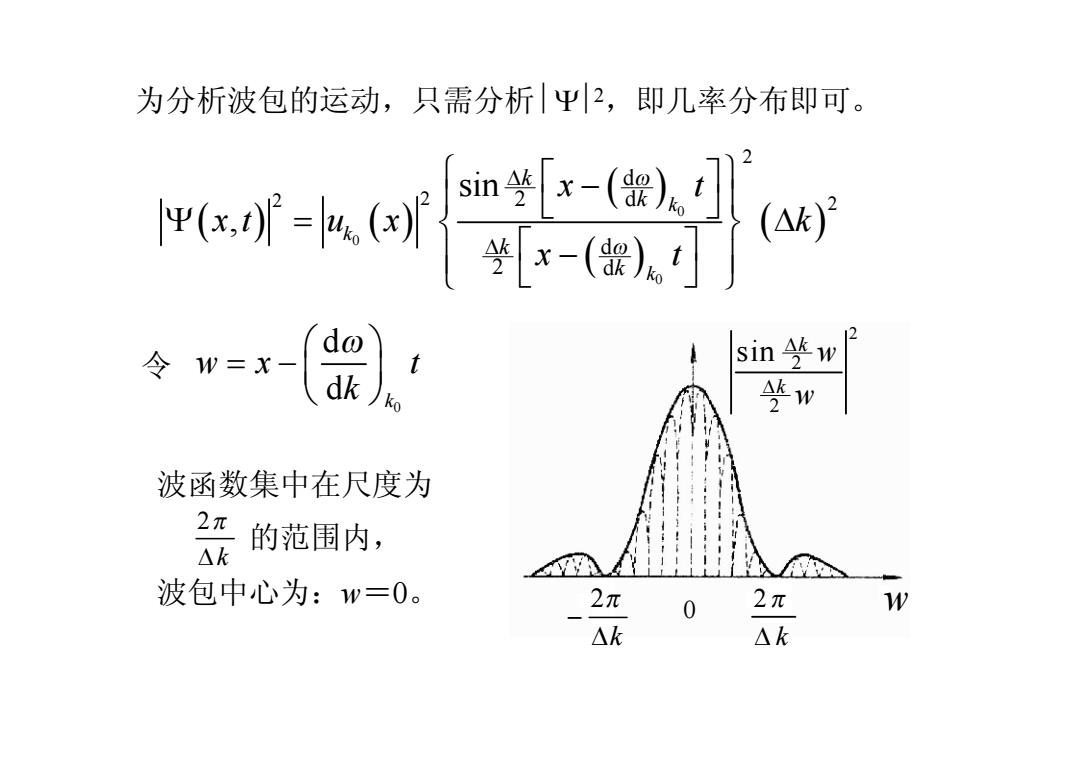
为分析波包的运动,只需分析平2,即几率分布即可。 (w) sinw 竖w 波函数集中在尺度为 2 的范围内, △k 波包中心为:w=0。 2兀 0 2π W △K △k
为分析波包的运动,只需分析 êYï2 ,即几率分布即可。 ( ) ( ) ( ) ( ) ( ) 0 0 0 2 2 2 2 d 2 d d 2 d sin , k k k k k k k x t x t u x k x t w w D D ì ü é ù - ï ï ë û Y = D í ý ï ï é ù - î þ ë û 令 0 d d k w x t k æ ö w = - ç ÷ è ø 2 w k p D 2 k p - D 0 2 2 2 sin k k w w D D 波函数集中在尺度为 的范围内, 波包中心为:w=0。 2 k p D

do 有 x= dk )ko dk )ko E(k)=ho(k) 若将波包看成一个准粒子,则粒子的速度为 ) 布里渊区的宽度:2π/,而假设△k很小,一般要求 .2π 即 2元 △k>a a △k 推广到三维情况,电子速度为 V= VE 抗
有 0 0 d 1 d d d k k E x t t k k æ w ö æ ö = = ç ÷ ç ÷ è ø h è ø 若将波包看成一个准粒子,则粒子的速度为 ( ) 0 0 d 1 d d d k x E v k t k æ ö = = ç ÷ h è ø E(k k ) = hw ( ) 布里渊区的宽度:2p/a ,而假设 Dk 很小,一般要求 即 推广到三维情况,电子速度为 1 = Ñ E h k v a k 2p D > D 2p

注意,这里给出了把B引och波当作准经典粒子处理的条件。 由于B引och波有色散,一个稳定的波包所包含的波矢范围△k 应是一个很小的量。B引och波有独立物理意义的波矢被限制 在第一布里渊区内,△k>a 这表明,如果波包的大小比原胞尺寸大得多,晶体中电子的 运动就可以用波包的运动规律来描述。对于输运现象,只有 当电子平均自由程远大于原胞尺寸的情况下,才可以把晶体 中的电子当作准经典粒子,波包移动的速度(群速度)等于 处于波包中心处粒子所具有的平均速度
注意,这里给出了把 Bloch 波当作准经典粒子处理的条件。 由于Bloch 波有色散,一个稳定的波包所包含的波矢范围△k 应是一个很小的量。Bloch 波有独立物理意义的波矢被限制 在第一布里渊区内, 因为测不准关系 2 x x Dp ×Dx = Dk x ×D ³ h h a k 2p D > 这表明,如果波包的大小比原胞尺寸大得多,晶体中电子的 运动就可以用波包的运动规律来描述。对于输运现象,只有 当电子平均自由程远大于原胞尺寸的情况下,才可以把晶体 中的电子当作准经典粒子,波包移动的速度(群速度)等于 处于波包中心处粒子所具有的平均速度

附录:更简明的说明: 量子力学告诉我们,晶体中处于业状态的电子,在经 典近似下,其平均速度相当于以k为中心的波包速度,而 波包的传播速度是群速度:,_ω(k) VE= ak 量子力学中的德布罗意关系:E=o 所以电子的平均速度: p= 1 aE(k ak
附录:更简明的说明: 量子力学告诉我们,晶体中处于 状态的电子,在经 典近似下,其平均速度相当于以 k0为中心的波包速度,而 波包的传播速度是群速度: 量子力学中的德布罗意关系: 所以电子的平均速度: ( ) g k v k ¶w = ¶ E = hw 1 E k( ) v k ¶ = h ¶ 0 yk