
第三章 光的干涉 3.1 光的干涉和相干条件 3.2 杨氏双缝干涉实验 3.3薄膜干涉 3.4 迈克尔逊干涉 3.5 时空相干性 3.6 多光束干涉
第三章 光的干涉 3.1 光的干涉和相干条件 3.2 杨氏双缝干涉实验 3.3 薄膜干涉 3.4 迈克尔逊干涉 3.5 时空相干性 3.6 多光束干涉

3.1、光的干涉和相干条件 B ·在波的叠加原理成立的条件下,根据交叠区中光强分布可分为两种 情况: 。非相千叠加:观测时间中总光强是各分光强直接相加 I(P)=I1(P)+I2(P) 。相千叠加:观测时间中总光强不等于各分光强直接相加 I(P)=I1(P)+I2(P)+△(P) 通常表现为交叠区中出现了明暗相间的千涉条纹,即光强有了重新 分布。 号=E+20+2E10E20cos(p2-p1) 当两束或者两束以上光波在一定条件下相遇而叠加,出现了明暗相间或者 彩色的条纹,这种现象称为光的干涉
3.1、光的干涉和相干条件 当两束或者两束以上光波在一定条件下相遇而叠加,出现了明暗相间或者 彩色的条纹,这种现象称为光的干涉

为什么会发生光的干涉现象?(光强为何会重新分布?) I(P)=(E路〉=(E1+E2)2〉=(E+码+2EE2〉 ∴.I(P)=(〉+()+2(1E2)=I1(P)+I2(P)+△I(P) 最后一项为干涉项,是决定是否相干的关键项! △I(P)=2(E1E2〉 干涉项 ={8给经+ ,非相干叠加,非相干光 ,相干叠加,相干光

3.1.1、光的相千条件 什么条件下发生光的干涉现象? ★必要条件: 。同频率。同振向(或分量)。空间有稳定的相位差分布 女充分条件:两振幅差不多 是否相干←→2(B1E2)是否为0 高1=瓦10cos(w1t-k1r1-p10) =E20 cos(wat-kar2-p20)
3.1.1、光的相干条件
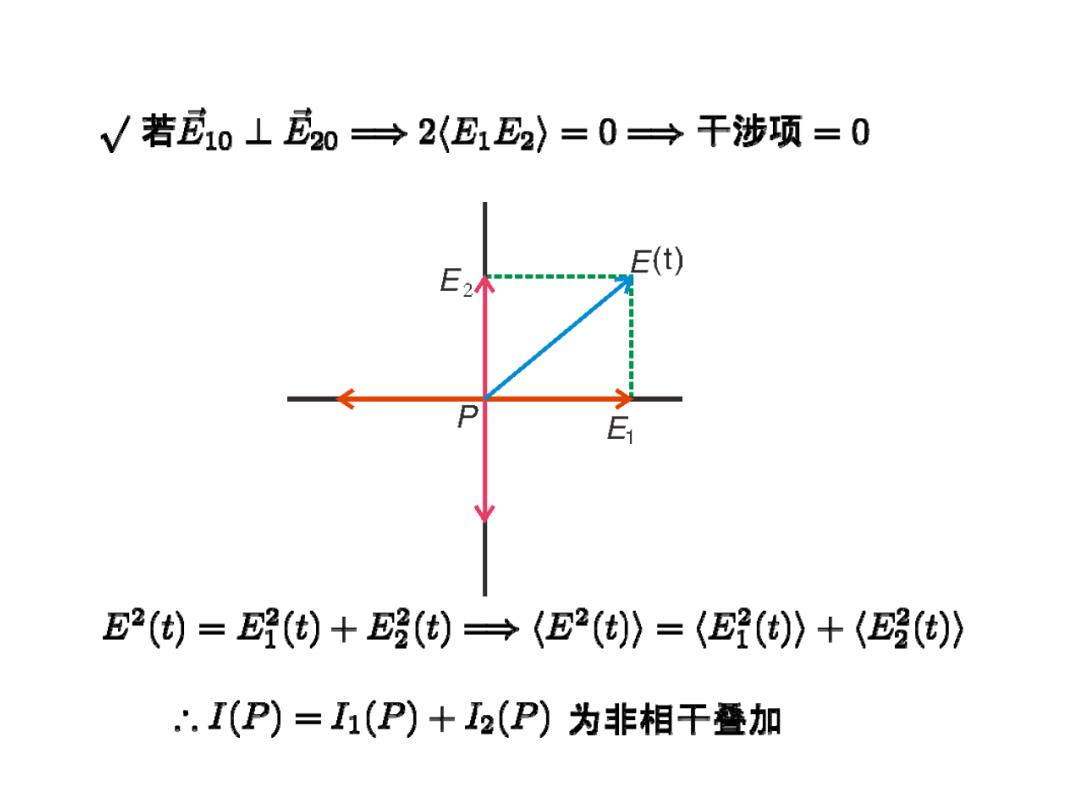
√若10⊥20→2(E1E2〉=0→干涉项=0 E2 E(t) E2(t)=()+E()→(E2()》=(()》+((t)》 ∴.I(P)=I1(P)+I2(P)为非相干叠加

√若瓦10‖瓦0但w1≠w2 2(EE2〉=2(瓦0·成0co(u1t-2十p)·cos(2t-2g+p20》 =oE20(o8(w1+w2)t-(p1+p2)+c0s(w1-2)t-(p1-p2) =0 (余弦函数,取周期平均=0) √w1=w2,0‖瓦20(同频,同振向) 当w1=w2时,有 2(1·E2)=E10E20cos(p2(P)-p1(P)卡0

I=I1+I2+2VI1I2 Co86(P) 光强分布基本公式 其中6(P)=p2(P)-p1(P)=k(r2-r1)-(p20-p10) 为两列光波在空间点的相位差分布,含两项! √√空间有稳定的相位差分布 不同光源(不同原子)发出的光的叠加(w1=w2=w,瓦0‖瓦20) *1 10 6(P)=k(r2-r1)-(p50-p5o) ·P后一项在0心2π间随即变化 20 cos(P)=cos(k(r2-r1)-(spo-io)) =cos(f()=0 →I合=I1+I2→非相干叠加

√充分条件(使干涉条纹明显)E10~20 定义:反衬度(可见度) IM-Im 2 2VT112 IM+Im I1+I2 →E10ND20 →I1=2→Y=1 20>10: →I2>I1→Ym0 I=I1+I2+2VI1I2co86(P)=(I1+I2)(1+Yco86(P) Y=0→I=I1+I2,非相干叠加!

。必要条件一:频率相同 。必要条件二:振动方向一致或有平行的振动分量 。必要条件三:相位差在观察时间内稳定分布 。条件一适用所有波动,条件二仅适用矢量波,条件三对光波的干涉 尤为重要。 ·还有一个充分条件:参与相干的光振幅大致差不多。 。双光束千涉 I(P)=11(P)+12(P)+2VI12cos8(P)

3.1.2、干涉的相位差和光程差判据 •光的干涉的具体规律 >光强的空间分布 I(P)=I1(P)+I(P)+2I1I cos6(P) ◆明暗条紋位置-相位差判据 ={ x 亮条纹 (2m+1) 暗条纹 (m=0±1,±2,…) ·光程差判据 若两列光波经过两种介质,甚至不均匀介质→(P)=? 6(P)= 2mr1(P)_2r2(P) 入1 2
3.1.2、干涉的相位差和光程差判据