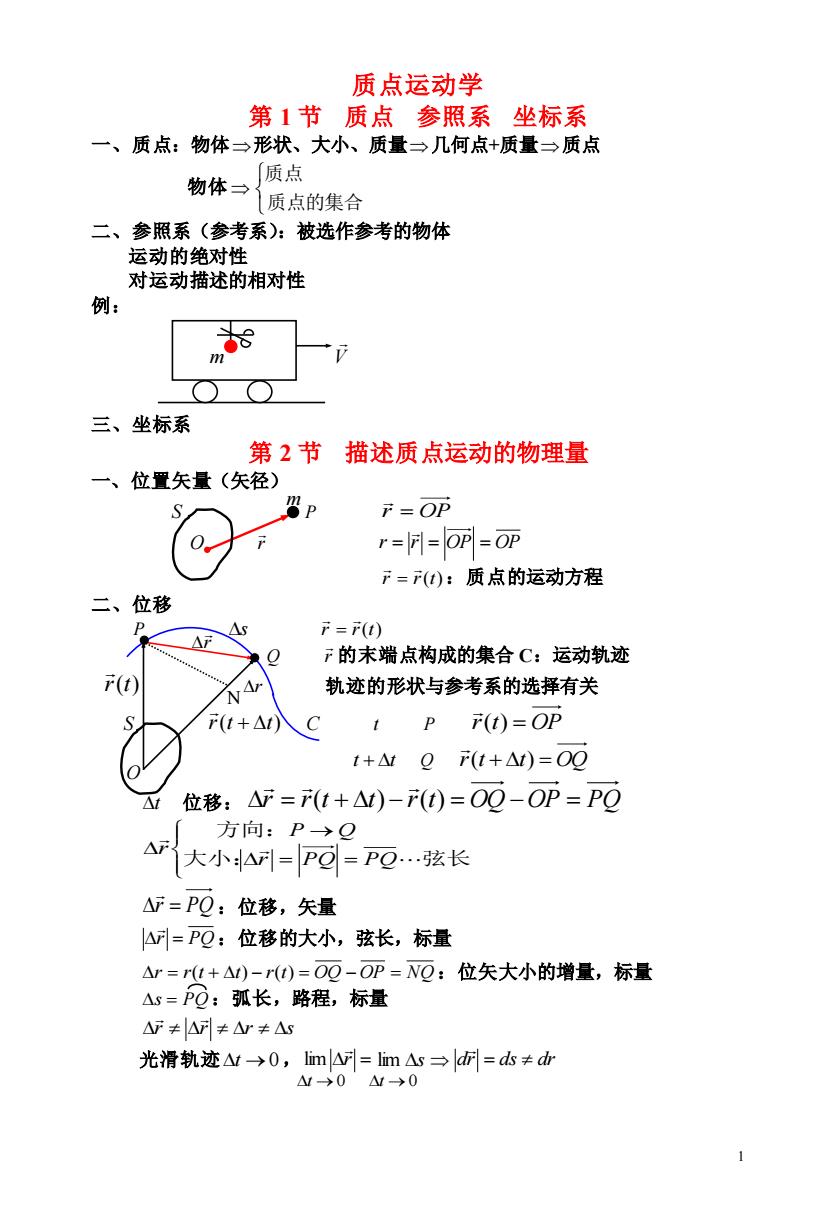
质点运动学 第1节质点参照系坐标系 一、质点:物体一形状、大小、质量一几何点+质量→质点 物体三质点 质点的集合 二、参照系(参考系):被选作参考的物体 运动的绝对性 对运动描述的相对性 例: m 三、坐标系 第2节 描述质点运动的物理量 一、位置矢量(矢径) S F=OP r==OP OP F=():质点的运动方程 二、位移 r=r(t) F的末端点构成的集合C:运动轨迹 (t) 轨迹的形状与参考系的选择有关 F(t+△1) t (t)=OP t+△tQ(t+△)=OO 位移:=(t+△)-(t0)=OQ-OP=PO 方向:P→Q 大小A=P@-Po…弦长 △F=PQ:位移,矢量 △=PQ:位移的大小,弦长,标量 △r=(t+△)-r()=O0-OP=N0:位矢大小的增量,标量 △s=PQ:弧长,路程,标量 △≠△≠山≠△s 光滑轨迹△t→0,liml△=lim△s→ld耐=dk≠d △1→0△1→0
1 t →0 质点运动学 第 1 节 质点 参照系 坐标系 一、质点:物体 形状、大小、质量 几何点+质量 质点 物体 质点的集合 质点 二、参照系(参考系):被选作参考的物体 运动的绝对性 对运动描述的相对性 例: m V 三、坐标系 第 2 节 描述质点运动的物理量 一、位置矢量(矢径) S P r = OP O r r = r = OP = OP r r(t) = :质点的运动方程 二、位移 P s r r(t) = Q r 的末端点构成的集合 C:运动轨迹 r(t) 轨迹的形状与参考系的选择有关 S r(t + t) C t P r(t) = OP t + t Q r(t + t) = OQ t 位移: r = r(t + t) − r(t) = OQ −OP = PQ = = → 大小: 弦长 方向: r PQ PQ P Q r r = PQ :位移,矢量 r = PQ :位移的大小,弦长,标量 r = r(t + t) − r(t) = OQ − OP = NQ :位矢大小的增量,标量 s = PQ :弧长,路程,标量 r r r s 光滑轨迹 t →0, r = lim lim s dr = ds dr O m r r N t →0

三、速度 1、平均速度:下= △t 方向: △ 大如照:名岁 △t △t△ 2、(瞬时)速度 速度FmF=mg=正=f0 At0)0△1di 「方向:轨迹的切向,指向质点运动方向 大小:连率月因园会 ~li=d≠dhr= di di 平均速率7为 ≠As 严≠同 四、加速度 1、平均加速度 7(t) 1, P V(t) t+△t Qt+△) (t+△) △r速度增量:△=(t+△)-() 注意:△V与△V的区别 (t+△t) △7:矢量 速率增量:△V=V(t+△)-V(),标量 △V≠A,dW≠la 方向:沿△的方向 平均加速度:后=A严 △1 天小 2、(瞬时)加速度 加速度a-lima=lim △di_d,f、-d27 w→0△→0△1ddd'd2 方向: 一般指向轨迹凹的一侧 大=-- dt 2
2 三、速度 1、平均速度: t r V = V = = = t s t r t PQ t r t r V r 大小 方向: 2、(瞬时)速度 速度 lim lim V(t) dt dr t r V V = = = = = = = = dt ds dt dr dt dr V V V V 的大小:速率 方向:轨迹的切向,指向质点运动方向 dr = ds dr dt dr dt ds V = 平均速率: t s V = r s V V 四、加速度 1、平均加速度 P V (t) t , P V (t) V t + t Q V(t + t) V(t + t) t 速度增量: V V(t t) V(t) = + − S V 注意: V 与 V 的区别 O V(t + t) V :矢量 速率增量: V = V(t + t) −V(t) ,标量 V V , dV dV 平均加速度: t V a = = = t V t V t V a V 大小: 方向:沿 的方向 2、(瞬时)加速度 加速度 2 2 lim lim ( ) dt d r dt dr dt d dt dV t V a a = = = = = = = = dt dV dt dV dt dV a a a 大小: 方向: 一般指向轨迹凹的一侧 Q t →0 t →0 t →0 t →0

第3节、△F、、ā在直角坐标系中的表示 一、位矢 F-xi+万+zk P(x,y,z) r=F=vx2+y2+32 cosa=,cosB=,cosy= cos2a+cos2β+cos2y=1 i=(t)=x=x(t),y=y(t),=z(t) 消去时间变量可得轨迹方程 二、位移: 产()=x(t)i+y()j+z()k (t+△)=xt+△r)i+yt+△)j+zt+△)k △F=F(t+△)-F(t)=△xi+△y+△k 三、速度:下_而+少j+止x dt dt dtdt dt v= V=Vi+v,j+vk dt dt r闭=及++顶=++ 四、加速度 a-d亚_-业i+j+水x dt 23 dv,d'x ax= dhdh2’a,= 三= dt a=a,i+a,j+ak,a=a=a+a;+a 例:已知:)=327+412 求:(1),V,,:(2)t=ls~t2=2s,f,0,(2) 解:(1)f-正=6i+12r27,V=61,,=12 (2)F0=3i+4j,(2)=12i+32j N=0-70=97+287,7-g=7+28 7)=6i+12ji,(2)=12i+48 3
3 第 3 节 r 、 r 、V 、 a 在直角坐标系中的表示 一、位矢 z r xi yj zk = + + P(x, y,z) 2 2 2 r = r = x + y + z r r x cos = , r y cos = , r z cos = S cos cos cos 1 2 2 2 + + = O j y r r(t) = x = x(t), y = y(t), z = z(t) i 消去时间变量可得轨迹方程 x 二、位移: r t x t i y t j z t k ( ) = ( ) + ( ) + ( ) r t t x t t i y t t j z t t k ( + ) = ( + ) + ( + ) + ( + ) r = r(t + t) − r(t) = xi yj zk + + 三、速度: k dt dz j dt dy i dt dx dt dr V = = + + ( = = = 0 dt dk dt dj dt di ) dt dx Vx = , dt dy Vy = , dt dz Vz = , V V i V j V k x y z = + + 2 2 2 2 2 2 ( ) ( ) ( ) dt dz dt dy dt dx V = V = Vx +Vy +Vz = + + 四、加速度 k dt d z j dt d y i dt d x k dt dV j dt dV i dt dV dt d r dt dV a x y z 2 2 2 2 2 2 2 2 = + + = = = + + 2 2 dt d x dt dV a x x = = , 2 2 dt d y dt dV a y y = = , 2 2 dt d z dt dV a z z = = a a i a j a k x y z = + + , 2 2 2 a = a = ax + ay + az 例:已知: r t t i t j 2 3 ( ) = 3 + 4 求:(1) V ,Vx ,Vy ;(2) t 1s ~ t 2s 1 = 2 = ,V ,V (1) ,V (2) 解:(1) ti t j dt dr V 2 = = 6 +12 ,V t x = 6 , 2 V 12t y = (2) r i j (1) = 3 + 4 , r i j (2) =12 + 32 r r r i j = (2) − (1) = 9 + 28 , i j t r V = 9 + 28 = V (1) = i j 6 +12 ,V (2) = i j 12 + 48 k

例:x=Rcos@t,y=Rsin ot,o,R为常量 求:(1)任意时刻、、ā(2)轨迹方程 解:(1)F=xi+y=Rcosoti+Rsin @tj F-正-oRsin wfi+oRcoswj,V=aR恒定 dt d a- -=-@2Rcosoti-@2Rsin otj=-@2F d (2)x2+y2=R2 必女兴兴央兴女必兴央兴必必兴兴兴光兴兴兴兴必兴兴必兴女必兴兴兴女头兴兴兴兴头兴兴兴出兴必必兴必兴必必兴女头必兴兴 一维直线运动 一x x=f(t) 盘:r安公,,速度 V>0,速度沿x轴正方向,V<0,速度沿x轴负方向 。会0出 dtd, a:加速度 a,V同方向,加速运动,a,V反方向,减速运动 *出★必*★必★必*必必必必★六★必★★0★必*六0六兴兴出0出★必必*必★必*0必*出★必★必必★六★必必★六 例:已知V=0),求1~1,这段时间内△F,△s,F,下,a 解:P=东=0→-r0t→f=0dh, =5-i=∫70)d r-密=pols=ioa-js-ioa △s=心Fold 币-心.0h巧+区 ΓM6-42 p-s.i0地+ △t12-4 2 a=AP=P()-v(),ata △1t2-t1 2 4
4 例: x = Rcost, y = Rsin t , ,R 为常量 求:(1)任意时刻 r 、V 、a (2)轨迹方程 解:(1) r xi yj R ti R tj = + = cos + sin R ti R tj dt dr V = = − sin + cos ,V =R 恒定 R ti R tj r dt dV a 2 2 2 = = − cos − sin = − (2) 2 2 2 x + y = R ******************************************************** 一维直线运动 x = f (t) = = dt df t dt dx Vx ( ) dt df t dt dx V ( ) = = , V :速度 V 0 ,速度沿 x 轴正方向, V 0 ,速度沿 x 轴负方向 2 2 dt d x dt dV a x x = = 2 2 dt d x dt dV a = = , a :加速度 a,V 同方向,加速运动, a,V 反方向,减速运动 ******************************************************** 例:已知 V V (t) = ,求 1 ~ 2 t t 这段时间内 r ,s ,V ,V ,a 解: = = V (t) dt dr V dr = V (t)dt = 2 1 2 1 ( ) t t r r dr V t dt , r = r2 − r1 = 2 1 ( ) t t V t dt = = V (t) dt ds V ds = V(t) dt = 2 1 ( ) t t ds V t dt = 2 1 ( ) t t s V t dt 2 ( ) 1 2 2 1 2 1 V V t t V t dt t r V t t + − = = 2 ( ) 1 2 2 1 2 1 V V t t V t dt t s V t t + − = = 2 ( ) ( ) 1 2 2 1 2 1 a a t t V t V t t V a + − − = = O x x