
第7节势能功能原理机械能守恒定律 一、保守力、保守力场 如果力作功仅与质点的始末位置有关,与质点走过的路径无关 或者,fF=0→保守力 非保守力 保守力场 二、势能 R R:参考点,「F而 M 定义:势能Ep(M)上「Fd而 m M 注意: 1、势能与功的区别 2、保守力场→势能,势能是质点与保守力场共同具有的 3、Ep(R)上「F.d而=O,参考点就是零势能点 4、势能只具有相对意义,R':Ep(M)上「F· Ep(M)≠Ep(M) 5、同一质点在保守力场中任意两点上势能的差值 与参考点的选择无关 R:Ep(M)-Ep(N) --j-F+i-f而 R':Ep(M)-Ep(N) --jf-小 Ep(M)-Ep(N)=EP(M)-EP(N) 6、保守力的功与势能变化的关系 4=jF=+jF亦=了F-jF =Ep(M)-Ep(N)=-IEP(N)-EP(M)=-AEP A=-△E,保守力作功等于势能增量的负值 A>0,Ep↓,A<0,Ep↑ 7、势能等于每一种势能的代数和 不同的保守力场参考点不必相同
1 第 7 节 势能 功能原理 机械能守恒定律 一、 保守力、保守力场 如果力作功仅与质点的始末位置有关,与质点走过的路径无关 或者, = L F dr 0 保守力 非保守力 保守力场 二、 势能 R :参考点, R M F dr 定义:势能 EP ( M )= R M F dr m 注意: 1、势能与功的区别 2、保守力场 势能,势能是质点与保守力场共同具有的 3、 EP ( R )= R R F dr =0,参考点就是零势能点 4、势能只具有相对意义, R : EP ( M )= R M F dr EP ( M ) EP ( M ) 5、同一质点在保守力场中任意两点上势能的差值 与参考点的选择无关 R : EP ( M )− EP ( N ) = R M F dr − R N F dr = R M F dr + N R F dr = N M F dr R : EP ( M ) EP − ( N ) = R M F dr − R N F dr = R M F dr + N R F dr = N M F dr EP ( M )− EP ( N )= EP ( M ) EP − ( N ) 6、保守力的功与势能变化的关系 = N M A F dr = R M F dr + N R F dr = R M F dr − R N F dr = EP ( M )− EP ( N )=-[ EP ( N )- EP ( M )]=- EP A = −EP ,保守力作功等于势能增量的负值 A 0, EP , A 0, EP 7、势能等于每一种势能的代数和 不同的保守力场参考点不必相同 N R R M
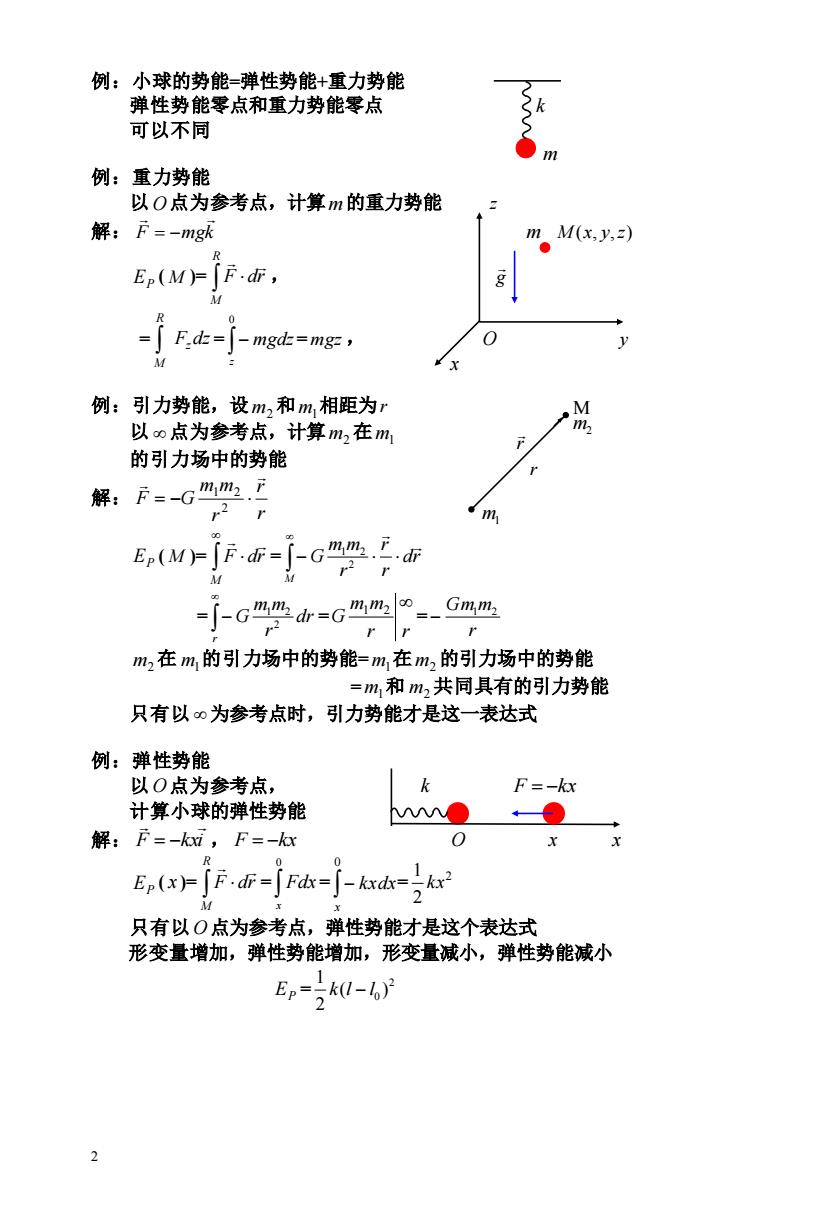
例:小球的势能=弹性势能+重力势能 弹性势能零点和重力势能零点 可以不同 例:重力势能 以O点为参考点,计算m的重力势能 解:F=-mgk mM(x,y,z) Ep(M)=「F.d, =了Fk=∫- mgdz=mgz, y M 例:引力势能,设m,和m相距为r M 以o点为参考点,计算m2在m1 m 的引力场中的势能 解:F=-Gmm2. r2 r m Ep(M∫Ff=「-Gmm.工.d而 =」-G"m=Gmm=-Gmm m2在m的引力场中的势能=m,在m2的引力场中的势能 =m,和m2共同具有的引力势能 只有以∞为参考点时,引力势能才是这一表达式 例:弹性势能 以O点为参考点, F=-kx 计算小球的弹性势能 M● 解:F=-kmi,F=- E(x)-Fd-Fd-J-kxdk 只有以O点为参考点,弹性势能才是这个表达式 形变量增加,弹性势能增加,形变量减小,弹性势能减小 Er-zk(-b) 2
2 例:小球的势能=弹性势能+重力势能 弹性势能零点和重力势能零点 k 可以不同 m 例:重力势能 以 O 点为参考点,计算 m 的重力势能 z 解: F mgk = − m M (x, y,z) EP ( M )= R M F dr , g = F dz z R M = − 0 z mgdz= mgz , O y 例:引力势能,设 m2 和 m1 相距为 r 以 点为参考点,计算 m2 在 m1 的引力场中的势能 解: r r r m m F G = − 2 1 2 EP ( M )= M F dr = − M dr r r r m m G 2 1 2 = − r dr r m m G 2 1 2 = r r m m G 1 2 = r Gm1m2 − m2 在 m1 的引力场中的势能=m1 在 m2 的引力场中的势能 = m1 和 m2 共同具有的引力势能 只有以 为参考点时,引力势能才是这一表达式 例:弹性势能 以 O 点为参考点, k F = −kx 计算小球的弹性势能 解: F kxi = − , F = −kx O x x EP ( x )= R M F dr = 0 x Fdx = − 0 x kxdx= 2 2 1 kx 只有以 O 点为参考点,弹性势能才是这个表达式 形变量增加,弹性势能增加,形变量减小,弹性势能减小 EP = 2 0 ( ) 2 1 k l − l x M m2 m1 r r

三、功能原理 A外+A内=△E=Ek2一E1 将内力划分为保守内力和非保守内力 A外十A保内+A非保内=Ek2一E对 A保内=-△Ep=-(EP2-EpI) A外+A保内=Ek2一E1十EP2一EPI =(Ek2+Ep2)-(Ek1+EpI) 定义:质点系的机械能:E=Ek+Ep A外+A非保内=E2一E,=△E:功能原理的积分形式 功能原理的微分形式为 dA外+dA非保内=dE 四、机械能守恒定律 如果仅有保守内力作功 1、仅有保守内力,没有外力,也没有非保守内力 dA外=dA非保内=0, dA外+dA非保内=0 2、有外力,也有非保守内力 dA外+d4非保内=0 E=C一机械能守恒定律 注意: 1、功能原理和机械能守恒定律只适用于惯性系 2、所谓某个物理量守恒是指这个物理量的数值 (对于矢量应包括它的大小和方向)始终保 持不变,仅仅是始末状态相等不叫守恒 例:求重物(重量P)自弹簧原长C点 4 无初速下滑至圆环最低点B时获得 k,1o=R 的动能,不计摩擦 解:取C点为弹性势能零点 60 B点重力势能零点 重物位于C点时的机械能为 R E1=P(R+Rcos60)=PR B 重物位于B点时的机械能为 E2=Ek+5k(2R-R)2 E,=E2 2PR-E+1KR 1 动能E 1 -PR--kR2 3
3 三、 功能原理 外 内 A + A = Ek = Ek 2 - Ek1 将内力划分为保守内力和非保守内力 外 保内 非保内 A + A + A = Ek 2 - Ek1 保内 A = − EP = ( ) − EP2 − EP1 外 非保内 A + A = Ek 2 - Ek1 + EP2 - EP1 =( Ek 2 + EP2 )-( Ek1 + EP1 ) 定义:质点系的机械能: E = Ek + EP 外 非保内 A + A = E2- E1 =E :功能原理的积分形式 功能原理的微分形式为 外 非保内 dA + dA = dE 四、 机械能守恒定律 如果仅有保守内力作功 1、 仅有保守内力,没有外力,也没有非保守内力 外 非保内 dA = dA =0, 外 非保内 dA + dA =0 2、 有外力,也有非保守内力 外 非保内 dA + dA =0 E = C 机械能守恒定律 注意: 1、 功能原理和机械能守恒定律只适用于惯性系 2、 所谓某个物理量守恒是指这个物理量的数值 (对于矢量应包括它的大小和方向)始终保 持不变,仅仅是始末状态相等不叫守恒 例:求重物(重量 P )自弹簧原长 C 点 无初速下滑至圆环最低点 B 时获得 k , l 0 = R 的动能,不计摩擦 C 解:取 C 点为弹性势能零点 60 B 点重力势能零点 O F 重物位于 C 点时的机械能为 R N E P R R PR 2 3 ( cos60 ) 1 = + = 重物位于 B 点时的机械能为 P 2 2 (2 ) 2 1 E = Ek + k R − R E1 = E2 2 2 1 2 3 PR = Ek + kR 动能 2 2 1 2 3 Ek = PR − kRB A