西安电子科技大学：《大学物理》课程教学讲义（下）10-9 电容 电容器

第3节电容 电容器 一、孤立导体的电容 Uocq, =C:电容 U SI:CV=F(法拉) 例：导体球 解：U=9 4πE,R C=9=4r6R U C地=4π6R=4π×8.85×10-12×6400×103≈7.0×104(F) U=4πE5,R C=4=466,R=c,C0 U R 二、 电容器及电容 UAB=UA-UB goUB 9=C U UAB SI:F(法拉) A(正极板) B(负极板) 三、几种典型的电容器 1、平行板电容器 Q E=Eo=a Q E.oE EoE S D.dS=DAS=ONs, +H D=G=808,E, E=G=0 Eofr Eo,S Un=Ed=-2 d Eo&S 2=6,C0,C0=1 oS UAB d d 1

1 第 3 节 电容 电容器 一、孤立导体的电容 U  q ， q C :电容 U q  U SI：C/V=F（法拉） 例：导体球 解： R q U 4 0   O q   U q C0 4 0R R U C地  4 0R = 4 8.8510 12  640010 3  7.010 4 （F） R q U r   4 0  r    = U q C 4 0 rR rC0  二、电容器及电容 UAB  UA UB q  q q UAB C U q AB  UA r  UB SI：F（法拉） A (正极板) B (负极板) 三、几种典型的电容器 1、平行板电容器 S E Q E r r r       0 0 0    S = = ，   S D dS   DS S S D   = E ， r  0 r  S Q E r r      0 0   d d S Q U Ed r AB  0   0 C0 ， d S U Q C r r AB       d S C 0 0   Q  Q A B R O q

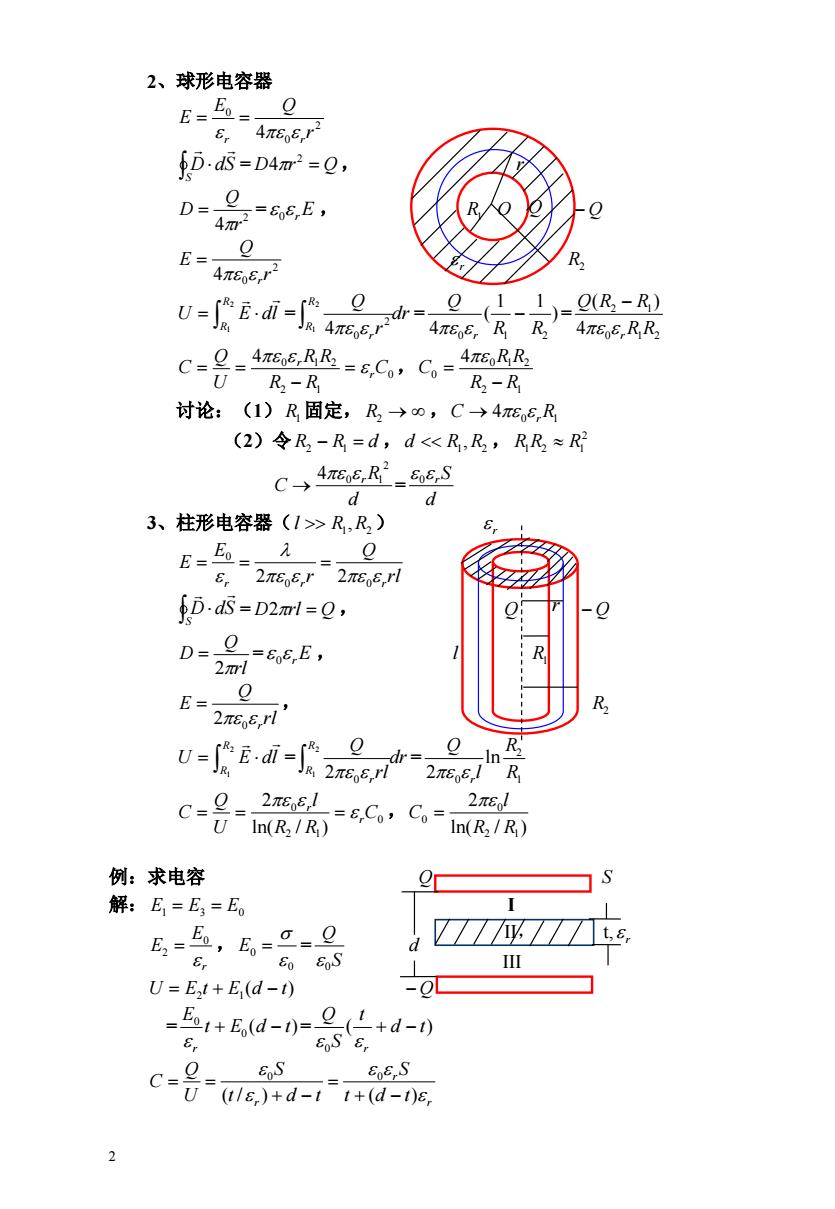
2、球形电容器 E=5o=_ Q EoEr2 fD5=D4m2=0, D= 40=66E, E=- Q 4n66,r2 R u-i-j9 L-)=B-R) 4πE5,RR,4πES,RR C-2-4TEo6,RRs=BCo,Co- π6RR U R-R R-R 讨论：（1)R固定，R2→0，C→4πo6,R (2)令R-R=d,dR,R) E=E= 、Q 8.2πE6,r2πEoE,rl D.dS=D2ml=2, D= 2ml =65,E, E=0 R 2πEo6,rl d B可2”2ce7 CC CoIm(R/R) 、2πEl U In(R2/R) 例：求电容 解：E,=E3=Eo E,=,E=g=9 d 8, Eo oS I U=E,t+E(d-t) -OL =+E(d-0=g(←+d-0 Er 6S`6, 86,S C221e)+d-1t+(d-g EoS 2

2 2、球形电容器 2 0 0 4 r E Q E r r      = ，   S D dS   D r  Q 2 4 r = ， 2 4 r Q D    0 rE R1 O  Q 2 0 4 r Q E r    r  R2 = = =    2 1R R U E dl   dr r R Q R r  2 1 2 4 0   ) 1 1 ( 4 0 R1 R2 Q r    0 1 2 2 1 4 ( ) R R Q R R r   0 ， 2 1 4 0 1 2 C R R R R U Q C r r        2 1 0 1 2 0 4 R R R R C    讨论：（1） R1 固定， R2   ，C 4 0 rR1    （2）令 R2  R1  d ，d  R1 ,R2 ， 2 R1R2  R1 = d R C r 2 4 0 1    d Sr  0 3、柱形电容器（ ） 1 2 l  R ,R r  rl Q r E E r r r       0 0 0 2 2    = ，   S D dS   D2rl  Q Q  Q = ， rl Q D 2   0 rE l R1 ， rl Q E r   2 0  R2 = =    2 1R R U E dl   dr rl R Q R r  2 1 2 0   1 2 0 ln 2 R R l Q r   0 ， 2 1 0 ln( / ) 2 C R R l U Q C r r       ln( / ) 2 2 1 0 0 R R l C   例：求电容 Q S 解： I E1  E3  E0 ， = r E E  0 2  0 0   E  S Q 0  d ( ) 2 1 U  E t  E d  t  Q = 0 ( )= 0 t E d t E r    ( ) 0 d t t S Q r     r r r t d t S t d t S U Q C      ( / ) ( ) 0 0        r II， t, r  III Q

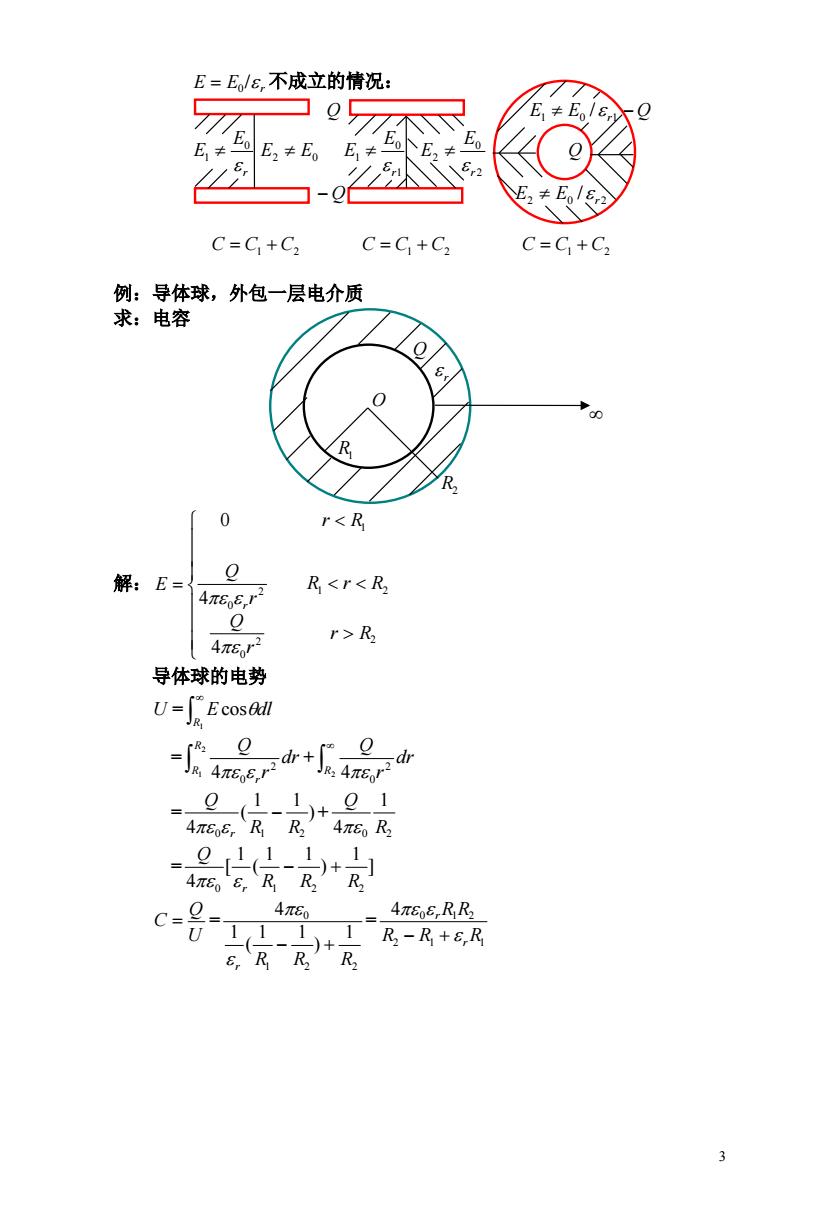
E=E/8,不成立的情况： 不 E1 EE,≠E0 E,≠ -6 C=C+C2 C=C+C2 C=C+C2 例：导体球，外包一层电介质 求：电容 R 0 rR 导体球的电势 U-Ecosll Q d+、 dr Q JR24πEr Q 1、Q1 4πE,RR 4π6R 4π6,RR R 4π60 c=光=11T 4π68，RR2 1 )+ R-R+ER ER R2 R2 3

3 E  E0 / r 不成立的情况： Q 1 0 1 / E E r    Q r E E  0 1  E2  E0 1 0 1 r E E   2 0 2 rE E   Q  Q 2 0 2 / E E r   C  C1  C2 C  C1  C2 C  C1  C2 例：导体球，外包一层电介质 求：电容 解：           2 2 0 2 1 2 0 1 4 4 0 r R r Q R r R r Q r R E r    导体球的电势 U =  1 cos R E dl = +  2 1 2 4 0 R R r dr r Q    2 2 4 0 R dr r Q  = ) + 1 1 ( 4 0 R1 R2 Q r    0 2 1 4 R Q  = ] 1 ) 1 1 ( 1 [ 4 0 R1 R2 R2 Q r     = = U Q C  1 2 2 0 1 ) 1 1 ( 1 4 r R R R     2 1 1 4 0 1 2 R R R R R r r      O R1 R2 Q r  

第4节 电场的能量 一、带电体的静电能 dq 已搬运的电荷q在dg所在 位置产生的电势(q) 搬运d过程外力克服电场力 作功dA=(q)dg 外力克服电场力作功的总和：静电能 =2g)d西 例：孤立导体球的静电能 解：u= 9 dq 4πenR udg=、9 4πEnR W=uayd dq -R肉 03 TEOR 二、电容器的能量 已搬运的电荷q X 电势差u4B=q/C 搬运dg过程外力克服电场力 da 作功dA=uandq 外力克服电场力作功的总和： 电容器的能量 Ag C-gB 2,VAB,Q=CVAB 电容器储能公式 对任意的电容器成立 孤立导体球：C=4π6，R,W= 2C8π6，R 带电系统的能量就是它的电场的能量 三、电场的能量 C=50E,S d ，VAB=Ed w= =、C 2C2 AB =16,S (Ed)2, 2 d 22E2S=22 4

4 第 4 节 电场的能量 一、带电体的静电能 Q dq 已搬运的电荷q 在dq 所在 q 位置产生的电势u(q) 搬运dq 过程外力克服电场力 作功dA  u(q)dq 外力克服电场力作功的总和：静电能   Q W u q dq 0 ( ) 例：孤立导体球的静电能 解： ， R q u 4 0   dq R q udq 4 0   Q q   Q W u q dq 0 ( ) O dq = = 。 Q dq R q 0 4 0  R Q 0 2 8 R 二、电容器的能量 Q  Q 已搬运的电荷q 电势差uAB  q /C 搬运dq 过程外力克服电场力 作功dA  uABdq 外力克服电场力作功的总和： 电容器的能量 A q C  q B   = = ， ， ， Q W uABdq 0 Q dq C q 0 C Q 2 2 Q VAB Q  CVAB = = 电容器储能公式 C Q W 2 2  QVAB 2 1 2 2 1 CVAB 对任意的电容器成立 孤立导体球：C  4 0R， = C Q W 2 2  R Q 0 2 8 带电系统的能量就是它的电场的能量 三、电场的能量 Q d  Q ， d S C r  0  VAB  Ed S = C Q W 2 2  2 2 1 CVAB = ， 0 2 ( ) 2 1 Ed d   rS r  = rE Sd rE V 2 0 2 0 2 1 2 1      dq u(q)

能量分布在电场中 E 电场是能量的携带者 d形 电场能量密度 dw dy W= 形-26e,E=DE=)D.E,wxE dw_1 均匀电场，W=wV 非均匀电场，dW=wdW w-fdw=fwdv-fdv 例：孤立导体球电场的能量 dr dy 4nr'dr 0 rR 0 rR 32π26r w-fwdv -fgv+gv 8πEnR 静电学，静电能一电容器的能量一电场能量 计算带电系统静电能或电场能量的方法： (1)电容器， w=02 28 (2)已知E，W=wd=e,Ed" (3)搬运方法，m=gd山 w-c.E>0,w=小nd>0

5 能量分布在电场中 E  电场是能量的携带者 dW 电场能量密度 dV dV dW w  = ， dV dW w  rE DE D E      2 1 2 1 2 1 2 0   2 w  E 均匀电场，W  wV 非均匀电场，dW  wdV =     V W dW wdV V rE dV 2 0 2 1   例：孤立导体球电场的能量 dr r dV r dr 2  4 Q O R 解：         r R r Q r R E 2 4 0 0           r R r Q r R w rE 4 0 2 2 2 0 32 0 2 1             V r R r R W wdV wdV wdV = r dr = r Q R 2 4 0 2 2 4 32     R Q 0 2 8 静电学，静电能 电容器的能量 电场能量 计算带电系统静电能或电场能量的方法： （1）电容器， C Q W 2 2  （2） 已知 E ， =    V W wdV V rE dV 2 0 2 1   （3）搬运方法，   Q W u q dq 0 ( ) 0 ， 2 1 2 w   0 rE    0 V W wdV