
第6节光的衍射 惠更斯-菲涅耳原理 一、光的衍射 当光遇到障碍物时能改变传播方向并绕过障碍物的边缘前进 ·:心· 1、菲涅耳衍射 2、夫琅和费衍射 光源、障碍物、屏相距有限远 光源、障碍物、屏相距无限远 二、惠更斯菲涅耳原理 惠更斯原理:波在媒质中传播到达的各点,可以看作发射子波的 波源,其后任意时刻,这些子波的包络面就是新的 波阵面 “从同一波面上各点发出的子波经传播在空间相遇时将产生相干 迭加” 惠更斯菲涅耳原理 dE=FK(0)d -cos(-) K():倾斜因子 0:n、F夹角 B=0,K(0)=1,0↑,K(0)J 0≥7,K0=0 机械波,E:位移;电磁波,E:电场强度 E-JdE-J FK(O)dS cos-) 波或光的传播都是按照惠更斯菲涅耳原理的方式进行的 第7节 单缝夫琅和费衍射 一、光路图 中:衍射角 二、衍射花样,p226 衍射条纹:与狭缝平行的直条纹 中央明纹最亮最宽
1 第 6 节 光的衍射 惠更斯-菲涅耳原理 一、光的衍射 当光遇到障碍物时能改变传播方向并绕过障碍物的边缘前进 S S K E K E 1、菲涅耳衍射 2、夫琅和费衍射 光源、障碍物、屏相距有限远 光源、障碍物、屏相距无限远 二、惠更斯-菲涅耳原理 惠更斯原理:波在媒质中传播到达的各点,可以看作发射子波的 波源,其后任意时刻,这些子波的包络面就是新的 波阵面 “从同一波面上各点发出的子波经传播在空间相遇时将产生相干 迭加” 惠更斯-菲涅耳原理 cos ( ) ( ) c r t r K dS dE F n K( ) :倾斜因子 dS :n 、 夹角 r dE =0, K( ) =1, , K( ) S P , =0 2 K( ) 机械波, E :位移;电磁波, E :电场强度 S c r t r K dS E dE F cos ( ) ( ) 波或光的传播都是按照惠更斯-菲涅耳原理的方式进行的 第 7 节 单缝夫琅和费衍射 一、光路图 :衍射角 A P O B 二、衍射花样,p226 衍射条纹:与狭缝平行的直条纹 中央明纹最亮最宽 r

向两侧明纹亮度越来越低,中央明纹是其余明纹宽度的两倍 三、菲涅耳半波带法 △S B /2 狭缝上下边缘发出的倾角为中的两条光线到达P点的光程差 6=BC=asin 每个波带的宽度△s= 元/2元 sin 2sin 狭缝被分割为波带的数目N=口-2asin单 △s 宽度为△= 的波带上下边缘发出的倾角为中的两条 2sino 光线到达P点的光程差恰为入/2,故名半波带 1一定,△s与中有关 相邻的两个半波带在P点引起的合振动干涉相消 1、衍射方程 a、2一定,N=N(),中个,△s↓,N↑ N=2asin .=±2k k=1,2,3,… asin=±kz k=1,23…, 暗纹 N=2asing =±(2k+1) k=1,2,3, asnp=2k+)月 k=1,2,3,… 明纹 明纹强度来自一个半波带的贡献 中个,△s↓,半波带面积↓,明纹强度↓ k:衍射级 asin=0外 中央明纹 3入 2 2 3 sino 0 0 2
2 向两侧明纹亮度越来越低,中央明纹是其余明纹宽度的两倍 三、菲涅耳半波带法 A A P a C B B / 2 狭缝上下边缘发出的倾角为 的两条光线到达 P 点的光程差 BC asin 每个波带的宽度 sin 2sin / 2 s 狭缝被分割为波带的数目 2asin s a N 宽度为 的波带上下边缘发出的倾角为 的两条 2sin s 光线到达 P 点的光程差恰为 / 2,故名半波带 一定,s 与 有关 相邻的两个半波带在 P 点引起的合振动干涉相消 1、衍射方程 a 、 一定, N N(), ,s , N 2 1,2,3, 2 sin k k a N asin k k 1,2,3,暗纹 (2 1) 1,2,3, 2 sin k k a N 1,2,3,,明纹 2 asin (2k 1) k 明纹强度来自一个半波带的贡献 ,s ,半波带面积 ,明纹强度 k :衍射级 asin 0:中央明纹 I 0 , a 3 a 2 a a a 2 a 3 sin s

2、条纹中心在屏上的位置 x=f.tg中≈f.sin中 暗纹中心坐标x=f·sinp=±kf k=1,2,3 明纹中心坐标x=f:sin功=士(2k+) k=123. 2a 中央明纹宽度(±1级暗纹间距)Ax。=-~巴)-22 第k级明纹的宽度Ax:=(W+1)户-k2-么 1一定,a个,△r↓ a>入,衍射效应不明显,a越小,衍射效应越显著 a一定,2不同,△x不同 日光,中央明纹:白色,两侧:彩色条纹 3、半角宽:中央明纹对透镜中心张角的一半或一级暗纹 对应的衍射角:中=arcsin2、 a a 4、圆孔的夫琅和费衍射 条纹呈环状 中央是一亮斑:爱里斑 爱里斑的半角宽0=122,D:圆孔直径 例:6=BC=asin,若P点为 第k级暗纹,则狭缝可以被 划分为多少个半波带? 若P点为第k级明纹,则狭 缝可以被划分为多少个半波带? 解:N=BC=2asin0 B 1/2元 若P点为第k级暗纹,asin中=k,N=2k 若P点为第k级明纹,asim0=(2k+1)号,N=2k+1
3 2、条纹中心在屏上的位置 x x P x O f x f tg f sin 暗纹中心坐标 sin k 1,2,3 a f x f k 明纹中心坐标 1,2,3 2 sin (2 1) k a f x f k 中央明纹宽度(1级暗纹间距) a f a f a f x 2 ( ) 0 第k 级明纹的宽度 a f a f k a f x k k ( 1) 一定,a ,x a ,衍射效应不明显,a 越小,衍射效应越显著 a 一定, 不同,x 不同 日光,中央明纹:白色,两侧:彩色条纹 3、半角宽:中央明纹对透镜中心张角的一半或一级暗纹 对应的衍射角: a a arcsin 4、圆孔的夫琅和费衍射 条纹呈环状 中央是一亮斑:爱里斑 爱里斑的半角宽 , :圆孔直径 D 1.22 D 例: BC asin ,若 P 点为 第k 级暗纹,则狭缝可以被 划分为多少个半波带? A P 若 P 点为第k 级明纹,则狭 缝可以被划分为多少个半波带? a 解: 2 sin / 2 BC a N B 若 P 点为第k 级暗纹,asin k , N 2k 若 P 点为第k 级明纹, ,2 sin (2 1) a k N 2k 1 C
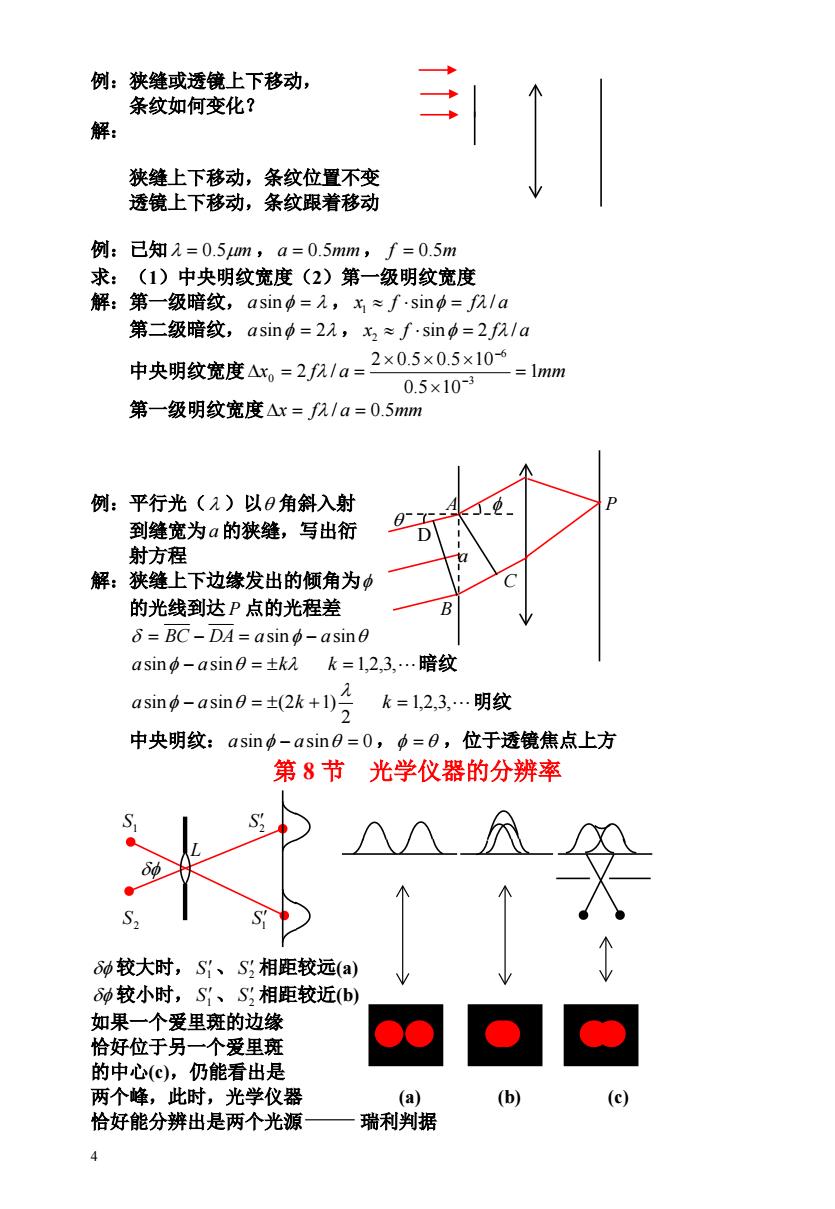
例:狭缝或透镜上下移动, 条纹如何变化? 解: 狭缝上下移动,条纹位置不变 透镜上下移动,条纹跟着移动 例:已知入=0.5m,a=0.5mm,f=0.5m 求:(1)中央明纹宽度(2)第一级明纹宽度 解:第一级暗纹,asin中=,x≈fsin中=f八la 第二级暗纹,asin=2,x2≈f·sin中=2fn/a 中央明纹宽度Ax。=2a/a=2×0.5×0.5x10 -=1mm 0.5×10-3 第一级明纹宽度△x=f/a=0.5mm 例:平行光(1)以0角斜入射 到缝宽为a的狭缝,写出衍 8-7 射方程 解:狭缝上下边缘发出的倾角为中 的光线到达P点的光程差 B δ=BC-DA=asin-asin0 asinφ-asin=±k 1k=12,3..暗纹 asing-asin0=±(2k+1)3 k=1,2,3,.明纹 中央明纹:asin中-asin0=0,=0,位于透镜焦点上方 第8节 光学仪器的分辨率 S2 6沙较大时,S1、S2相距较远(a) 6冲较小时,S1、S;相距较近(b) 如果一个爱里斑的边缘 恰好位于另一个爱里斑 的中心(c),仍能看出是 两个峰,此时,光学仪器 (a) (b) (c) 恰好能分辨出是两个光源 瑞利判据
4 例:狭缝或透镜上下移动, 条纹如何变化? 解: 狭缝上下移动,条纹位置不变 透镜上下移动,条纹跟着移动 例:已知 0.5m ,a 0.5mm, f 0.5m 求:(1)中央明纹宽度(2)第一级明纹宽度 解:第一级暗纹,asin , x1 f sin f / a 第二级暗纹,a sin 2 , x2 f sin 2 f / a 中央明纹宽度 x f a 1mm 0.5 10 2 0.5 0.5 10 2 / 3 6 0 第一级明纹宽度x f / a 0.5mm 例:平行光( )以 角斜入射 A P 到缝宽为a 的狭缝,写出衍 射方程 a 解:狭缝上下边缘发出的倾角为 C 的光线到达 P 点的光程差 B BC DA asin asin asin asin k k 1,2,3,暗纹 1,2,3,明纹 2 asin a sin (2k 1) k 中央明纹:asin asin 0, ,位于透镜焦点上方 第 8 节 光学仪器的分辨率 S1 2 S S2 1 S 较大时, 、 相距较远(a) 1 S S2 较小时, 、 相距较近(b) 1 S S2 如果一个爱里斑的边缘 恰好位于另一个爱里斑 的中心(c),仍能看出是 两个峰,此时,光学仪器 (a) (b) (c) 恰好能分辨出是两个光源 瑞利判据 L D

两个光源对小孔的张角恰好等于一个爱里斑的半角宽 0=1222:最小分辨角 0 Rs、1 :光学仪器的分辨本领(分辨率) 5o R=D 1.22元 ,RcD,Rc 例:人的瞳孔直径D≈3mm 求:人眼睛的最小分辨角?,用1=5500A的黄绿光计算 解:60=1.22-122×5500×10-0 =2.2×10-4rad 3×10-3 若黑板上有两条直线相距d=lcm, 请问,人离黑板多远时,恰能分辨 d =1cm 出是两条直线? 的=d, 6地人 s=d/0=1x102 2.2x10=45.5m 5
5 两个光源对小孔的张角恰好等于一个爱里斑的半角宽 = :最小分辨角 D 1.22 :光学仪器的分辨本领(分辨率) 1 R , , 1.22 D R R D 1 R 例:人的瞳孔直径 D 3mm 求:人眼睛的最小分辨角?,用 的黄绿光计算 5500A 解: = = D 1.22 rad 4 3 10 2.2 10 3 10 5500 10 1.22 若黑板上有两条直线相距d 1cm, 请问,人离黑板多远时,恰能分辨 出是两条直线? = , s d s s d 45.5m 2.2 10 1 10 / 4 2 d 1cm