西安电子科技大学：《大学物理》课程教学讲义（下）12-7 位移电流

麦克斯韦电磁理论 一、电流密度 方向：沿电流方向 电流密度了 大小：= 0- SI:A/m2 dl jdS jdS cos0=jds dl =j.ds 1=∫d=jas 电流强度等于电流密度的通量 二、位移电流 Φn=D.as D,C1m2；Φp,C 曲面固定，电场随时间变化 dp= 0.硅面国定 aD .d dt :Cm)=m，位移电流密度：-0 aD t :Cls=A, 位移电流：ID= dΦp dt dt 1n=jo·d D=E,j。= aD = E,真空中，。= OD aE 位移电流的本质是变化的电场 三、静电场和稳恒磁场 静电场， fEo.d=0 稳恒磁场， f.d5=0 fi0.d=∑1 内 四、两个假说 1、涡旋电场假说：变化的磁场产生祸旋电场 f2.i=-地=- a dt Js ot .d6 涡旋电力线的环绕方向 aB/at 与aB/1满足左手定则 E2) aB/at .ds=0 1

1 麦克斯韦电磁理论 一、电流密度 电流密度      dS dI j j 大小：  方向：沿电流方向 SI： 2 A/ m dI jdS jdS j dS      n cos n  j dI j dS          S I dI j dS   S 电流强度等于电流密度的通量 二、位移电流 D      S D D dS   S D ， ； ，  2 C / m D C 曲面固定，电场随时间变化         S S D dS t D D dS dt d dt d    曲面固定 ： ， 位移电流密度： t D    2 2 C（/ m s） A/ m t D jD      ： ， 位移电流： dt dD C /s  A dt d I D D   I j dS S D D      D E ， = ，真空中， =     t D jD      t E     t D jD      t E    0  位移电流的本质是变化的电场 三、静电场和稳恒磁场 静电场， S D  dS  q f 内 （ ）   1    L E dl 0 1   （ ） 稳恒磁场，    S B dS 0 1   （ ） L H  dl  I 内 传 （ ）   1 四、两个假说 1、涡旋电场假说：变化的磁场产生涡旋电场 dS t B dt d E dl L S m                （2） 涡旋电力线的环绕方向 B / t  与B / t 满足左手定则  (2) E  B / t     S D dS 0 2   （ ）  dS dI j I dS (2) E 

2、位移电流假说 .dS dt i2线的环绕方向 aD/at 与aD/ar满足右手定则 aD/at Ba.d5=0 I(2 变化的电场产生磁场 电荷→电场 ↓个 电磁场 运动电荷→磁场 五、麦克斯韦方程组的积分形式 静电场：0、D0, 传导电流的磁场：B、四 涡旋电场：E2)、D2, 位移电流的磁场：B2、2 D=D0+D2,E-E0+E2,B=B0+B2),i=i四+i2) fD-a=5D.S+fD2.a=∑9 电场的高斯定理 E.di=f.Eo.di+fEe).di=_d dt 法拉第电磁感应定律 fB.否=重Bo.aS+fB2.a=0 磁场的高斯定理 0山=fi+f扣i-2,+0-⅓ 全电流安培环路定律 ∑：+。：全电流，不包括磁化电流 p-d- fE.ai- dt 麦克斯韦方程组 f8.心=0 -4,+0 d +电导率 D=sE,B=uH,j=o 洛仑兹力公式F=gE+g严×B 变化的电磁场在空间传播一电磁波 真空中电磁波的波速c= 一≈3×103m/s=真空光速 EoMo 光是电磁波，（麦克斯韦1865)，1888，赫兹实验

2 2、位移电流假说      L D D dt d H dl I   （2）      S dS t D   线的环绕方向 (2) H  D / t  与D / t 满足右手定则  (2) H  D / t     S B dS 0 2   （ ） (2) H  变化的电场产生磁场 电荷电场  电磁场 运动电荷磁场 五、麦克斯韦方程组的积分形式 静电场： E (1) 、 ， 传导电流的磁场： 、  (1) D  (1) B  (1) H  涡旋电场： E (2) 、 ， 位移电流的磁场： 、  (2) D  (2) B  (2) H  D D (1) D (2) ， ， ，      (1) (2) E E E      (1) (2) B B B      (1) (2) H H H         S       f S S D dS D dS D dS q 内 （ ）       1 (2) 电场的高斯定理            L m L L dt d E dl E dl E dl       （1） (2) 法拉第电磁感应定律          S S S B dS B dS B dS 0 1 (2)       （ ） 磁场的高斯定理 全 内 传 （ ） I dt d H dl H dl H dl I D L L L                    1 (2) 全电流安培环路定律 I  I  ID ：全电流，不包括磁化电流 内 全 传     内 f S D dS q   dt d E dl m L          0 S B dS   dt d H dl I D L       内 传   D E ， ，     B H     j E     洛仑兹力公式 F qE qV B        变化的电磁场在空间传播电磁波 真空中电磁波的波速c 3 10 m/s =真空光速 1 8 0 0      光是电磁波，（麦克斯韦 1865），1888，赫兹实验 麦克斯韦方程组 电导率

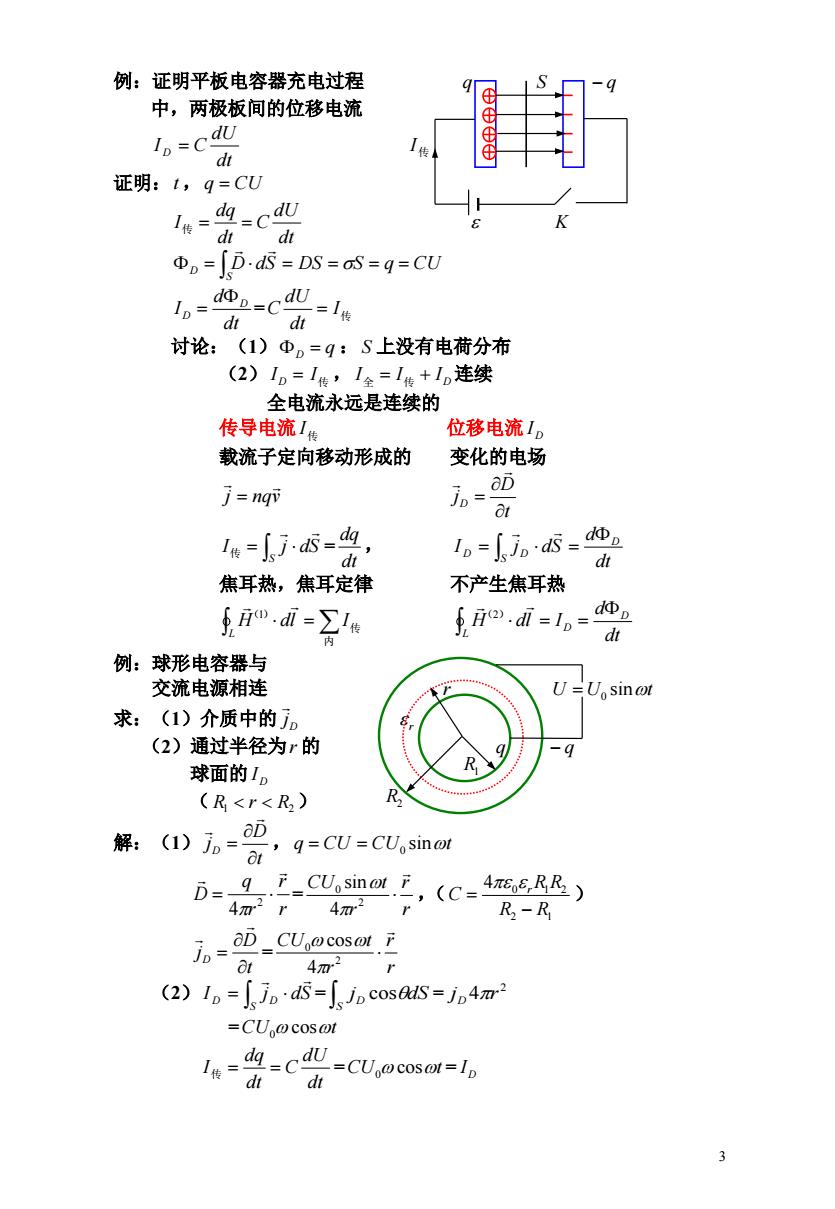
例：证明平板电容器充电过程 中，两极板间的位移电流 1-c 证明：t,q=CU 1%-=c0 Φn=∫Dds=DS=S=g=CU 1。-=C dt dt 二1传 讨论：(1)Φ。=q:S上没有电荷分布 (2)1o=1传，1全=1传+1连续 全电流永远是连续的 传导电流1传 位移电流I。 载流子定向移动形成的 变化的电场 j=nqv a-0 at e=j5=, 1。=jn5=地o dt 焦耳热，焦耳定律 不产生焦耳热 ,di=罗e fF.di=1p= op dt 例：球形电容器与 交流电源相连 U=Usin @t 求： (1)介质中的j。 (2)通过半径为r的 -9 球面的I。 (R<r<R2) 解： (1)。=0 ’9=CU=CU,sino D=gCUasinoo.(C=4m,R) 4m2 R-R jn=eD-CUocosou F 4m2 (2)I=jods=f jpcos@s=j42 =CU@cos@t -dq=CdU-CUcO-Ip 1传=d

3 例：证明平板电容器充电过程 q S  q 中，两极板间的位移电流 dt dU I D  C I传 证明：t ，q  CU dt dU C dt dq I传    K     S D D dS    DS  S  q  CU = dt d I D D   I传 dt dU C  讨论：（1）D  q ： S 上没有电荷分布 （2） ID  I传 ， I全  I传  ID 连续 全电流永远是连续的 传导电流 I传 位移电流 D I 载流子定向移动形成的 变化的电场 j nqv    t D jD      = ，    S I j dS   传 dt dq I j dS S D D      dt dD  焦耳热，焦耳定律 不产生焦耳热 L H  dl  I 内 传 （ ）   1      L D D dt d H dl I   （2） 例：球形电容器与 交流电源相连 r U U sint  0 求：（1）介质中的 D j r  （2）通过半径为r 的 q  q 球面的 D I （ R1  r  R2 ） 解：（1） ，t D jD      q CU CU sint   0 = ，（ ） r r r q D     2 4 r r r CU t   2 0 4 sin   2 1 4 0 1 2 R R R R C r    = t D jD      r r r CU t   2 0 4 cos    （2） I j dS = = S D D      j dS S D cos  2 j 4 r D  =CU  cost 0 = = dt dU C dt dq I传   CU  cost 0 D I R1 R2

例：圆片平板电容器 q=go sinot 求：(1)板间j。、1o (2)r(<R)处的 H、B、w &(1)b=,D=a=9-96sin S TR2,jD= D goo cosot Ot R2 Ip=S jpdS-Ssjp cos@dS-jpS-qoocosot (2)重H.d=1o，H2m=jom2-9%0 cosl R2 27R2F,B=HoH=Hoqoocosot H=9o0cosot 2πR2 w=}D.E+B月=1D+l 2624H (sincos) 1 4 例：+q以速率V朝O点运动 1时刻+g与O点相距x 求：(1)通过圆面的I。 (2)圆周上的B +g 解：(1)Φn=D.aS=DcosadS - =20dy 291x R) 1n=e=m2在=1 x2+Rn,(W=-) dt dx dt9p2 dt a)f用d-=,H2=re (x2+R2)32 H= gVR MoqVR 4元x2+R)p’B=oH=4知2 rR sinaR 日=总旷2，日-会：运动电有的磁场」 4πr2 4

4 例：圆片平板电容器 q  q q q sint  0 R r 求：（1）板间 jD 、 D I （2）r( R) 处的 H 、 B 、 w 解：（1） ， ， = t D jD    2 0 sin R q t S q D       t D jD    2 0 cos R q t    I j dS = = = S D D      j dS S D cos  jDS q  cost 0 （2） ， =    L D H dl I   2 H 2 r j r   D 2 2 0 cos r R q t     r ， R q t H 2 0 2 cos     r R q t B H 2 0 0 0 2 cos        2 0 0 2 2 1 2 1 2 1 2 1 H D w D E B H             = cos ) 4 1 (sin 2 2 2 2 0 0 2 4 0 2 2 0 t r t R q         例： q以速率V 朝O点运动 R D  t 时刻 q与O点相距 x r  求：（1）通过圆面的 D I  （2）圆周上的 B   q V x 解：（1） =     S D D dS   S DcosdS =    S ydy x y x x y q   2 4 ( ) 2 2 2 2 = =   R x y ydy qx 0 2 2 3 / 2 2 ( ) 1 0 ) 1 ( 2 1 2 2 R x y qx   = (1 ) 2 1 2 2 x R x q    ，( )     dt dx dx d dt d I D D D 2 2 3 / 2 2 2 ( ) 1 x R R qV  dt dx V   （2）    ， L D H dl I   H 2R  2 2 3 / 2 2 2 ( ) 1 x R R qV  2 2 3 / 2 ， 4 (x R ) qVR H    2 2 3 / 2 0 0 4 (x R ) qVR B H       ，r R sin  2 2 r  x  R 0 2 ， ：运动电荷的磁场！ sin 4 r qV B     3 0 4 r qV r B        H    n  H  dy O y

例：电容器充电过程中 (1)Hdi>旺d (2)ǖdi=盟d (3)id<短d团 00. (4)f狂.di=0 例：在无自由电荷与传导电流的空间区域， 变化的电磁场遵循的规律？ D.ds=?,sE.di=?,$B.d5=?,f.di=? 0-8=0,Ei=-”,B-函=0，l=0

5 例：电容器充电过程中 （1）      L1 L2 H dl H dl     L1 （2）      L1 L2 H dl H dl     （3）      L1 L2 H dl H dl     L2 （4） 0 1   L H dl   例：在无自由电荷与传导电流的空间区域， 变化的电磁场遵循的规律？    ?， ， ， S D dS     ? L E dl     ? S B dS     ? L H dl      0 ， ， ， S D dS   dt d E dl m L          0 S B dS   dt d H dl D L      