11一6磁场对运动电荷的作用 一、洛仑兹力 安培力:dF=ld×B B Idi qvdN dF =qv x BdN @④ 洛仑兹力:F=d匠 =xB F=gvBsin0,0:下与B的夹角 F⊥Π(,B),q>0,F指向下×B的方向 q0 B 9<0 B B F F1下,功率P=F.下=0,洛仑兹力对电荷不作功 二、带电粒子在电磁场中的运动 m,q,(E,B),F=qE+q下×B:洛仑兹力 qgE+qp×B=ma= 27 d 动力学方程 例:均匀磁场,带电粒子初速度LB BX X v2 F=qgi×B,F=qB=m gB 周期T=2R-2mm与v无关 gB 例:均匀磁场,带电粒子初速度下与B夹角日 1
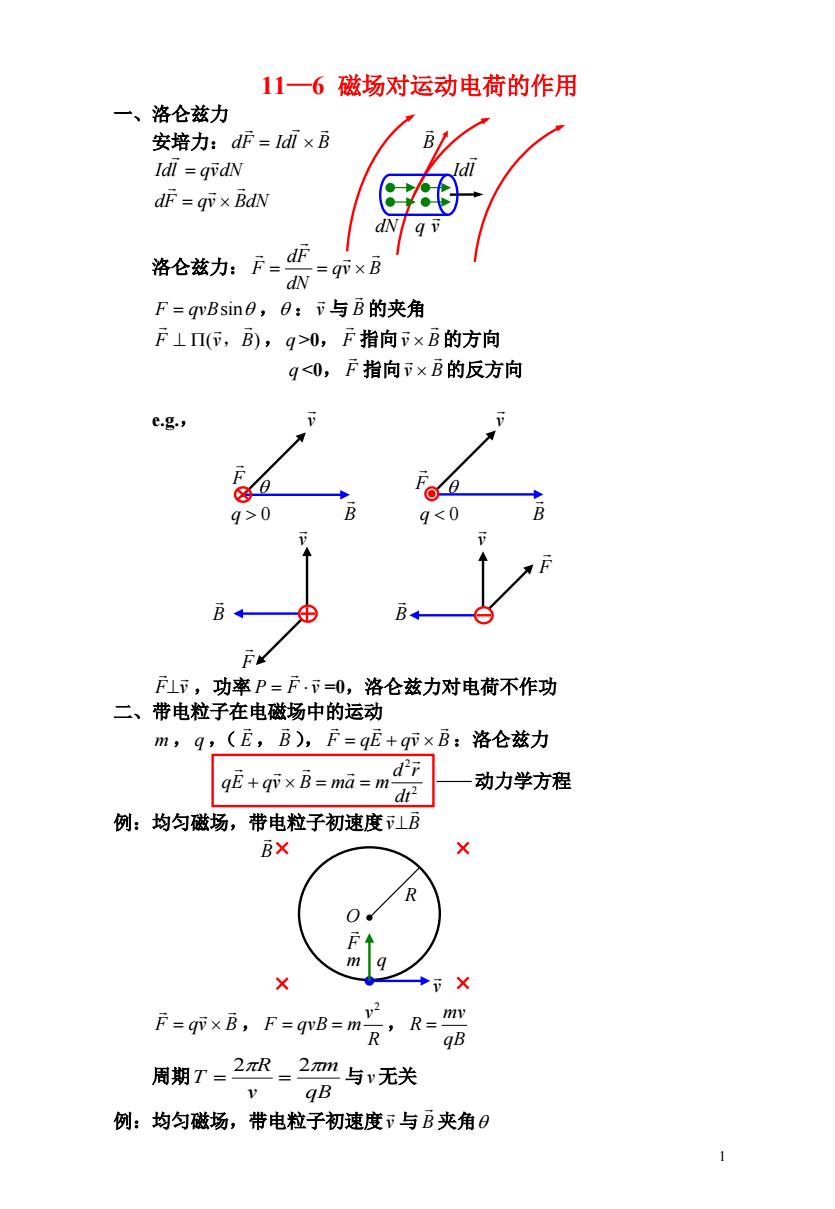
1 11—6 磁场对运动电荷的作用 一、洛仑兹力 安培力:dF Idl B B Idl qvdN Idl dF qv BdN dN q v 洛仑兹力: qv B dN dF F F qvBsin , :v 与 的夹角 B F (v B) , >0, 指向 的方向 , q F v B q <0, F 指向 的反方向 v B e.g., v v q 0 B q 0 B v v F B B F F v ,功率 =0,洛仑兹力对电荷不作功 P F v 二、带电粒子在电磁场中的运动 m ,q ,( E , ), :洛仑兹力 B F qE qv B 2 动力学方程 2 dt d r qE qv B ma m 例:均匀磁场,带电粒子初速度v B B R O F m q v F qv B , , R v F qvB m 2 qB mv R 周期 与 无关 qB m v R T 2 2 v 例:均匀磁场,带电粒子初速度v 与 夹角 B F F

m,g vu v=vcose,v =vsine,F=qvBsine=qBv R=mm=mwsn0,螺距h=,T=cos02m gB gB gB 质谱仪、速度选择器、回旋加速器、电子射线管、磁透镜 磁聚焦、磁约束 三、霍尔效应 ua:霍耳电压 ty b b:磁场方向的边长 L-风号 R,:霍耳系数 导电材料 R与1、B、b无关 BX 土土十土土土 仅与导电材料种类有关 n 9>0: 9>0 下与同方向 Fn=qB,方向个 X E:霍耳电场,方向↓,F=qE1,方向↓ 开始,E,较弱,F0时相反× 2
2 v v B // v m ,q // v h v// v cos ,v vsin , F qvBsin = qB v ,螺距 qB mv qB mv R sin qB m h v T v 2 cos // 质谱仪、速度选择器、回旋加速器、电子射线管、磁透镜 磁聚焦、磁约束 三、霍尔效应 :霍耳电压 uH B b IB uH c b :磁场方向的边长 a I b IB uH RH RH :霍耳系数 导电材料 与 、 、 无关 RH I B b B 仅与导电材料种类有关 n Fm q 0: q 0 v I v 与 同方向 I Fm qvB ,方向 EH :霍耳电场,方向 , Fe qEH ,方向 开始, EH 较弱, Fe Fm t , EH , Fe ,直到, Fe Fm ,稳定状态 Fe Fm ,qEH qvB , EH vB uH EH a vBa (1) I nqvS nqvab (2) , ,令 , nqb B I uH b IB nq uH 1 nq RH 1 b IB uH RH q 0 B I 、 B 方向不变 Fm v 与 反方向 I q 0 I Fm qv B ,方向 EH 、uH 与q 0时相反 b UH Fe v
利用霍耳效应可以判断载流子带电的符号 金属材料:载流子:电子 n型半导体:载流子:电子 p型半导体:载流子:空穴 还可测量n、I、B 例:判断载流子带什么电? BX 1 412>0 例: B O→ m、ep (1) (2) 求:an和a 解:(1)an=0,a,=eE/m (2)an=V(eE)2+(evB)2/m,a,=0
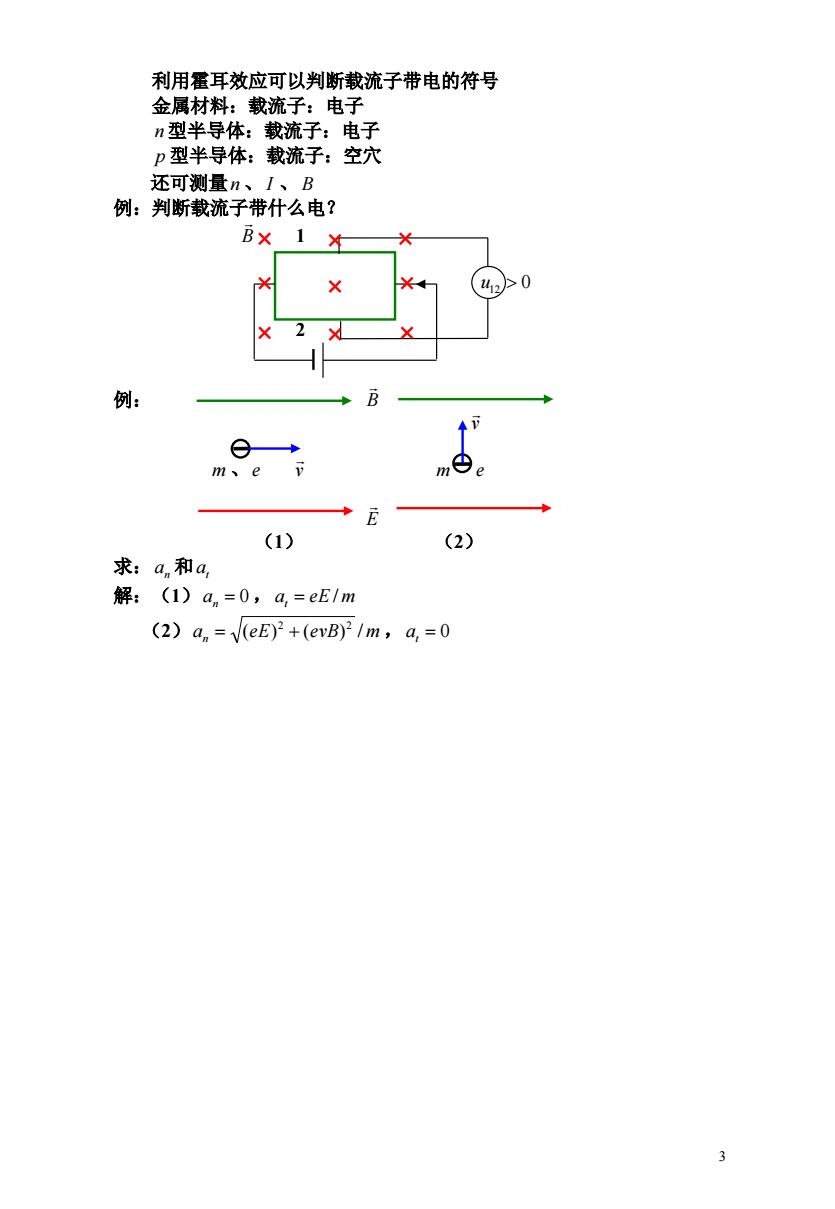
3 利用霍耳效应可以判断载流子带电的符号 金属材料:载流子:电子 n 型半导体:载流子:电子 p 型半导体:载流子:空穴 还可测量n 、 I 、 B 例:判断载流子带什么电? B 1 u12 0 2 例: B v m 、e v m e E (1) (2) 求:an 和at 解:(1)an 0 ,at eE / m (2)an (eE) 2 (evB) 2 / m ,at 0