
12一5互感 一、互感现象及其规律 1,激发的磁场穿过2的磁通量 Φ21cI1,Φ21=M21 L,激发的磁场穿过1的磁通量 D12cI2,Φ12=M22 M21:1对2的互感系数,M2:2对1的互感系数 M21三M2=M:互感系数,SI:H M:形状、大小、面积、匝数、磁介质、相对位置有关 Φ21=ML1,D12=M2 推论:if,1=12,Φ2=①2162 61=-@=-M d t 2s、 Φ2=-ML 621、62互感电动势 两线圈磁场相互加强时,电流的流入端称为两线圈的同名端 电流由同名端流入时,互感电动势正方向与自感电动势相同 两线圈磁场相互削弱时,电流的流入端称为两线圈的异名端 电流由异名端流入时,互感电动势正方向与自感电动势相反 8L2 二、M的计算 M--,M=-= dt 例:两个共轴螺线管,n1,nh2,半径R,4,2>R 】 (1)证明:M21=M2(2)M与L,、L2的关系 解:(1)B=m,l1,B2=m2l2 =N,B.S=nl:imlk,Ma=a=mlR 1
1 12—5 互感 一、互感现象及其规律 1 2 I 1 激发的磁场穿过 2 的磁通量 21 I 1 , 21 21 1 M I 激发的磁场穿过 1 的磁通量 2 I 1I 2 I 12 I 2 , 12 12 2 M I M21 :1 对 2 的互感系数, M12 :2 对 1 的互感系数 M21 M12 = M :互感系数,SI:H M :形状、大小、面积、匝数、磁介质、相对位置有关 21 MI 1 , 12 M 2 I 推论:if, I 1 I 2 ,12 21 12 1 21 2 dt dI M dt d 21 1 21 L1 L2 dt dI M dt d 12 2 12 I 1 I 2 21 、 12 互感电动势 两线圈磁场相互加强时,电流的流入端称为两线圈的同名端 电流由同名端流入时,互感电动势正方向与自感电动势相同 两线圈磁场相互削弱时,电流的流入端称为两线圈的异名端 电流由异名端流入时,互感电动势正方向与自感电动势相反 1, 2 12 21 L1 L2 1I 2 I 二、 M 的计算 ,2 12 1 21 I I M /( ) /( ) 2 12 1 21 dt dI dt dI M 例:两个共轴螺线管,n1 l1 ,n2 l2 ,半径 R ,l1 ,l2 R 1I 2 I (1)证明: M21 = M12 (2) M 与 L1 、 L2 的关系 解:(1) B1 n1I 1 , 2 2 2 B n I 21 N2B1S n2 l2n1I 1R 2 , 2 1 2 2 1 21 21 n n l R I M 2 l

中e=NB,S=mhml,aR',M:=号 _D2=unnlaR M21=M2=M=n,n2l2πR2 (2)L=4mlR2,L2=4m2πR √LL2=m,n2Vh2R2 六意臣授g 一般,M=kVLL2,常数0≤k≤1:耦合系数 由两个线圈的相对位置决定 讨论: (1)无漏磁耦合,k=1,M=√L 如果,L=L2=L,M=L (2)松耦合,两线圈相距很远 或垂直摆放 k≈0,M≈0 0 例:线圈串联 解:(1)顺串联(磁场相互加强) EL=EL1+812+8L2+621 L.M =-Ldt dlM dI一M-L2 dt dt dl 81 =-(L+L2+2M) L=,-=L+L,+2M 2 d (2)反串联(磁场相互削弱) 8L=81-812+8L2-82l =di da一itM dt =-(L1+L2-2M) dl 812 21 =M0-+4-2w 讨论:(1)顺串联还是反串联看磁场是相互加强还是削弱 (2)顺串联L=L1+L2+2k√LL2 反串联L=L1+L2-2kVLL2 无漏磁耦合k=1 顺串联L=L+L2+2V√LL2 2
2 12 N1 B2S n1 l2n2I 2R 2 , 2 1 2 2 2 12 12 n n l R I M 2 M21 M12 M n1n2 l2R (2) L1 n1 2 l1R 2 , 2 2 2 L2 n2 l R 2 L1L2 n1n2 l1 l2R ,1 2 1 2 2 1 2 l l l l l L L M 1 2 1 2 L L l l M 一般, M k L1L2 ,常数0 k 1:耦合系数 由两个线圈的相对位置决定 讨论: (1)无漏磁耦合,k 1, M L1L2 如果, L1 L2 L , M L (2)松耦合,两线圈相距很远 或垂直摆放 k 0, M 0 例:线圈串联 解:(1)顺串联(磁场相互加强) 1 12 2 21 L L L L1 M L2 = dt dI M dt dI L dt dI M dt dI L1 2 = dt dI (L L 2M ) 1 2 /( ) 1 2 3 4 dt dI L L L1 L2 2M (2)反串联(磁场相互削弱) 1 12 2 21 L L L L1 M L2 = dt dI M dt dI L dt dI M dt dI L1 2 = dt dI (L L 2M ) 1 2 /( ) 1 2 4 dt dI L L L1 L2 2M 讨论:(1)顺串联还是反串联看磁场是相互加强还是削弱 (2)顺串联 L = 1 2 2 L1L2 L L k 反串联 L = 1 2 2 L1L2 L L k 无漏磁耦合k 1 顺串联 L = L1 L2 2 L1L2 12 L1 21 L2 12 L1 21 L2 3 I I
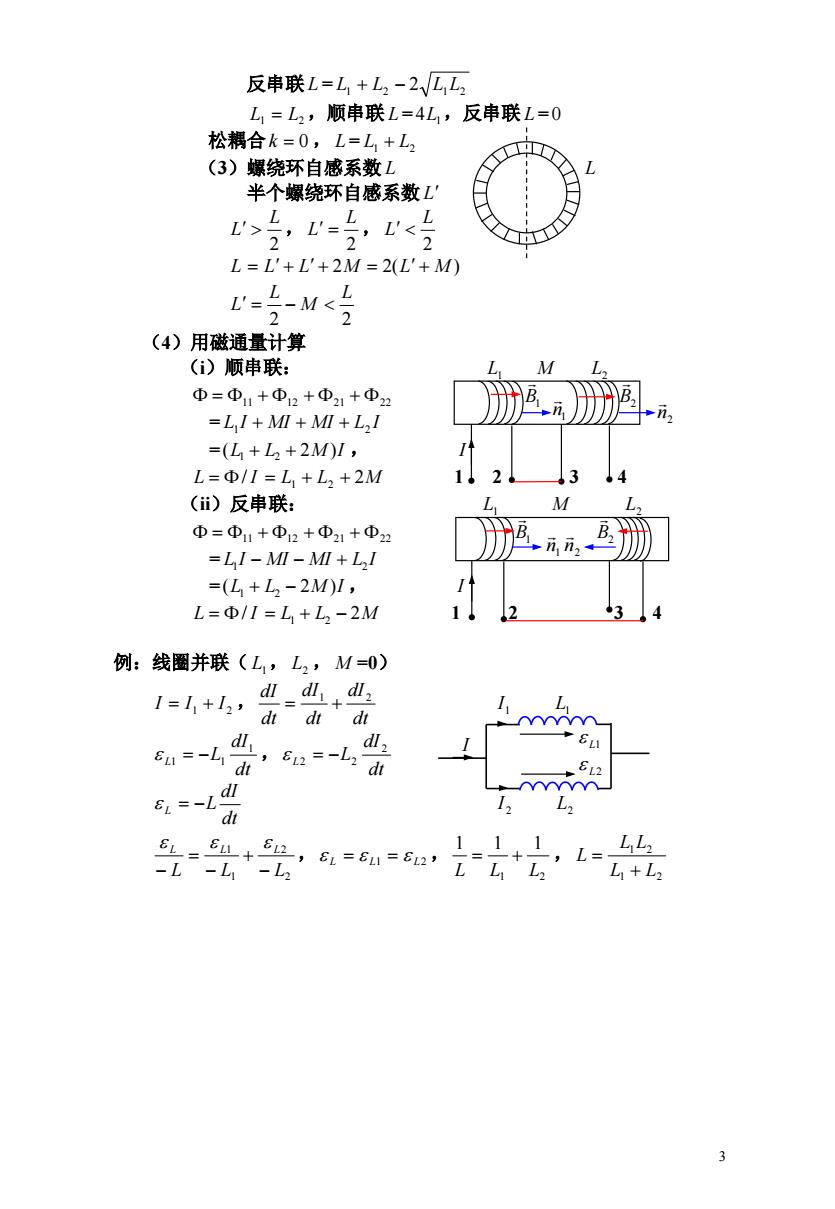
反串联L=L1+L2-2VL L1=L2,顺串联L=4L1,反串联L=0 松耦合k=0,L=L+L2 (3)螺绕环自感系数L 半个螺绕环自感系数L L=L'+L'+2M=2(L'+M) r-2M< (4)用磁通量计算 (i)顺串联: M ④=Φ1+Φ12+Φ21+Φ22 =LI+MI+MI+L,I =(L+L2+2M1, L=Φ/I=L,+L,+2M (ii)反串联: Φ=D11+D12+Φ21+Φ2 =LI-MI-MI+LI =(L+L2-2M1, L=Φ/1=L+L2-2M 例:线圈并联(L,L2,M=0) 1=11+12, dldid dt dtdt 8n=-山d’ 5ua=-1 di dl2 6L2 d 8L=-L 1 dt =4+62,6L=6=62,i=,+,L=, -L-L1-L2 L1+L2 3
3 反串联 L = L1 L2 2 L1L2 L1 L2 ,顺串联 L = 4L1 ,反串联 L =0 松耦合k 0 , L = L1 L2 (3)螺绕环自感系数 L L 半个螺绕环自感系数 L , , 2 L L 2 L L 2 L L L L L 2M 2(L M ) 2 2 L M L L (4)用磁通量计算 (i)顺串联: L1 M L2 11 12 21 22 = L I MI MI L I 1 2 =(L L 2M )I , 1 2 I L / I L1 L2 2M 1 2 3 4 (ii)反串联: L1 M L2 11 12 21 22 = L I MI MI L I 1 2 =(L L 2M )I , 1 2 I L / I L1 L2 2M 1 2 3 4 例:线圈并联( L1 , L2 , M =0) , 1 2 I I I dt dI dt dI dt dI 1 2 1 I L1 , dt dI L L 1 1 1 dt dI L L 2 2 2 dt dI L L 2 I L2 , , , 2 2 1 1 L L L L L L L L1 L2 1 2 1 1 1 L L L 1 2 1 2 L L L L L L1 L2 B2 B1 B2 B1B1 2 n n1 2 n n1 I
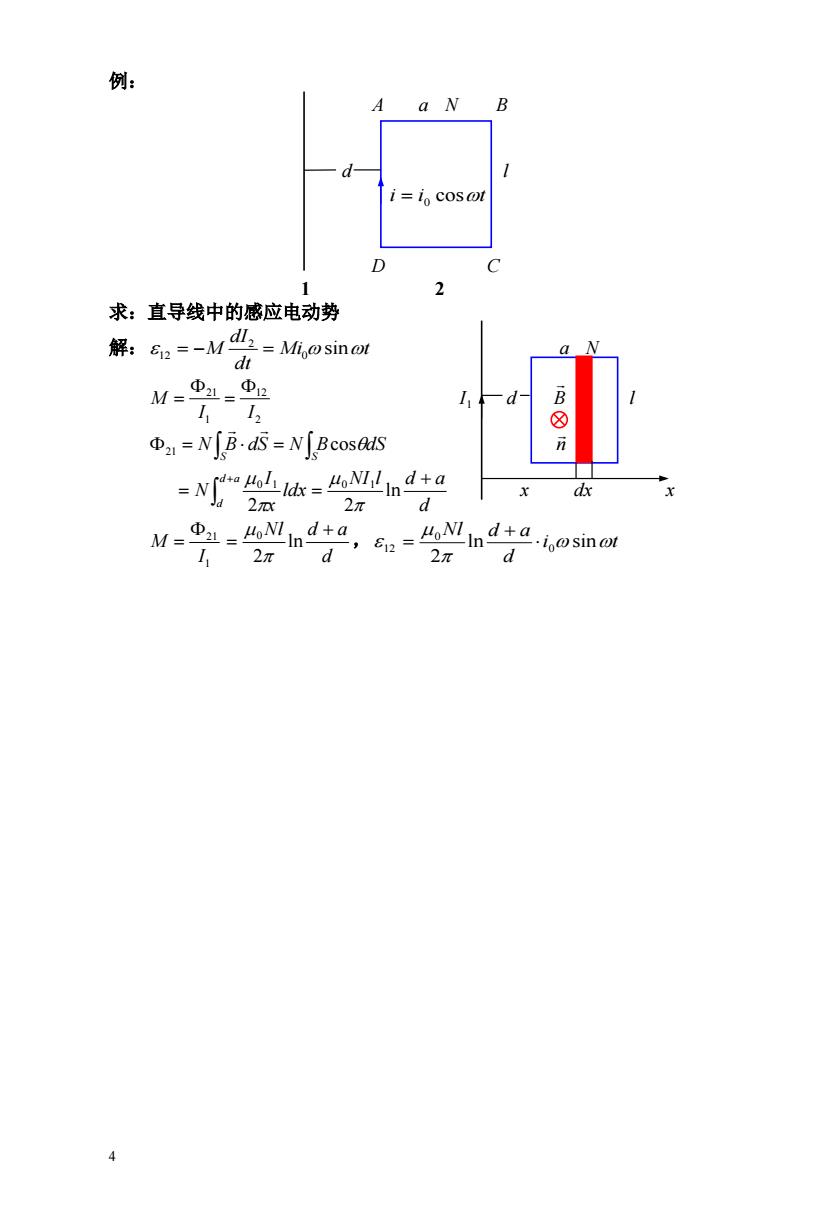
例: Aa N B d i=io cosot D 2 求:直导线中的感应电动势 解: e=-M业=Mi.psinot Q dt M=1-2 112 ④1=NB.s=N[Bcose6S B⑧n =N0=n牛 dx 2 2元 d M=2 Ind+a =HoNI in,=么 2π d isinot 4
4 例: A a N B d l i i cost 0 D C 1 2 求:直导线中的感应电动势 解: Mi t dt dI M 0sin 2 12 a N 2 12 1 21 I I M 1 I d B l S S 21 N B dS N BcosdS n d NI l d a ldx x I N d a d ln 2 2 0 1 0 1 x dx x , 1 21 I M d Nl d a ln 2 0 i t d Nl d a ln sin 2 0 0 12