西安电子科技大学：《大学物理》课程教学讲义（下）12-4 自感

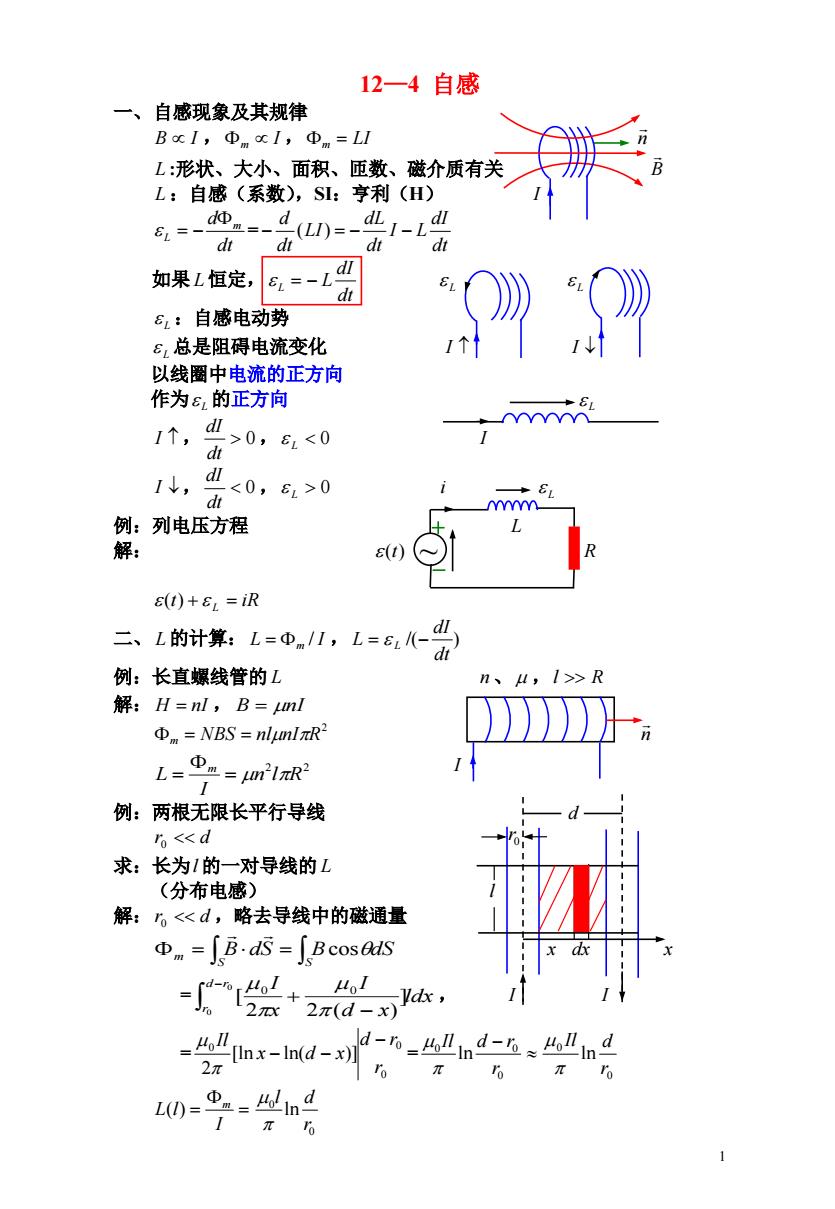
12一4自感 一、自感现象及其规律 BcI,ΦmcI,Φm=LI L:形状、大小、面积、匝数、磁介质有关 L:自感（系数），SI:亨利(H) ,=--dn=-dL1- dt dt dt dt 如果L恒定， 6 =-1dI d 6：自感电动势 8,总是阻碍电流变化 以线圈中电流的正方向 作为8，的正方向 dⅢ 1↑，4>0，,0 dt Y 例：列电压方程 解： s(t E(1)+81=iR 二、L的计算：L=Φ1，L=6(- dt 例：长直螺线管的L n、4,1>R 解：H=nl,B=ml Φm=NBS=nlunlπR2 1=9=m 例：两根无限长平行导线 <<d 求：长为1的一对导线的L (分布电感) 解：。<d,略去导线中的磁通量 Φm=[B.ds=[Bcos@S dx -编+2 2π(d-x) -x-nd-6 )d-n_4ind-h≈ind 2π π L(0= π6

1 12—4 自感 一、自感现象及其规律 B  I ， I ， m  LI m  n  L :形状、大小、面积、匝数、磁介质有关 B  L ：自感（系数），SI：亨利（H） I = dt d m L     dt dI I L dt dL LI dt d  ( )    如果 L 恒定，  L  dt dI  L L  L  ：自感电动势 L  总是阻碍电流变化 L  I  I  以线圈中电流的正方向 作为 的正方向 L  L  I ，  0 ， dt dI  L  0 I I ，  0 ， dt dI  L  0 i L  例：列电压方程 L 解：  (t) R  (t)   L  iR 二、 L 的计算： L  m / I ， /( ) dt dI L   L  例：长直螺线管的 L n 、  ，l  R 解： H  nI ， B  nI 2 m  NBS  nlnIR n  2 2 n l R I L m      例：两根无限长平行导线 d r0  d 求：长为l 的一对导线的 L （分布电感） l 解：r0  d ，略去导线中的磁通量       S S m B dS BcosdS   x dx x = ldx ， d x I x d r I r    0 0 ] 2 2 ( ) [ 0 0     I I = = 0 0 0 [ln ln( )] 2 r d r x d x Il      0 0 0 ln r Il d  r   0 0 ln r Il d       I L l m ( ) 0 0 ln r l d   0r ~ I

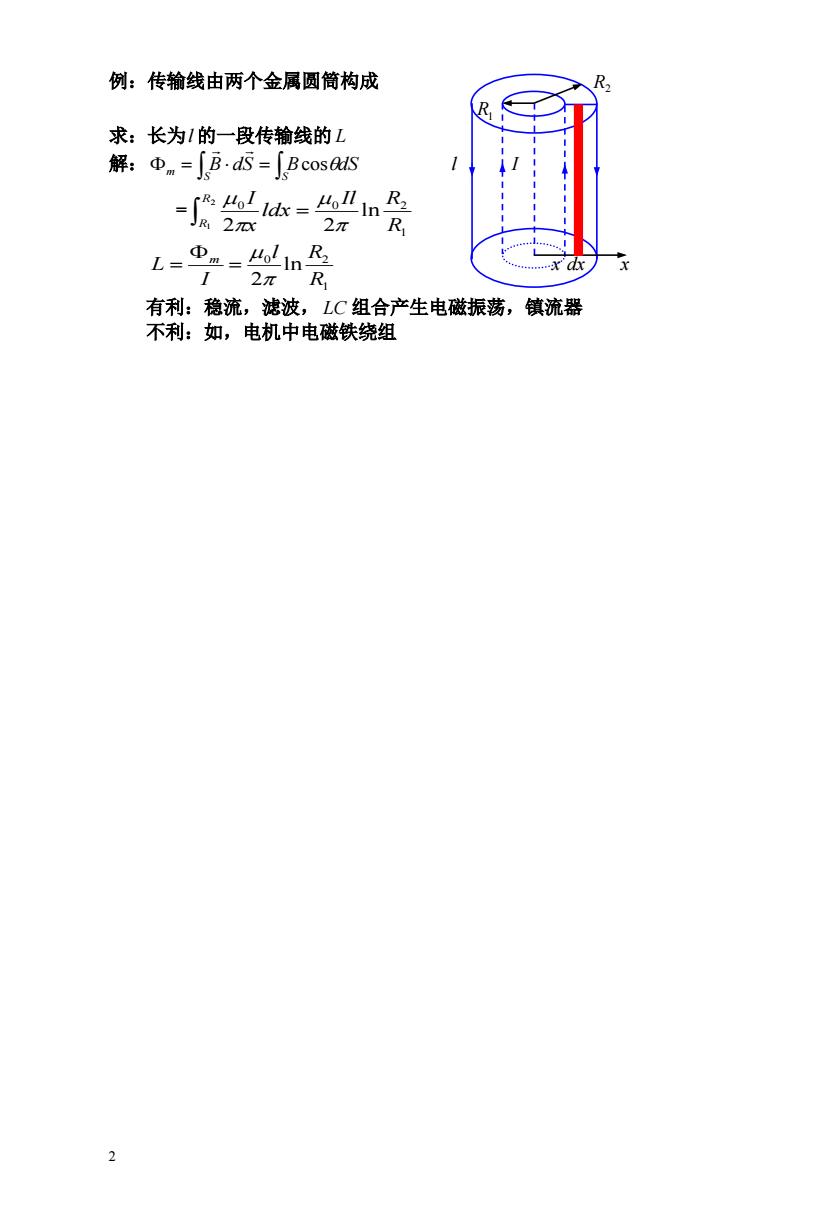
例：传输线由两个金属圆筒构成 求：长为1的一段传输线的L 解：Φm=∫B.dS=BcosaS =收= 2元 R 、R2 Xd次 有利：稳流，滤波，LC组合产生电磁振荡，镇流器 不利：如，电机中电磁铁绕组 2

2 例：传输线由两个金属圆筒构成 R2 R1 求：长为l 的一段传输线的 L 解：       S S m B dS BcosdS   l I = 1 0 0 2 ln 2 2 2 1 R Il R ldx x R I R       1 0 2 ln 2 R l R I L m      x dx x 有利：稳流，滤波， LC 组合产生电磁振荡，镇流器 不利：如，电机中电磁铁绕组