
第4节理想气体绝热过程 绝热过程:0=0,Q=0 一、准静态绝热过程 do=dE+=0,dE vCdT,dA=Pdv VCydT+Pdv=0,dT=-P dv PV VRT,PdV +VdP vRdT Pdv+VdP=R (P dr)Rpdv C (1+R )PdV+Vdp=0,yPdV +Vdp=0 ,d业+ap p=0,yInv+Inp= PV”=e=C一绝热过程方程(泊松方程) PVT =PVY PV?=c G=PVT PVVT-I=VRTVI-,TVY-1=C C=PVr=prpl-rVr=(vRTy pl-7,pr-T-7=C PVY=c TVI-I=C pr-T-7=C3 例:狄塞尔内燃机气缸中的空气,在压缩前温度为320K,压强 为1.013×10Pa,假定空气突然被压缩到原来体积的1/16.9 求:压缩终了时气缸内空气的温度和压强(空气的y=1.4) 解:看作绝热压缩,压缩前(P,V,T),压缩后(,'2,T) T=1,五=I(y=320x16.941=992K 1.013x10653.05x10Pa pwi=a,P= 绝热 等温过程,PV=RT=C M(P,V) P= 等温 V c'I P VV+△V1 dp P=nkT,等温膨胀过程,V个,n↓,T不变,P↓ 绝热膨胀过程,V个,n↓,T↓,P八 1
1 第 4 节 理想气体绝热过程 绝热过程:dQ 0 ,Q 0 一、准静态绝热过程 dQ dE dA =0,dE CV dT ,dA PdV CV dT PdV 0, dV C P dT V PV RT , PdV VdP RdT PdV VdP R ( dV )= C P V PdV C R V (1 )PdV VdP 0, C R V PdV VdP 0 0 , P dP V dV lnV ln P c PV e c c1 绝热过程方程(泊松方程) 1 1 2 2 1 PV PV PV c c1 PV PVV 1 RTV 1 , 2 1 TV c c1 PV P P 1 V (RT) P 1 , 3 1 P T c 1 PV c 2 1 TV c 3 1 P T c 例:狄塞尔内燃机气缸中的空气,在压缩前温度为 320K,压强 为1.01310 5Pa ,假定空气突然被压缩到原来体积的1/16.9 求:压缩终了时气缸内空气的温度和压强(空气的 1.4) 解:看作绝热压缩,压缩前(P1 ,V1 ,T1),压缩后( , , ) P2 V2 T2 ,1 2 2 1 1 1 TV T V K V V T T ( ) 320 16.9 992 1 1.4 1 2 1 2 1 P1V1 P2V2 , Pa V V P P 5 1.4 5 2 1 2 1( ) 1.01310 16.9 53.0510 PV c1 , 绝热 V c P 1 等温过程, PV RT c 等温 V c P V P V V c V c dV dP T 1 ( ) 2 V V V V ,V P V V c V c dV dP Q 1 ( ) 1 1 1 0 ( )Q0 dV dP T dV dP ( ) P nkT ,等温膨胀过程,V ,n ,T 不变, P 绝热膨胀过程,V ,n , T , P P P P M(P,V)

方法1、Q=0 △E=。R(T2-T) P I(P,V,T) =P5-P) Ⅲ(2,'2,T2) A=-△E =-RT2-TI), ' 2(-) 方法2、Q=0 A-A y-1 PVT=PV=c A=1(P4-P) y-1 △E=-A 二、绝热自由膨胀 挡板 PVT 真空 PVT 绝热刚性容器 Q=0,A=0,△E=0,膨胀前后及中间过程内能不变 对真实气体也成立 理想气体,AE=0,E=E,2RT=R☑,T=了 P彤=R,月5=R,P=P,如果乃=2斯,乃= 注意:(1)中间过程不是平衡态,理想气体状态方程不成立 (2)始末状态温度相等,但不是等温过程 (3)是绝热过程,但不是准静态的 泊松方程不成立,PV≠P以,P=' 2
2 方法 1、Q 0 ( ) 2 R T2 T1 i E P = ( ) 2 P2V2 P1V1 i A E = ( ) , 2 R T2 T1 i V1 V2 V = ( ) 2 P1V1 P2V2 i 方法 2、Q 0 1 1 1 1 2 1 2 1 2 1 V V V c dV V c A PdV V V V V = ( ) 1 ( ) 1 1 2 1 1 1 1 1 1 2 1 V V c V V c 1 1 2 2 1 PV PV c ( ) 1 1 A P1V1 P2V2 E A ? 1 1 2 i 二、绝热自由膨胀 挡板 真空 P1V1T1 P2V2T2 绝热刚性容器 Q 0, A 0 ,E 0,膨胀前后及中间过程内能不变 对真实气体也成立 理想气体,E 0, E1 E2 , 1 2 , 2 2 RT i RT i T1 T2 P1V1 RT1 , P2V2 RT2 , P1V1 = P2V2 ,如果V2 2V1 , 2 1 2 1 P P 注意:(1)中间过程不是平衡态,理想气体状态方程不成立 (2)始末状态温度相等,但不是等温过程 (3)是绝热过程,但不是准静态的 泊松方程不成立, , = P1V1 P2V2 P1V1 P2V2 ( , , ) P1 V1 T1 ( , , ) P2 V2 T2
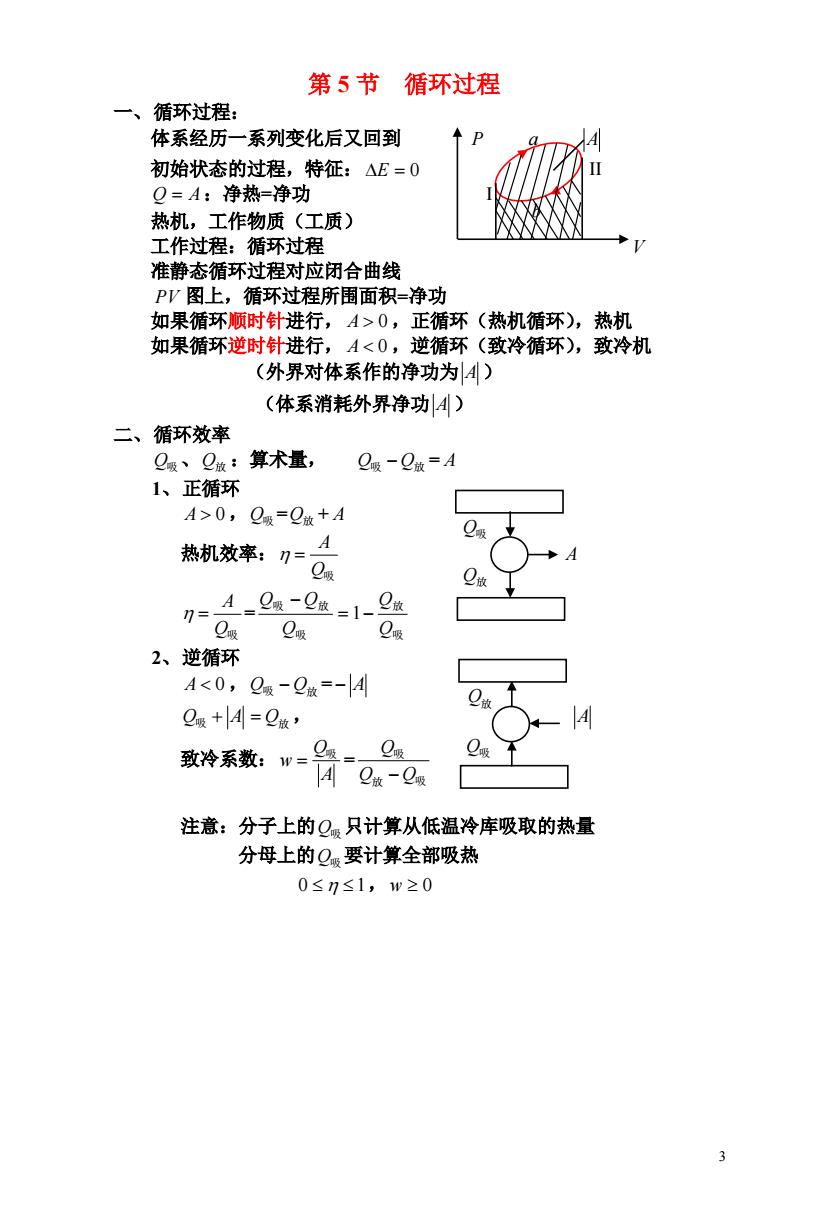
第5节 循环过程 一、 循环过程: 体系经历一系列变化后又回到 初始状态的过程,特征:△E=0 Q=A:净热=净功 热机,工作物质(工质) 工作过程:循环过程 准静态循环过程对应闭合曲线 PV图上,循环过程所围面积=净功 如果循环顺时针进行,A>0,正循环(热机循环),热机 如果循环逆时针进行,A0,Q哪=Q放+A 热机效率:刀=A 吸 7=A-2-0=1- Q吸 Q吸 Q吸 2、逆循环 A<0,Q级-Q做=-4 Q吸+A=Q放, 致冷系数:w= 9级=0吸 注意:分子上的Q吸只计算从低温冷库吸取的热量 分母上的Q要计算全部吸热 0≤7≤1,1w≥0
3 第 5 节 循环过程 一、循环过程: 体系经历一系列变化后又回到 P a A 初始状态的过程,特征:E 0 Q A:净热=净功 热机,工作物质(工质) 工作过程:循环过程 V 准静态循环过程对应闭合曲线 PV 图上,循环过程所围面积=净功 如果循环顺时针进行, A 0 ,正循环(热机循环),热机 如果循环逆时针进行, A 0 ,逆循环(致冷循环),致冷机 (外界对体系作的净功为 A ) (体系消耗外界净功 A ) 二、循环效率 Q吸 、Q放 :算术量, Q吸 Q放 = A 1、正循环 A 0 ,Q吸 =Q放 + A 热机效率: Q吸 A A = Q吸 A 吸 放 吸 吸 放 Q Q Q Q Q 1 2、逆循环 A 0 ,Q吸 Q放 = A Q吸 A Q放 , A 致冷系数: = A Q w 吸 放 吸 吸 Q Q Q 注意:分子上的Q吸 只计算从低温冷库吸取的热量 分母上的Q吸 要计算全部吸热 0 1, w 0 Q放 b Q吸 Q吸 Q放

三、卡诺循环:准静态循环,理想气体,两个等温+两个绝热过程 P T>T a('.,T) 吸 b(Vi:T) d 0放 (Va.T2) c(',I2) Q放 T Qa =vRTiln ,Qa=RT,h VRT,In A-1- 0-1- Q吸吸 vRT In b bc:TVy-=TV- da:Tv=Tvy- -1号 注意:1、两个热源,2、n仅由T和T,决定,3、7T a(Va:T) 9放 b(Vi:T) 4 Q吸 (Va,T2)/ cVe,T2) Q吸 T V Q吸=RTln 2,Q放=RTln vRT,In 吸」 40做-0吸RI V-VRTIn Ws T-T 4
4 三、卡诺循环:准静态循环,理想气体,两个等温+两个绝热过程 P T1 T2 ( , ) a Va T1 Q吸 Q吸 ( , ) b Vb T1 A d Q放 ( , ) Vd T2 ( , ) V T2 c c Q放 T2 V ,a b V V Q吸 RT1 ln d c V V Q放 RT2 ln = = Q吸 A 吸 放 Q Q 1 a b d c V V RT V V RT ln ln 1 1 2 bc : 1 2 1 1 T Vb T Vc da : 1 2 1 1 T Va T Vd ( ) 1 ( ) 1 , d c a b V V V V d c a b V V V V 1 2 1 T T 注意:1、两个热源,2、 仅由T1 和T2 决定,3、 1 让卡诺循环逆向进行 P T1 T2 ( , ) a Va T1 Q放 Q放 ( , ) b Vb T1 A d Q吸 ( , ) Vd T2 ( , ) V T2 c c Q吸 T2 V ,d c V V Q吸 RT2 ln a b V V Q放 RT1 ln = = A Q w 吸 放 吸 吸 Q Q Q d c a b d c V V RT V V RT V V RT ln ln ln 1 2 2 1 2 2 T T T w
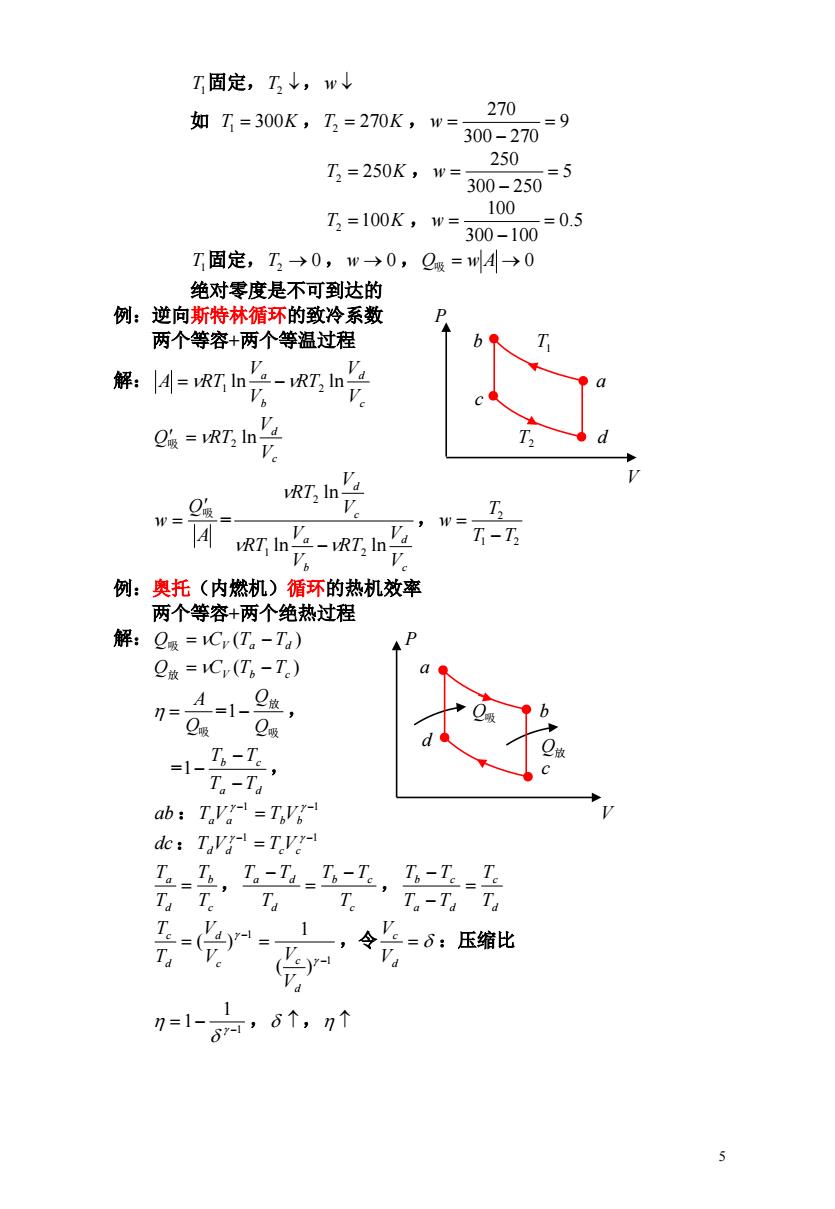
T固定,T,↓,w↓ 270 如T=300K,T,=270K,w= =9 300-270 ☑=250K,w= 250 =5 300-250 100 T,=100K,w= =0.5 300-100 T固定,T2→0,w→0,Q吸=wA→0 绝对零度是不可到达的 例:逆向斯特林循环的致冷系数 P 两个等容+两个等温过程 b 解:A=RTln In 袋=RT,n' 级= In V 1= T vRT In-vRT In T-T V 例:奥托(内燃机)循环的热机效率 两个等容+两个绝热过程 解:Q吸=Cr(T。-Ta) 放=Cr(T6-T) A 7= -=1- Q吸Q吸 =1--, T。-Td ab:Tv=TV de:Tav=Tv- Ta Te Ta T。 Ta-Ta Ta V 是 1 令 e=6:压缩比 7=1、1 ,6个,刀个 5
5 T1 固定,T2 , w 如 T1 300K ,T2 270K , 9 300 270 270 w T2 250K , 5 300 250 250 w T2 100K , 0.5 300 100 100 w T1 固定,T2 0 , w 0 ,Q吸 w A 0 绝对零度是不可到达的 例:逆向斯特林循环的致冷系数 P 两个等容+两个等温过程 b T1 解: cd b a V V RT V V A RT1 ln 2 ln a cd V V Q吸 RT2 ln T2 d = , A Q w 吸 cd b a cd V V RT V V RT V V RT ln ln ln 1 2 2 1 2 2 T T T w 例:奥托(内燃机)循环的热机效率 两个等容+两个绝热过程 解: ( ) Q吸 CV Ta Td P ( ) Q放 CV Tb Tc a = , Q吸 A 吸 放 Q Q 1 Q吸 b = , a d b c T T T T 1 c ab : 1 1 TaVa TbVb V dc: 1 1 TdVd TcVc , , cb d a T T T T c b c d a d T T T T T T d c a d b c T T T T T T ,令 :压缩比 1 1 ( ) 1 ( ) d c c d d c V V V V T T d c V V 1 , , 1 1 Q放 c V d