
第11节自然光与偏振光 一、自然光 (a), b), (c) 自然光在垂直传播方向的平面内: 沿任何一个方向的光振动都不比其它方向占优势 光的能量沿各个方向均匀分布 自然光可以分解为两个相互垂直、彼此独立的等幅分振动 +hr 二、 偏振光 1、完全偏振光(线偏振光,平面偏振光) 传播方向与振动方向决定的平面:振动面 ◆●●+ 2、部分偏振光 H中 十中4 具有偏振现象是横波的特征,纵波没有偏振现象 第12节 偏振片马吕斯定律 一、偏振片:只让某一方向的光振动通过 偏振化方向(起偏方向)个 1、起偏、起偏器 2、检偏、检偏器 HHHO 示教 二、马吕斯定律 线偏振光通过一个偏振片后,透 射光强I与入射光强1。之间满足 1=1。cos2a—马昌斯定律 :入射线偏振光振动方向与偏振片偏振化方向的夹角 证:设入射线偏振光的振幅A, A=Ao cosa,A =A0 sina 1A 1A6 -cos2 a,I=1o cos2 a
1 第 11 节 自然光与偏振光 一、自然光 y c y c y c x x x E z z (a), (b), (c) 自然光在垂直传播方向的平面内: 沿任何一个方向的光振动都不比其它方向占优势 光的能量沿各个方向均匀分布 自然光可以分解为两个相互垂直、彼此独立的等幅分振动 二、偏振光 1、完全偏振光(线偏振光,平面偏振光) 传播方向与振动方向决定的平面:振动面 2、部分偏振光 具有偏振现象是横波的特征,纵波没有偏振现象 第 12 节 偏振片 马吕斯定律 一、偏振片:只让某一方向的光振动通过 偏振化方向(起偏方向) 1、起偏、起偏器 2、检偏、检偏器 A B 示教 二、马吕斯定律 线偏振光通过一个偏振片后,透 射光强 I 与入射光强 I 0 之间满足 马吕斯定律 2 0 I I cos 0 I I :入射线偏振光振动方向与偏振片偏振化方向的夹角 证:设入射线偏振光的振幅 A0 A0 cos , A// A0 A A0 sin A A// , 2 2 0 2 // 0 cos A A I I 2 0 I I cos

注意:只对入射线偏振光成立 若入射光是自然光,1三。 讨论:=0,1=10 OH a=π/2,I=0 HHG一 入射光 旋转偏振片 透射光 线偏振光 明暗交替变化 自然光 光强不变 部分偏振光 强弱交替变化 例:1 让一束自然光通过两个 偏振化方向相互垂直的 偏振片,透射光强=? 如果在两个偏振片之间 加上另一个偏振片,其 偏振化方向与第一个偏 振偏振化方向夹角为α, 透射光强1=,cos2asin2a 如果每个偏振片吸收10%的平行于偏振化方向的光振动能量 透射光强1=,·90%c0s2a-90%sin2a-90% 2 第13节反射和折射光的偏振 入射面:Π(入射线,法线) 反射定律'=i 折射定律n,sini=n2sinY M 反射光和折射光都是部分偏振光 反射光中,“⊥振动”多于“振动” 折射光中,“振动”多于“⊥振动” i=。=arcg2时 反射光为完全偏振光,只包含“1振动” i6:布儒斯特角(起偏角) g。=:布儒斯特定律 n, 注意:(1)i=i。时,只反射部分“1振动”,不反射“1振动” 折射光中包含其余的“⊥振动”和全部的“/振动” 折射光仍是部分偏振光 2
2 注意:只对入射线偏振光成立 若入射光是自然光, 0 2 1 I I 讨论: 0, 0 I I / 2, I 0 入射光 旋转偏振片 透射光 线偏振光 明暗交替变化 自然光 光强不变 部分偏振光 强弱交替变化 例:让一束自然光通过两个 偏振化方向相互垂直的 偏振片,透射光强=? 如果在两个偏振片之间 加上另一个偏振片,其 偏振化方向与第一个偏 振偏振化方向夹角为 , 透射光强 2 2 0 cos sin 2 1 I I 如果每个偏振片吸收10% 的平行于偏振化方向的光振动能量 透射光强 90% cos 90% sin 90% 2 1 2 2 0 I I 第 13 节 反射和折射光的偏振 入射面: (入射线,法线) 反射定律i i i i n1 折射定律 sin sin 1 n2 n i M M 反射光和折射光都是部分偏振光 2 n 反射光中,“ 振动”多于“//振动” 折射光中,“//振动”多于“ 振动” 时 1 2 0 n n i i arctg 0 i 0 i n1 反射光为完全偏振光,只包含“ 振动” :布儒斯特角(起偏角) 0 i 2 n :布儒斯特定律 1 2 0 n n tgi 注意:(1)i i0 时,只反射部分“ 振动”,不反射“//振动” 折射光中包含其余的“ 振动”和全部的“//振动” 折射光仍是部分偏振光 2
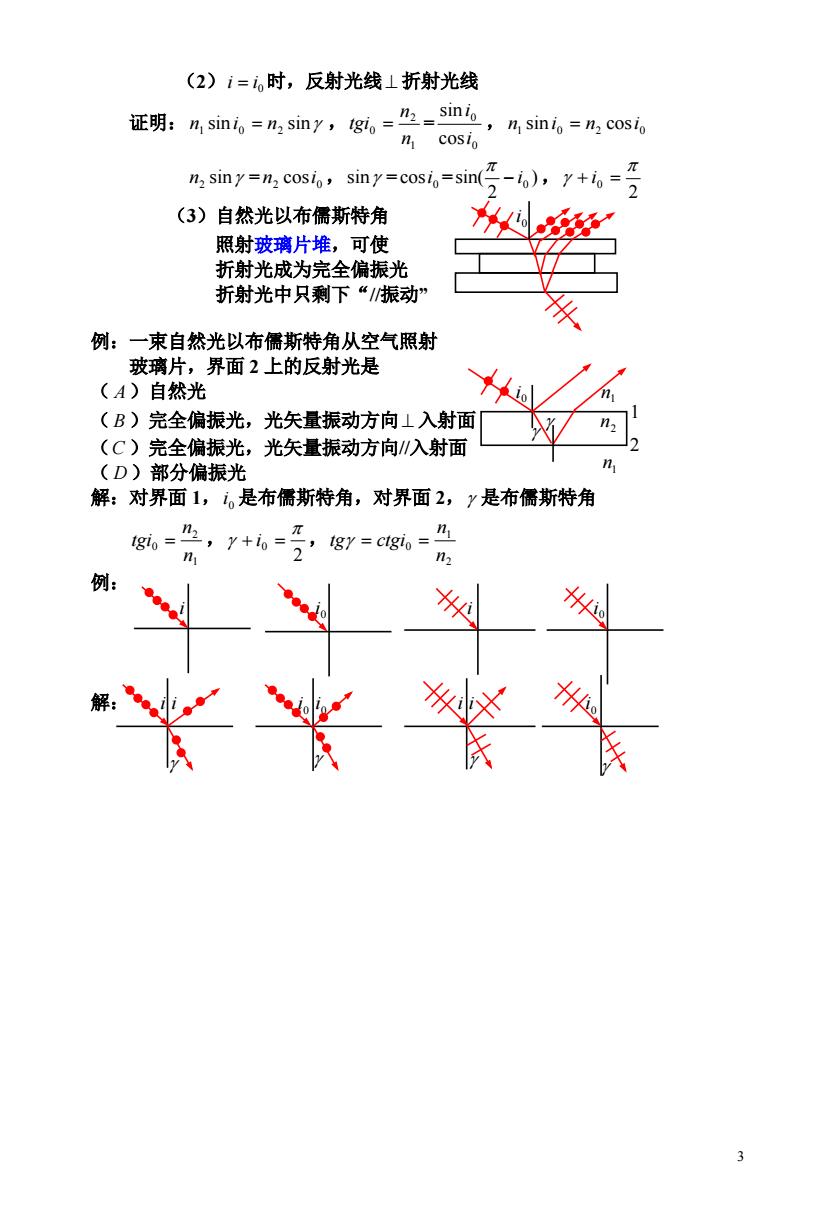
(2)i=,时,反射光线⊥折射光线 证明:%sin=m,siny,g,=2-sna n sinio=n2 cosio n cosio n siny=n2 cosio,siny=cosio=sin(), (3)自然光以布儒斯特角 照射玻璃片堆,可使 折射光成为完全偏振光 折射光中只剩下“振动” 例:一束自然光以布儒斯特角从空气照射 玻璃片,界面2上的反射光是 (A)自然光 io (B)完全偏振光,光矢量振动方向⊥入射面 (C)完全偏振光,光矢量振动方向∥入射面 (D)部分偏振光 解:对界面1,i。是布儒斯特角,对界面2,y是布儒斯特角 g,-,7+6=子gy=g。= n n 例: 3
3 (2)i i0 时,反射光线 折射光线 证明:n1 sin i0 n2 sin , = , 1 2 0 n n tgi 0 0 cos sin i i 1 0 2 0 n sin i n cosi n2 sin = n2 cosi0 ,sin =cosi0 = ) , 2 sin( 0 i 2 0 i (3)自然光以布儒斯特角 0 i 照射玻璃片堆,可使 折射光成为完全偏振光 折射光中只剩下“//振动” 例:一束自然光以布儒斯特角从空气照射 玻璃片,界面 2 上的反射光是 ( A)自然光 0 i n1 ( B )完全偏振光,光矢量振动方向 入射面 2 n (C )完全偏振光,光矢量振动方向//入射面 ( D )部分偏振光 解:对界面 1,i0 是布儒斯特角,对界面 2, 是布儒斯特角 , , 1 2 0 n n tgi 2 0 i 2 1 0 n n tg ctgi 例: i 0 i i 0 i 解: i i 0 i 0 i i i 0 i 1 2 n1