西安电子科技大学：《大学物理》课程教学讲义（下）13-4 光栅衍射

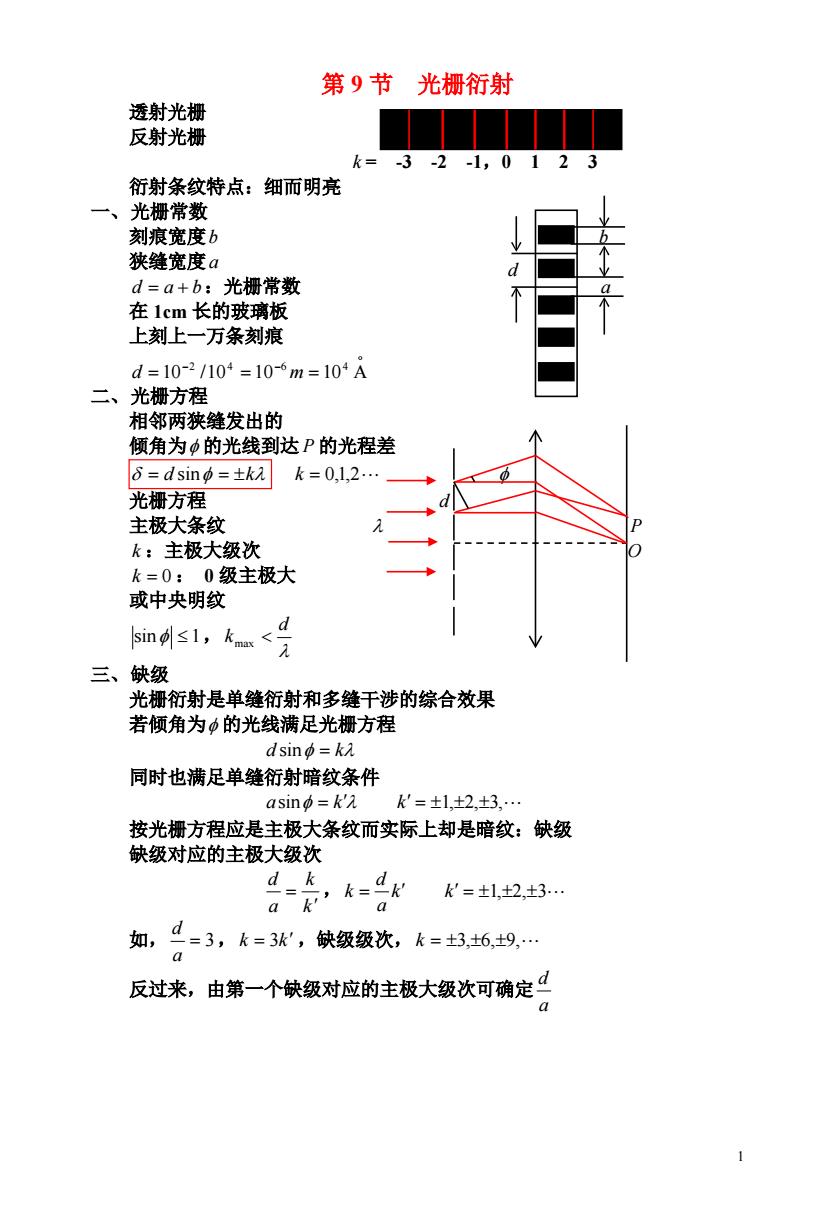
第9节光栅行射 透射光栅 反射光栅 k=-3-2-1,0123 衍射条纹特点：细而明亮 一、光栅常数 刻痕宽度b 狭缝宽度a d d=a+b:光栅常数 在1cm长的玻璃板 上刻上一万条刻痕 d=10-2/104=10-6m=104A 二、光栅方程 相邻两狭缝发出的 倾角为中的光线到达P的光程差 6=dsin中=±k k=012. 光栅方程 主极大条纹 k:主极大级次 k=0:0级主极大 或中央明纹 sinds1,kamd 三、缺级 光栅衍射是单缝衍射和多缝干涉的综合效果 若倾角为中的光线满足光栅方程 dsin中=ka 同时也满足单缝衍射暗纹条件 asino=k'入 k=±1，±2，±3，… 按光栅方程应是主极大条纹而实际上却是暗纹：缺级 缺级对应的主极大级次 日=，k=已 d k k'=±1.+2.±3. a k' 如， d=3,k=3张'，缺级级次，k=±3,6,9，… a 反过来，由第一个峡级对应的主极大级次可确定 1

1 第 9 节 光栅衍射 透射光栅 反射光栅 k = -3 -2 -1，0 1 2 3 衍射条纹特点：细而明亮 一、光栅常数 刻痕宽度b b 狭缝宽度a d  a  b：光栅常数 a 在 1cm 长的玻璃板 上刻上一万条刻痕     A 2 4 6 4 d 10 /10 10 m 10 二、光栅方程 相邻两狭缝发出的 倾角为 的光线到达 P 的光程差   d sin  k k  0,1,2  光栅方程 d 主极大条纹  P k ：主极大级次 O k  0 ： 0 级主极大 或中央明纹 sin  1，  d kmax  三、缺级 光栅衍射是单缝衍射和多缝干涉的综合效果 若倾角为 的光线满足光栅方程 d sin  k 同时也满足单缝衍射暗纹条件 asin  k k  1,2,3, 按光栅方程应是主极大条纹而实际上却是暗纹：缺级 缺级对应的主极大级次 ，k k a d    k k  1,2,3 a d k 如，  3， ，缺级级次， a d k  3k k  3,6,9, 反过来，由第一个缺级对应的主极大级次可确定 a d d

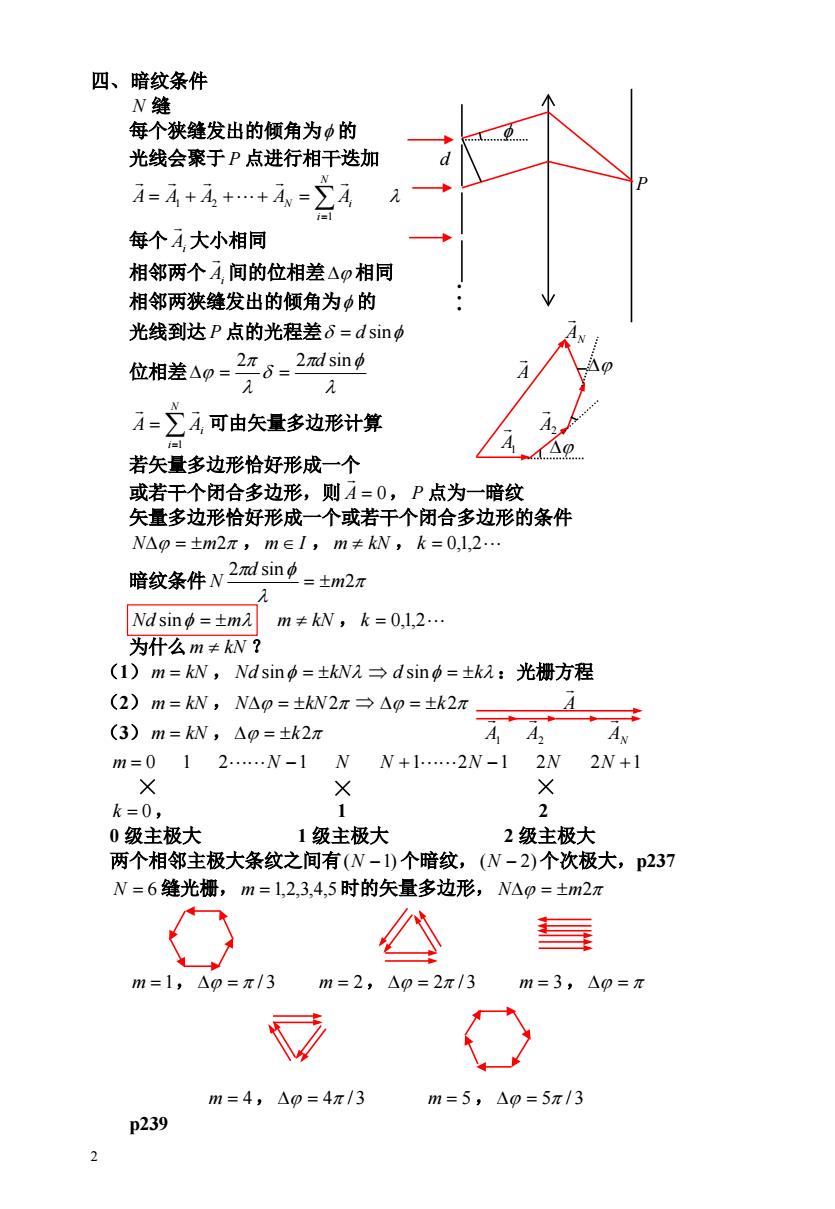
四、暗纹条件 N缝 每个狭缝发出的倾角为中的 光线会聚于P点进行相干迭加 A=+++- 每个A大小相同 相邻两个A,间的位相差△0相同 相邻两狭缝发出的倾角为·的 光线到达P点的光程差6=dsin中 位相差A0=2r6=2sin2 A=之4，可由矢量多边形计算 10 若矢量多边形恰好形成一个 或若干个闭合多边形，则A=0,P点为一暗纹 矢量多边形恰好形成一个或若干个闭合多边形的条件 N△p=±m2π，m∈1，m≠kN,k=0,1,2 暗纹条件v2lsin =土m2π Nd sin中=±mz m≠kN,k=0,1,2 为什么m≠kW? (1)m=kN,Nd sin中=±kN2→dsin中=±k:光栅方程 (2)m=kN,N△p=±kN2π→△p=±k2π A (3)m=kN,△0=±k2元 AA, AN m=012..N-1 N N+1…2N-1 2N 2N+1 × k=0, 1 2 0级主极大 1级主极大 2级主极大 两个相邻主极大条纹之间有(N-1)个暗纹，(N-2)个次极大，p237 N=6缝光栅，m=1,2,3,4,5时的矢量多边形，N△p=±m2π m=1,△0=π/3 m=2,△0=2π/3 m=3,△p=π m=4,△0=4π/3 m=5,△0=5π/3 p239

2 A1 四、暗纹条件 N 缝 每个狭缝发出的倾角为 的  光线会聚于 P 点进行相干迭加 d        N i A A A AN Ai 1 1 2        每个 Ai 大小相同  相邻两个 Ai 间的位相差 相同   相邻两狭缝发出的倾角为 的 光线到达 P 点的光程差  d sin AN 位相差        2 2 d sin    A   可由矢量多边形计算   N i A Ai 1   A2  若矢量多边形恰好形成一个 或若干个闭合多边形，则 A  0， 点为一暗纹  P 矢量多边形恰好形成一个或若干个闭合多边形的条件 N  m2 ，m  I ，m  kN ，k  0,1,2 暗纹条件     2 2 sin m d N   Nd sin  m m  kN ，k  0,1,2 为什么m  kN ？ （1）m  kN ， Nd sin  kN  d sin  k ：光栅方程 （2）m  kN ， N  kN2    k2 A  （3）m  kN ，  k2 A1  A2  AN m  0 1 2N 1 N N 12N 1 2N 2N 1 k  0， 1 2 0 级主极大 1 级主极大 2 级主极大 两个相邻主极大条纹之间有(N 1) 个暗纹，(N  2)个次极大，p237 N  6 缝光栅，m  1,2,3,4,5 时的矢量多边形， N  m2 m  1，   / 3 m  2，  2 / 3 m  3，   m  4，  4 / 3 m  5，  5 / 3 p239    P

只能观察到主极大条纹 N=2:双缝同样成立 N个，主极大条纹越细越明亮，p236 五、衍射光谱 dsin中=±ka 主极大条纹的坐标x=fg中≈f.sin=±kf2/d,k=0,l,2 相邻两个主极大条纹间距△x=f/d d一定，2个，△x↑ 用日光做实验，除中央亮纹为白色条纹外，两侧为彩色光谱 0, 2 d 白紫 红紫 紫红 红 干涉与衍射都是波的相干迭加 干涉一般是指两束或几束光的相干迭加 衍射则是无穷多个子波的相干迭加 计算合振动时，干涉用求和的方法，衍射用积分的方法 例：用=5000A的单色光照射d=2.10m,a=0.700m的光栅 求：（1)垂直照射(2)斜入射i=30.0°，能看到哪几级光谱线？ 解：(1)dsin=±k2,k=dsin2<d-2.10x106 2。,月5000×10-m=42,9=3 k=±3为缺级，-4,2,1,0,1,2,4共7条光谱线 (2)6=dsin-dsini=d(sino-sini) d(sinp-sini)=±k2,k=0,l,2… 中=90 k=dsin90-sin30）=2.1 中=-90° k=dsin-90)-sin309]=-6.3 入 d=3,k=-6,-3为缺级 实际能看到-5，-4，-2，-1,0,1,2共7条光谱线 注：平行光斜入射时，单缝衍射暗纹条件为 a(sinp-sini)=±k'2,k'=1,2,3,… 光栅方程d(sin中-sini)=士k,k=0,l,2,… 缺级仍由k=已k k=±1，+2，±3…决定 3

3 只能观察到主极大条纹 N  2：双缝同样成立 N ，主极大条纹越细越明亮，p236 五、衍射光谱 d sin  k 主极大条纹的坐标 x  f tg  f sin  kf / d ，k  0,1,2 相邻两个主极大条纹间距x  f / d d 一定，  ，x  用日光做实验，除中央亮纹为白色条纹外，两侧为彩色光谱 0， 1 2 3 白 紫 红 紫 紫 红 红 干涉与衍射都是波的相干迭加 干涉一般是指两束或几束光的相干迭加 衍射则是无穷多个子波的相干迭加 计算合振动时，干涉用求和的方法，衍射用积分的方法 例：用 的单色光照射 ， 的光栅    5000A d  2.10m a  0.700m 求：（1）垂直照射（2）斜入射i  30.0  ，能看到哪几级光谱线？ 解：（1）d sin  k ， 4.2 ， 5000 10 sin 2.10 10 10 6           d  d k  3 a d k  3为缺级，-4，-2，-1，0，1，2，4 共 7 条光谱线 （2）  d sin  d sin i  d(sin  sin i) d(sin  sin i)  k ，k  0,1,2  P    90 d 2.1 (sin90 sin30 )       d k    90 6.3 [sin( 90 ) sin30 ]         d k  3， 为缺级 a d k  6,3 实际能看到-5，-4，-2，-1，0，1，2 共 7 条光谱线 注：平行光斜入射时，单缝衍射暗纹条件为 a(sin  sin i)  k ，k  1,2,3, 光栅方程 d(sin  sin i)  k ，k  0,1,2, 缺级仍由  k k  1,2,3决定 a d k i 

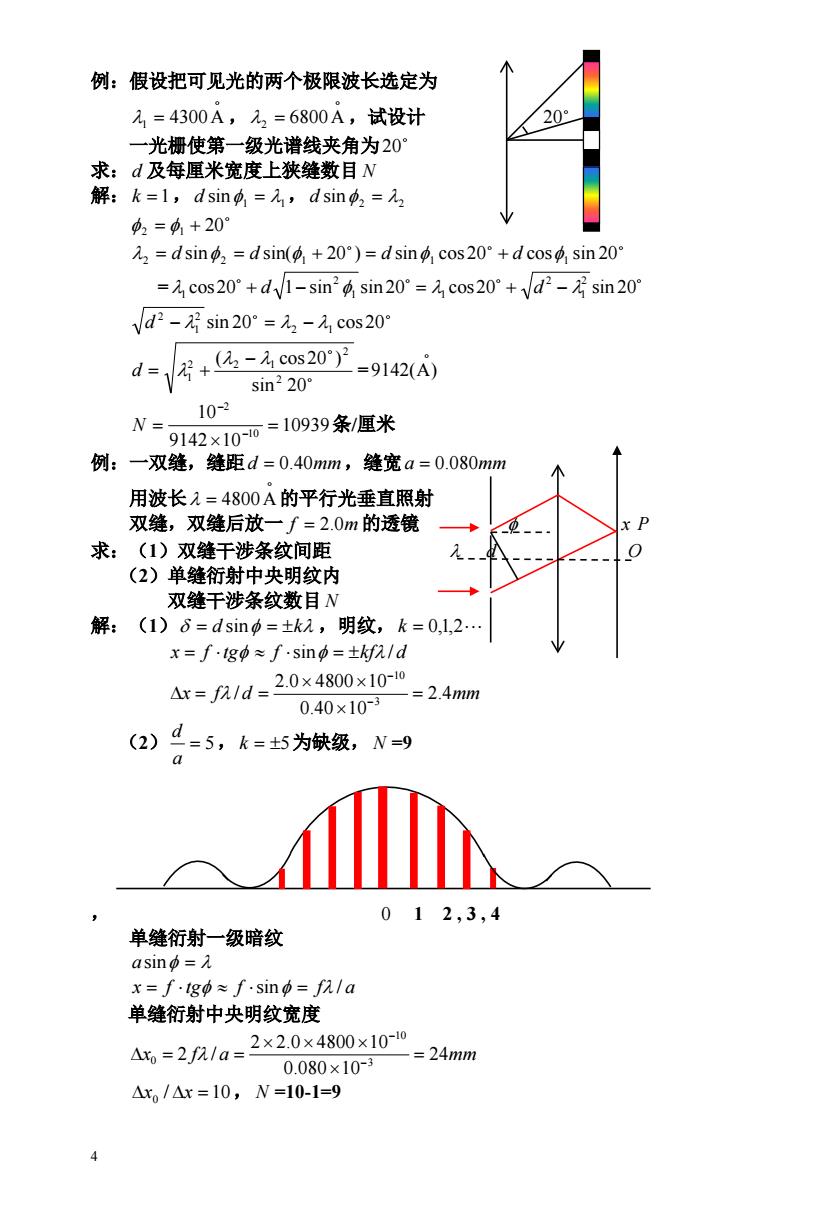
例：假设把可见光的两个极限波长选定为 1=4300A,22=6800A,试设计 209 一光栅使第一级光谱线夹角为20 求：d及每厘米宽度上狭缝数目N 解：k=1,dsin中，=乙，d sino2= p2=41+20 元2=dsin2=dsin(p,+20)=d sin cos20°+d cos sin20° =cos20°+dV1-sin24sin20°=2，cos20°+Vd2-乃sin20° Vd2-sin20°=元2-1cos20° d=居+620T=9142X0 sin220 10-2 N= 9142x10-10=10939条/厘米 例：一双缝，缝距d=0.40mm,缝宽a=0.080mm 用波长1=4800A的平行光垂直照射 双缝，双缝后放一∫=2.0m的透镜 求：（1)双缝干涉条纹间距 (2)单缝衍射中央明纹内 双缝干涉条纹数目N 解：(1)6=dsin=±k,明纹，k=0,l2 x=f.tg中≈f.sinφ=±kfn/d Ar=a/d=2.0x4800x10- -=2.4mwm 0.40×10-3 (2) d=5,k=±5为缺级，N=9 012,3,4 单缝衍射一级暗纹 asino=元 x=f·tgφ≈f·sinp=fIa 单缝衍射中央明纹宽度 A,=2fn1a=2×2.0x4800×10-0 =24mm 0.080×10-3 △xo/△x=10,N=10-1=9 4

4 例：假设把可见光的两个极限波长选定为 ， ，试设计  1  4300A  2  6800A  20 一光栅使第一级光谱线夹角为  20 求：d 及每厘米宽度上狭缝数目 N 解：k  1，d sin1  1 ， 2 2 d sin     2  1  20    2  d sin 2  d sin(1  20 )  d sin1 cos 20  d cos1 sin 20 =     cos20 1 sin sin 20 cos20 sin 20 2 1 2 1 1 2 1  d      d     sin 20 2 1 cos 20 2 1 2 d       =   sin 20 ( cos 20 ) 2 2 2 2 1 1     d    9142(A) 10939条/厘米 9142 10 10 10 2      N 例：一双缝，缝距d  0.40mm，缝宽a  0.080mm 用波长 的平行光垂直照射    4800A 双缝，双缝后放一 f  2.0m 的透镜  x P 求：（1）双缝干涉条纹间距  d O （2）单缝衍射中央明纹内 双缝干涉条纹数目 N 解：（1）  d sin  k ，明纹，k  0,1,2 x  f tg  f sin  kf / d x f d 2.4mm 0.40 10 2.0 4800 10 / 3 10           （2）  5， 为缺级， =9 a d k  5 N ， 0 1 2 , 3 , 4 单缝衍射一级暗纹 asin   x  f tg  f sin  f / a 单缝衍射中央明纹宽度 x f a 24mm 0.080 10 2 2.0 4800 10 2 / 3 10 0            x0 / x  10， N =10-1=9

第10节X射线布拉格方程 1895年，X射线（伦琴射线），波长：0.1A~100A 1912年，劳厄，天然晶体，透射光栅，观察到X射线衍射现象 证明了X射线是电磁波 布拉格父子，把晶体作为反射光栅 d:晶格常数（晶面间距），中：掠射角 上下两个晶面产生的两束反射X射线的光程差 δ=AC+CB=2dsin中 2dsin中=k1,k=1,2,3,…,强反射 布拉格方程 应用：(1)已知d求入(2)已知1求d,晶体结构分析

5 第 10 节 射线 布拉格方程 1895 年，  射线（伦琴射线），波长：   0.1A ~ 100A 1912 年，劳厄，天然晶体，透射光栅，观察到  射线衍射现象 证明了  射线是电磁波 布拉格父子，把晶体作为反射光栅  D A B C d ：晶格常数（晶面间距）， ：掠射角 上下两个晶面产生的两束反射  射线的光程差   AC  CB = 2d sin 2d sin  k ，k  1,2,3,，强反射 布拉格方程 应用：（1）已知d 求 （2）已知 求d ，晶体结构分析  d d