西安电子科技大学：《大学物理》课程教学讲义（下）11-1 稳恒电流的磁场

稳恒电流的磁场 第1节1 磁场与磁感应强度 一、磁场 运动电荷 运动电荷 载流导线 台磁场台 载流导线 磁 体 磁 体 稳恒电流：不随时间变化的电流 二、磁感应强度B B B的方向：静止磁针的N极指向 电流元（矢量)：dl 大小：Idl 方向：沿电流方向 dF o Idlsin 同一位置： 、 dF 恒定 Idlsin 与电流元无关 dF 不同位置： 一 般不同，与磁场中位置有关 Idlsin0 dF B= dF BIdlsin0 Idlsine' 0=90,IdiB,dF Bldl,B=dFs Idl “磁场中某点处，磁感应强度B是一个矢量，其方向沿 该点处静止磁针的N极指向，其大小等于单位电流元 受到的最大磁场力” SI:N/Am)=T(特斯拉) 第2节 毕奥萨伐尔定律 一、毕奥萨伐尔定律 dB oc Idl sinθ dB=Ho ldlsine dB 2 4元 4:真空磁导率 Idl 0 S:4=4π×10-7N/A2 dBLII(Idl,) 指向：右手螺旋法则 dB=Ho Idlx 4π r3 dB=Ho Idlrsin uo Idlsin 4π r3 4πr2 方向：沿Idl×下 1

1 稳恒电流的磁场 第 1 节 磁场与磁感应强度 一、磁场             磁 体 载流导线 运动电荷 磁场 磁 体 载流导线 运动电荷 稳恒电流：不随时间变化的电流 二、磁感应强度 B  B  B 的方向：静止磁针的 N 极指向 N， N  B  电流元（矢量）： Idl 大小： Idl 方向：沿电流方向 dF  Idlsin 同一位置： 恒定 Idlsin dF 与电流元无关 I 不同位置： 一般不同，与磁场中位置有关 Idlsin dF ， Idlsin dF B  dF  BIdlsin   90  ， Idl B ， ，    dF BIdl m  Idl dF B m  “磁场中某点处，磁感应强度 B 是一个矢量，其方向沿  该点处静止磁针的 N 极指向，其大小等于单位电流元 受到的最大磁场力” SI：N/(Am)=T(特斯拉) 第 2 节 毕奥-萨伐尔定律 一、毕奥-萨伐尔定律 ， 2 sin r Idl dB   2 0 sin 4 r Idl dB     dB   0 ：真空磁导率 Idl P  SI：  0 = 7 4 10    2 N / A dB (Idl ,r)     I L 指向：右手螺旋法则 3 0 4 r Idl r dB        2 0 3 0 sin 4 sin 4 r Idl r Idlr dB         方向：沿 Idl r   r Idl  B   

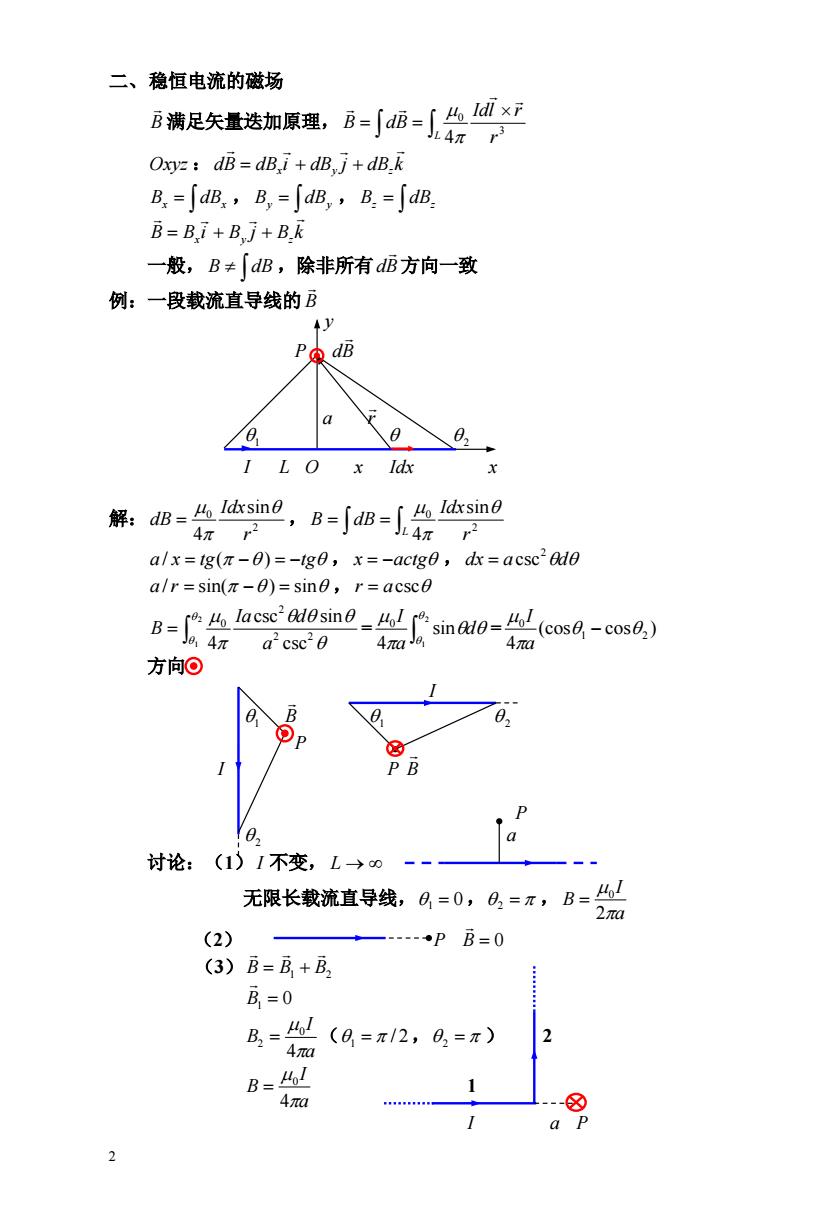
二、稳恒电流的磁场 满足矢蛋选加聚理-6-会 Oxyz:dB=dBi+dB j+dB.k B=∫dB，B,=∫dB,B=∫dB B=Bi+B,j+B.k 一般，B≠「dB，除非所有dB方向一致 例：一段载流直导线的B PodB a 2 I LO x Idx 会2,8==会m9 解：dB=l体sine 2 a/x=g(π-0)=-g0,x=-acg0，dk=acsc2u0 a/r=sin(π-)=sin0,r=acscθ Bacssnsin(coss) J4π a'csc20 4πd 方向⊙ 02 Op PB P 讨论：（1)I不变，L→0 无限长载流直导线，日=0,6，=π，B= 2πa (2) ---•PB=0 (3)B=B+B, B,=0 B.=Mol (0=π/2,02=π) 2 4π B=Hol 1 4πa Q P 2

2 二、稳恒电流的磁场 B 满足矢量迭加原理，       L r Idl r B dB 3 0 4       Oxyz ：dB dB i dB j dB k x y z        Bx   dBx ， By   dBy ，  Bz  dBz B B i B j B k x y z        一般， B   dB ，除非所有dB方向一致  例：一段载流直导线的 B  y P dB  a r 解： 0 2 ， sin 4 r Idx dB         L r Idx B dB 2 0 sin 4    a / x  tg(  )  tg ， x  actg ，dx a d 2  csc a /r  sin(  )  sin ，r  acsc = =   2 1 2 2 2 0 csc csc sin 4         a Ia d B  2 1 sin 4 0       d a I (cos cos ) 4 1 2 0      a I 方向 I 1 B  1  2 P I P B  P  2 a 讨论：（1） I 不变， L   无限长载流直导线，1  0， 2   ， a I B   2 0  （2） P B  0  （3） B B1 B2      B1  0  （ ， ） 2 a I B   4 0 2  1   / 2  2   1 a I B   4 0  I a P 1   2 I L O x Idx x

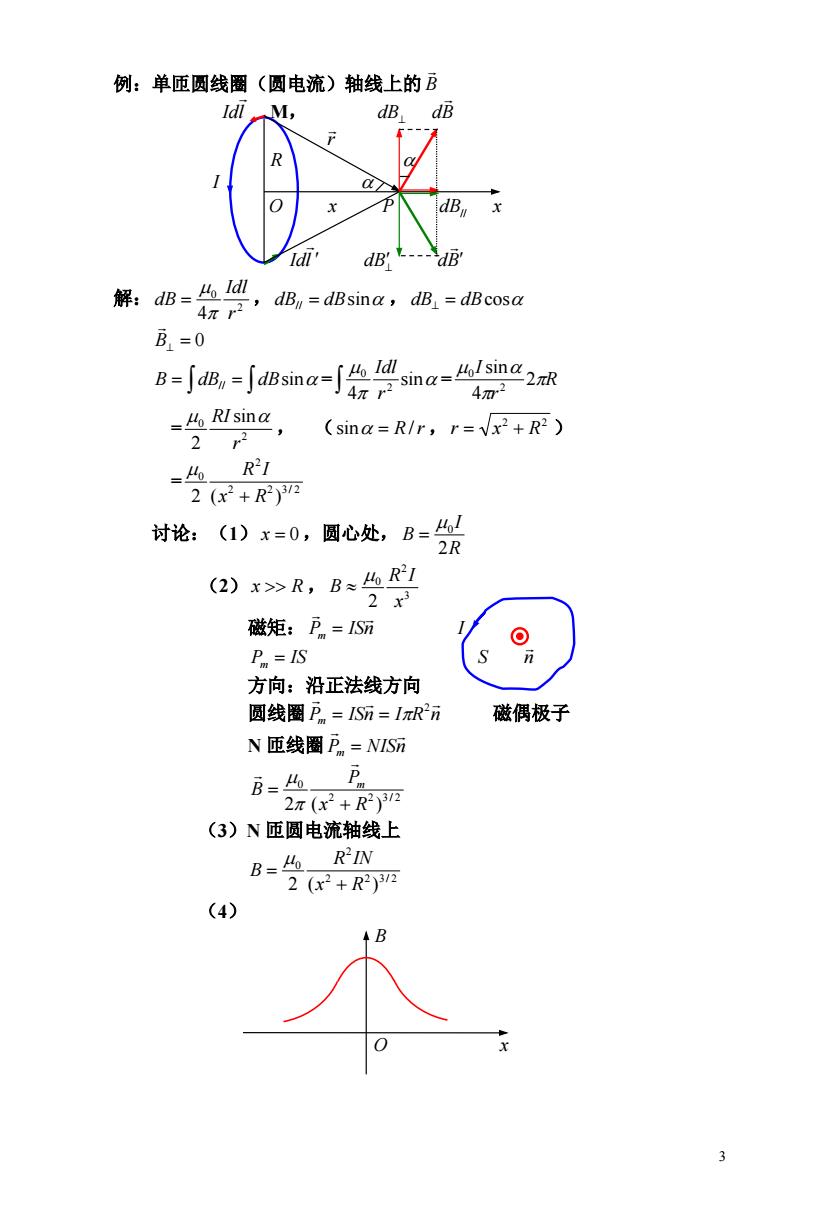
例：单匝圆线圈（圆电流）轴线上的B Idl M, dBdB R dB Idl' dB' dB' 解：dB=,dBu=dBsina,aB=dBcosa B=0 8-∫，-∫Bsna-j绘gna-么42a 4m2 =Ho RI sina 2 2 (sina=R/r,r=Vx2+R2) =46 R21 2(x2+R2)32 讨论：(1)x=0,圆心处，B= 2R (2)x>R,B≈R1 2x3 磁矩：Pn=1S7 Pr IS 方向：沿正法线方向 圆线圈Pn=1Sm=IπRn 磁偶极子 N匝线圈P=NIS防 B= 2π(2+R2)32 (3)N匝圆电流轴线上 B=Ho RIN 2(x2+R2)312 (4)

3 例：单匝圆线圈（圆电流）轴线上的 B  Idl M，  dB dB  r R  I  O x P dB// x Idl    dB dB  解： 0 2 ， ， 4 r Idl dB    dB//  dBsin dB  dBcos B  0  = =   B  dB//  dBsin     sin 4 2 0 r Idl R r I     2 4 sin 2 0 = 0 2 ， （ ， ） sin 2 r  RI  sin  R/r 2 2 r  x  R = 2 2 3 / 2 2 0 2 (x R ) R I   讨论：（1） x  0，圆心处， R I B 2 0  （2） x  R ， 3 2 0 2 x R I B   磁矩： P ISn m    I P IS m  S n  方向：沿正法线方向 圆线圈 Pm ISn I R n 磁偶极子    2    N 匝线圈 Pm NISn    2 2 3 / 2 0 2 (x R ) P B m       （3）N 匝圆电流轴线上 2 2 3 / 2 2 0 2 (x R ) R IN B    （4） B O x

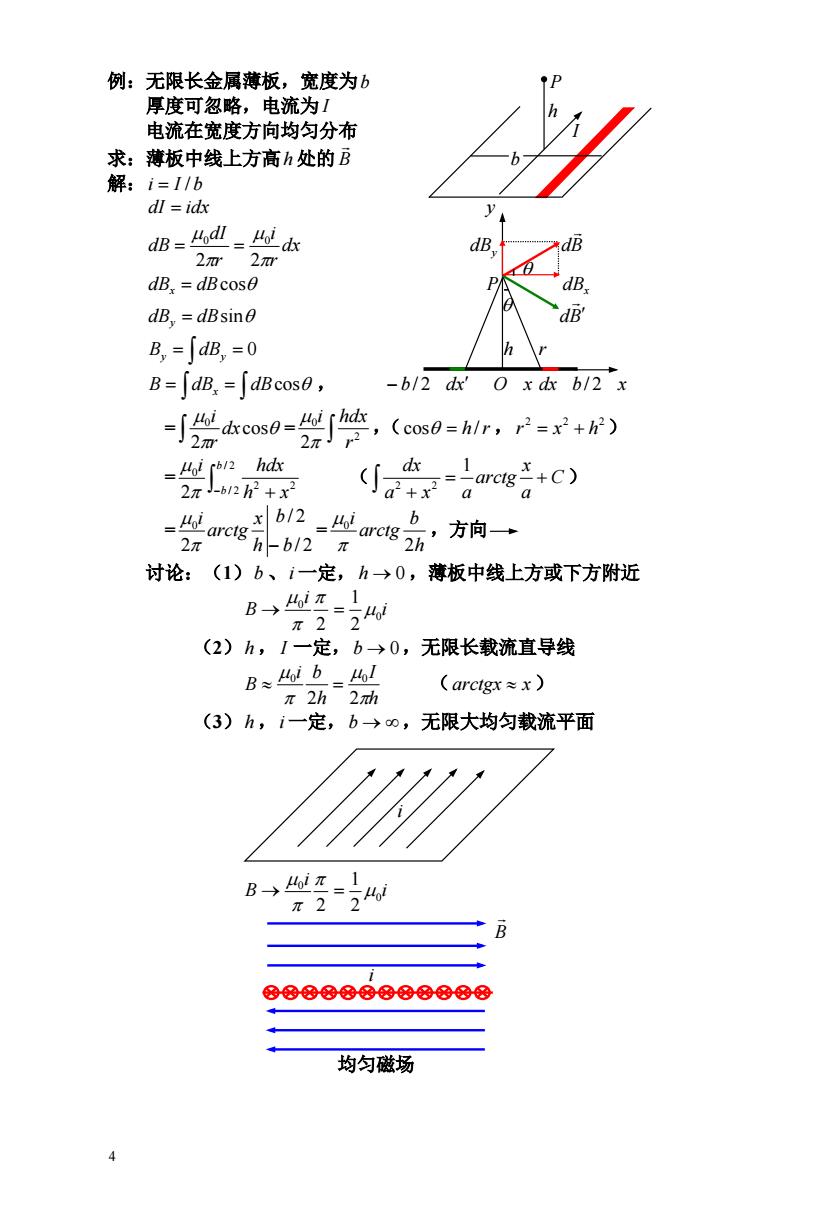
例：无限长金属薄板，宽度为b 厚度可忽略，电流为1 电流在宽度方向均匀分布 求：薄板中线上方高h处的B b 解：i=1/b dl idx dB=4=此本 B 2π2 dB,dBcose dB. dB,=dBsine dB B,=∫dB,=0 h B=∫dB=dBcos8, -b/2 dx'O x dx b/2 x -gm0-兴停，（o0-r,2) =Loi [or2 hdx 2元J-b12h2+x2 ∫4 -+C) a+x x b/2 =arci 2π amg，方向一 h-b/2π 讨论： (1)b、i一定，h→0，薄板中线上方或下方附近 B→π、1 x2=24w (2)h,1一定，b→0，无限长载流直导线 B≈Mb=4l π2h2h （arctgx≈x） (3)h,i一定，b→o,无限大均匀载流平面 B→π、1 元2i4 B 888888888888 均匀磁场 4

4 例：无限长金属薄板，宽度为b P 厚度可忽略，电流为 I 电流在宽度方向均匀分布 I 求：薄板中线上方高h 处的 B  b 解：i  I /b dI  idx y dx r i r dI dB     2 2 0 0   dBy dB  dB dBcos x  P dBx dB dBsin y  dB    0 By  dBy h r ，   B  dBx  dBcos  b / 2 dx O x dx b / 2 x =  = ，（ ， ）   cos 2 0  dx r i  2 0 2 r i hdx   cos  h /r 2 2 2 r  x  h =  （ ）   / 2 / 2 2 2 0 2 b b h x i hdx   C a x arctg a x a dx     1 2 2 = = ，方向 / 2 / 2 2 0 b b h x arctg i    h b arctg i 2 0   讨论：（1）b 、i 一定，h  0 ，薄板中线上方或下方附近 2 0    i B  i0 2 1   （2）h ， I 一定，b  0，无限长载流直导线 （ ） h I h i b B     2 2 0 0   arctgx  x （3）h ，i 一定，b  ，无限大均匀载流平面 i 2 0    i B  i0 2 1   B  i 均匀磁场  h 

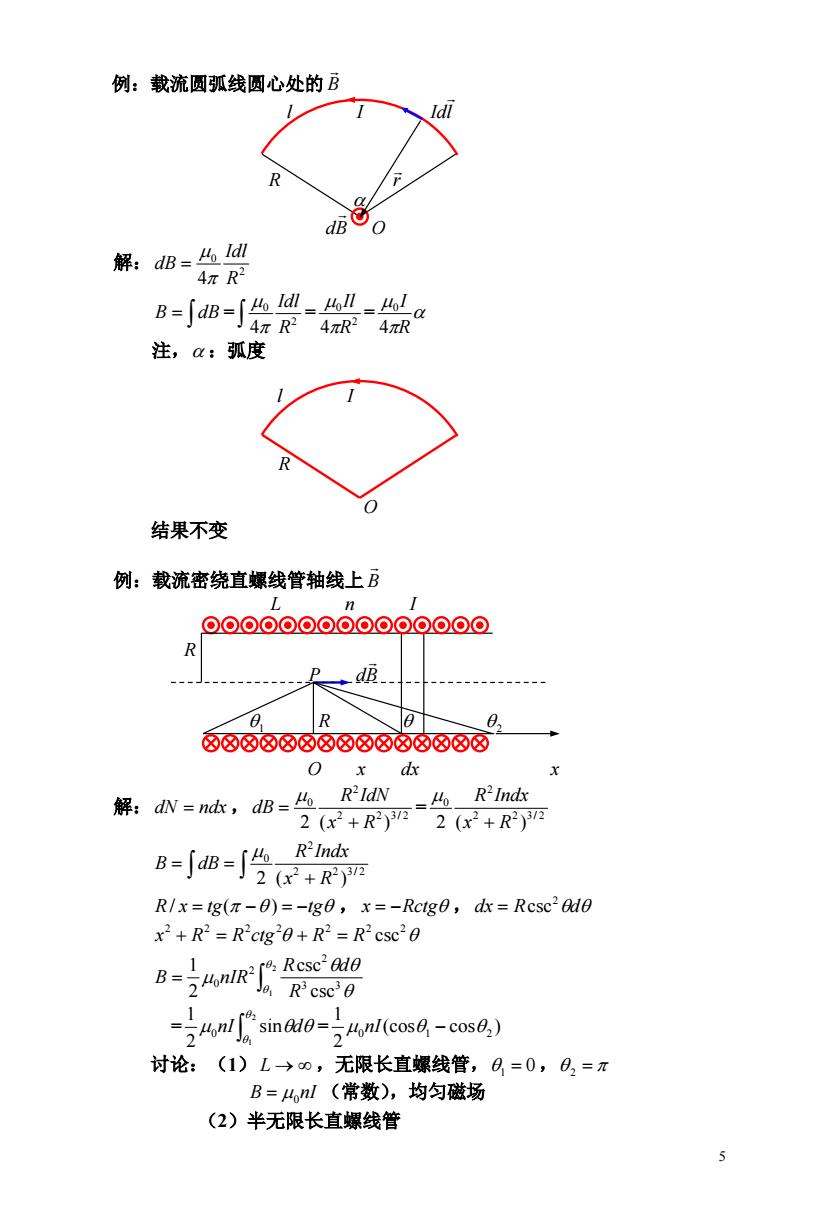
例：载流圆弧线圆心处的B 解：dB=l 4πR B=-会 4πR2 4πR 注，a:弧度 结果不变 例：载流密绕直螺线管轴线上B 00000000000⊙OOO R d e R ⑧⑧⑧88888888⑧⑧88 O x dx X 解：dN=ndk,dB=RIN =Lo R2Indx 2(x2+R2)D2(x2+R2)丽 B==怡r R2Indx R/x=1g(-0)=-1g0,x=-Rctg0,dx=Rcsc20d0 x2+R2=R'ctg20+R2=R2csC20 B=号4onR2a:Rcscddo R3csc30 sinto n(co0cos0) 1 讨论：(1)L→o, 无限长直螺线管，日=0，日2=π B=4,nl(常数)，均匀磁场 (2)半无限长直螺线管 5

5 例：载流圆弧线圆心处的 B  l I Idl R r  dB  O 解： 2 0 4 R Idl dB    = = =  B  dB  2 0 4 R Idl   2 0 4 R Il      R I 4 0 注， ：弧度 l I R O 结果不变 例：载流密绕直螺线管轴线上 B  L n I R P dB  1 R   2 O x dx x 解：dN  ndx ， = 2 2 3 / 2 2 0 2 (x R ) R IdN dB    2 2 3 / 2 2 0 2 (x R ) R Indx        2 2 3 / 2 2 0 2 (x R ) R Indx B dB  R/ x  tg(  )  tg ， x  Rctg ，dx R d 2  csc   2 2 2 2 2 2 2 x  R  R ctg  R  R csc   2 1 3 3 2 2 0 csc csc 2 1       R R d B nIR = =  2 1 sin 2 1 0    nI d (cos cos ) 2 1 0n 1   2 I 讨论：（1） L   ，无限长直螺线管，1  0， 2   B  0nI （常数），均匀磁场 （2）半无限长直螺线管