
一、选择题(每小题3分,共30分) 1.一辆汽车从静止出发在平直公路上加速前进.如果发动机的功率一定,下面哪一种 说法是正确的? ] (A) 汽车的加速度是不变的 (B) 汽车的加速度随时间减小 (C) 汽车的加速度与它的速度成正比 (D) 汽车的速度与它通过的路程成正比 2.卫星绕地球沿椭圆轨道运动,地球在椭圆的一个焦点上,卫星的[ ] (A)动量不守恒,动能守恒 (B) 动量守恒,动能不守恒 (C) 对地心的角动量守恒,动能不守恒 (D) 对地心的角动量不守恒,动能守恒 3.某质点作直线运动的运动学方程为x=35+6,则该质点作[ ] (A)匀加速直线运动,加速度沿x轴正方向 (B)匀加速直线运动,加速度沿x轴负方向 (C)变加速直线运动,加速度沿x轴正方向 (D)变加速直线运动,加速度沿x轴负方向 4.一平面简谐波沿x轴负方向传播。已知x=b处质点的振动方程为 y=ACos(O+o),波速为W,则坐标为x点处振动方程(即波函数)为 C b+x y=Acos[ot+ +p] y=Acosou+ (A) (B) u y=Acos(lt+x-b +o} y=Acosoft+ b-x]+0o3 (C) (D) u 5.把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度日,然 后由静止放手任其振动,从放手时开始计时。若用余弦函数表示其运动方程,则该单摆 振动的初相为 ] (A)元 (B) 元2 (C) 0 (①)8
一、选择题(每小题 3 分,共 30 分) 1. 一辆汽车从静止出发在平直公路上加速前进.如果发动机的功率一定,下面哪一种 说法是正确的? [ ] (A) 汽车的加速度是不变的 (B) 汽车的加速度随时间减小 (C) 汽车的加速度与它的速度成正比 (D) 汽车的速度与它通过的路程成正比 2. 卫星绕地球沿椭圆轨道运动,地球在椭圆的一个焦点上,卫星的[ ] (A) 动量不守恒,动能守恒 (B) 动量守恒,动能不守恒 (C) 对地心的角动量守恒,动能不守恒 (D) 对地心的角动量不守恒,动能守恒 3. 某质点作直线运动的运动学方程为 x=3t-5t 3 + 6,则该质点作 [ ] (A) 匀加速直线运动,加速度沿 x 轴正方向 (B) 匀加速直线运动,加速度沿 x 轴负方向 (C) 变加速直线运动,加速度沿 x 轴正方向 (D) 变加速直线运动,加速度沿 x 轴负方向 4. 一平面简谐波沿 x 轴负方向传播。已知 x = b 处质点的振动方程为 cos( ) 0 y A t ,波速为 u,则坐标为 x 点处振动方程(即波函数)为 [ ] (A) cos[ ] 0 u b x y A t (B) cos{ [ ] } 0 u b x y A t (C) cos{ [ ] } 0 u x b y A t (D) cos{ [ ] } 0 u b x y A t 5. 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度 ,然 后由静止放手任其振动,从放手时开始计时。若用余弦函数表示其运动方程,则该单摆 振动的初相为 [ ] (A) (B) /2 (C) 0 (D)

6.如图所示,A、B为两个相同的绕着轻绳的定滑轮.A滑轮 挂一质量为M的物体,B滑轮受拉力F,而且F=Mg.设A、 B两滑轮的角加速度分别为B和B,不计滑轮轴的摩擦,则 (A)B4=BB (B)B>BB (C)BA<BB (D)不能确定 7.一圆盘正绕垂直于盘面的水平光滑固定轴0转动,如图射 来两个质量相同,速度大小相同,方向相反并在一条直线上 的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间, 圆盘的角速度ω 7 (A)增大 (B)不变 (C)减小 (D)不能确定 8.有一半径为R的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为 J,开始时转台以匀角速度o转动,此时有一质量为m的人站在转台中心.随后人沿 半径向外跑去,当人到达转台边缘时,转台的角速度为 (A) (B) (J+m)R2 @0 (C)0o (D) J+mR2 @o v(m/s) 9.一质点沿x轴作直线运动,其曲线如图所示,如 仁0时,质点位于坐标原点,则5s时,质点在x轴上 2 的位置为 (s) (A)25m (B)2.75m. 0 2 33.545 (C)0 (D)-2m 10.空中有一气球,下连一绳梯,它们的质量共为M.在梯上站一质 量为m的人,起始时气球与人均相对于地面静止.当人相对于绳梯以 速度v向上爬时,气球的速度为(以向上为正)[ ] (A)-mv (B)-Mv (C、mw (D)-(m+M)v m+M m+M M m
6. 如图所示,A、B 为两个相同的绕着轻绳的定滑轮.A 滑轮 挂一质量为 M 的物体,B 滑轮受拉力 F,而且 F=Mg.设 A、 B 两滑轮的角加速度分别为A和B,不计滑轮轴的摩擦,则 [ ] (A) A=B (B) A>B (C) A<B (D) 不能确定 7. 一圆盘正绕垂直于盘面的水平光滑固定轴 O 转动,如图射 来两个质量相同,速度大小相同,方向相反并在一条直线上 的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间, 圆盘的角速度 [ ] (A) 增大 (B) 不变 (C) 减小 (D) 不能确定 8. 有一半径为 R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为 J,开始时转台以匀角速度ω0 转动,此时有一质量为 m 的人站在转台中心.随后人沿 半径向外跑去,当人到达转台边缘时,转台的角速度为 [ ] (A) 2 0 mR J (B) 2 0 J m R J (C) 0 (D) 2 0 J mR J 9. 一质点沿 x 轴作直线运动,其 vt 曲线如图所示,如 t=0 时,质点位于坐标原点,则 t=5 s 时,质点在 x 轴上 的位置为 [ ] (A) 25m (B) 2.75m. (C) 0 (D) 2 m 10. 空中有一气球,下连一绳梯,它们的质量共为 M.在梯上站一质 量为 m 的人,起始时气球与人均相对于地面静止.当人相对于绳梯以 速度 v 向上爬时,气球的速度为(以向上为正)[ ] (A) m M m v (B) m M M v (C) M mv (D) m (m M )v A M B F
二、填空题(每小题3分,共30分) 1.在v-t图中所示的三条直线都表示同一类型的运动, U I、Ⅱ、Ⅲ三条直线表示的是 运动,直 线所表示的运动的加速度最大 2.图中所示的装置中,略去所有摩擦以及滑轮和绳的质 量,且绳不可伸长,则质量为m的物体的加速度1 m 3.一质量为M的弹簧振子,水平放置且静止在平衡位置, 如图所示.一质量为m的子弹以水平速度⑦射入振子中,并 随之一起运动.如果水平面光滑,此后弹簧的最大势能为 4.质量m的小球,以水平速度优与光滑桌面上质量为M的 静止斜劈作完全弹性碰撞(无能量损失)后竖直弹起,则碰 后斜劈的运动速度v= 0-≥ m (m) 5.一简谐振子的振动曲线如图所示,则以余弦函数表示的 0.044 振动方程为 0.04
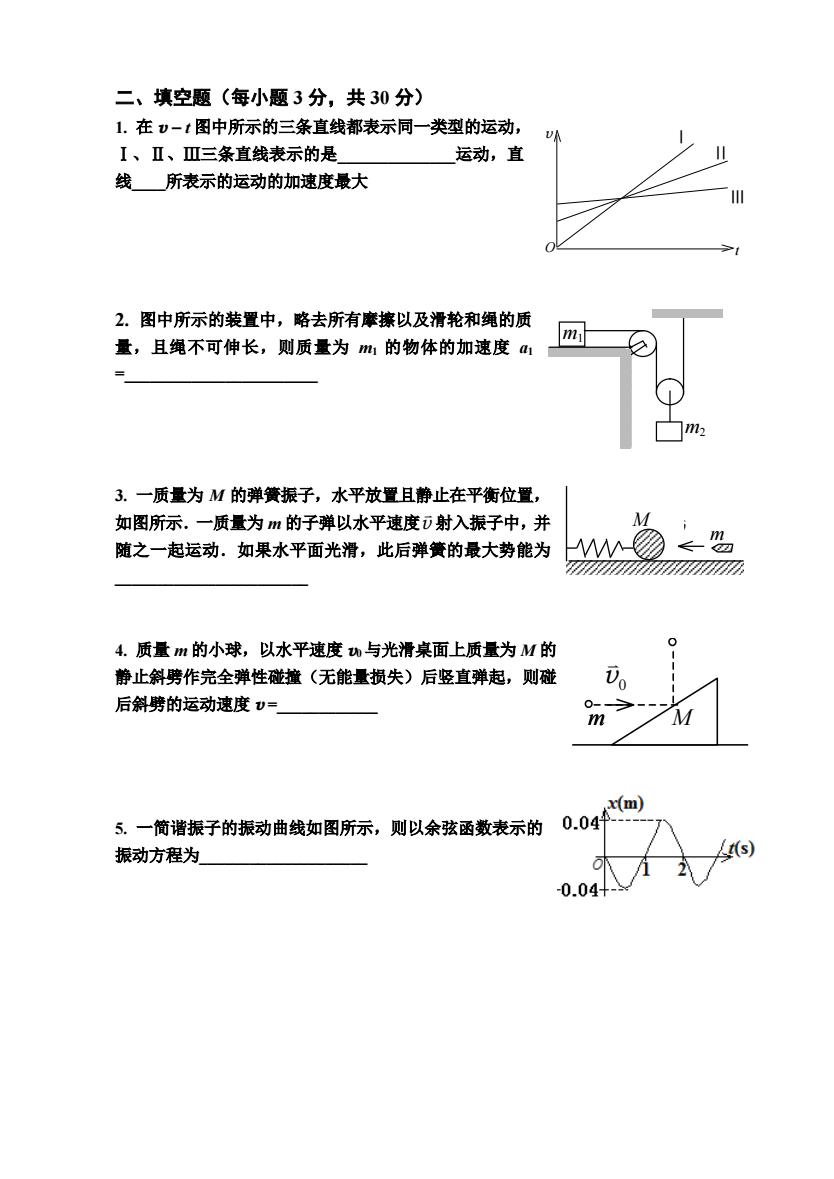
图中所示的装置中,略去所有摩擦以及滑轮和绳的质 二、填空题(每小题 3 分,共 30 分) 1. 在 v t 图中所示的三条直线都表示同一类型的运动, Ⅰ、Ⅱ、Ⅲ三条直线表示的是______________运动,直 线____所表示的运动的加速度最大 2. 量,且绳不可伸长,则质量为 m1 的物体的加速度 a1 =_______________________ 3. 一质量为 M 的弹簧振子,水平放置且静止在平衡位置, 如图所示.一质量为 m 的子弹以水平速度v 射入振子中,并 随之一起运动.如果水平面光滑,此后弹簧的最大势能为 _______________________ 4. 质量 m 的小球,以水平速度 v0与光滑桌面上质量为 M 的 静止斜劈作完全弹性碰撞(无能量损失)后竖直弹起,则碰 后斜劈的运动速度 v =____________ 5. 一简谐振子的振动曲线如图所示,则以余弦函数表示的 振动方程为____________________ v m M m M v0 Ⅰ Ⅱ Ⅲ O t v m1 m2

6.在驻波中,两个相邻波节间各质点的振动相位 (填“相同”或“相反"”) 7.一根长,质量为m的均质细杆可绕通过0点的 13 水平光滑轴在竖直平面内转动,则杆的转动惯量 I= (转轴过杆质心时转动惯量为 1 2B) 8.一静止均质细棒,长为L,质量为M,可绕其左 端点0在光滑水平面内转动,转动惯量为上ML2,一 AV 质量为m,速度为V的子弹在水平面内沿与棒垂直 俯视图 方向射入棒的自由端若子弹穿过棒后速率变为」V, 则棒的角速度为 9.宇宙飞船相对于地面以速度)作匀速直线飞行,某一时刻飞船头部的宇航员向 飞船尾部发出一个光讯号,经过△飞船上的钟)时间后,被尾部的接收器收到,则 由此可知飞船的固有长度为(c为真空中光速) 0.波源位于x=-1处,其振动方程为y0.5cos2π+此波源产生的波无吸 收地分别向x轴正、负方向传播,波速=2。则向x轴正向传播的波动方程为 y1= ,向x轴负向传播的波动方程为 y2=
6. 在驻波中,两个相邻波节间各质点的振动相位____________(填“相同”或“相反”) 7. 一根长 l,质量为 m 的均质细杆可绕通过 O 点的 水平光滑轴在竖直平面内转动,则杆的转动惯量 I=____________(转轴过杆质心时转动惯量为 12 1 ml2) 8. 一静止均质细棒,长为 L,质量为 M,可绕其左 端点 O 在光滑水平面内转动,转动惯量为 3 1 ML2,一 质量为 m,速度为 V 的子弹在水平面内沿与棒垂直 方向射入棒的自由端。若子弹穿过棒后速率变为 2 1 V, 则棒的角速度为__________ 9. 宇宙飞船相对于地面以速度 v 作匀速直线飞行,某一时刻飞船头部的宇航员向 飞船尾部发出一个光讯号,经过t(飞船上的钟)时间后,被尾部的接收器收到,则 由此可知飞船的固有长度为________ (c 为真空中光速) 10. 波源位于 x= -1 处,其振动方程为 y=0.5 cos(2 t+ 3 ),此波源产生的波无吸 收地分别向 x 轴正、负方向传播,波速 u=2。则向 x 轴正向传播的波动方程为 y1=_______________________ , 向 x 轴 负 向 传 播 的 波 动 方 程 为 y2=_______________________

三、计算题(每小题10分,共40分) 1.设有两个参照系S和S”,它们的原点在0和t=0时重合,且S系的z轴分别与 S'系的xy'轴重合。有一事件发生在S系中t=7.0X108s,x=65m,y=0,z=0处。 若S'系相对于S系以速率-0.6c沿x轴正方向运动,求该事件在S系中的时空坐标 (光速c=3×108m/s) 2.如图所示,一平面简谐波沿x轴正方向传播,波由P点反射, 入射 有半波损失,OP=3九4,DP=26。在t=0时,坐标原点0处质点的 合振动是经过平衡位置向负方向运动。求D点处入射波与反射 反射 波的合振动方程。(设入射波和反射波的振幅皆为A,频率为y。) 3.如图所示,质量分别为m和M的两木块由动度系数为k的弹簧相连,静止地放在光 滑水平地面上。质量为的子弹以水平初速度%射入木块,设子弹射入过程时间极短, 求弹簧的最大压缩长度 mo 4.一轻绳绕过一定滑轮,滑轮轴光滑,滑轮半径为R,质量为M/2, 绳子的A端有一质量为M的人抓住了绳端, 而在绳的另一端B系了一质量为。M的重物,如图.设人从静止 开始相对于绳匀速向上爬时,绳与滑轮间无相对滑动,求B端重 物上升的加速度?(滑轮对轴的转动惯量J=MR2/4) B
绳子的 坐标原点O 点处入射波与反射 三、计算题(每小题 10 分,共 40 分) 1. 设有两个参照系 S 和 S',它们的原点在 t=0 和 t'=0 时重合,且 S 系的 xyz 轴分别与 S'系的 x'y'z' 轴重合。有一事件发生在 S'系中 t'=7.0×10-8 s,x'=65 m,y'=0,z'=0 处。 若 S'系相对于 S 系以速率 V=0.6c 沿 x 轴正方向运动,求该事件在 S 系中的时空坐标. (光速 c=3×108m/s) 2. 如图所示,一平面简谐波沿 x 轴正方向传播,波由 P 点反射, 有半波损失,OP = 3 /4,DP= /6。在t = 0 时, 处质点的 合振动是经过平衡位置向负方向运动。求 D 波的合振动方程。(设入射波和反射波的振幅皆为 A,频率为。) 3. 如图所示,质量分别为 m 和 M 的两木块由劲度系数为 k 的弹簧相连,静止地放在光 滑水平地面上。质量为 m0的子弹以水平初速度 v0射入木块,设子弹射入过程时间极短, 求弹簧的最大压缩长度 4. 一轻绳绕过一定滑轮,滑轮轴光滑,滑轮半径为 R,质量为 M / 2, A 端有一质量为 M 的人抓住了绳端, 而在绳的另一端 B 系了一质量为 2 1 M 的重物,如图.设人从静止 开始相对于绳匀速向上爬时,绳与滑轮间无相对滑动,求 B 端重 物上升的加速度?(滑轮对轴的转动惯量 J=MR2 / 4 ) O P B C x 入射 反射 D O B A

答案 一、选择题 BCDCC CCDBA 二、填空题 1.匀加速直线 I 2、 2m28 4m1+m2 m'v2 3. 2(M+m) 4.mvo M 5.x=0.04cos(t+号) 6.相同 1 79 8.3mV/2ML 9.c1 2 10.y1=0.5c0s(2πt-x 3 y1=0.5c0s(2πt+x+-π) 3
CDCC CCDBA 答案 一、选择题 B 二、填空题 1. 匀加速直线 Ⅰ 2. 1 2 2 4 2 m m m g 3. 2( ) 2 2 M m m v 4. v0 M m 5. ) 2 1 x 0.04cos(t 6. 相同 7. 8. 3mV/2ML 9. ct 10. ) 3 2 y1 0.5cos(2t x ) 3 4 y1 0.5cos(2t x

三、计算题 1、解由洛仑兹逆变换式,该事件在S系中的时空坐标为 x+vt_65+0.6×3×108×7.0×108 X= =97(m) V- - y=y'=0 z=z'=0 +x 7.0x108+0.6×65 3x10=2.5×107s -- 2.解:选O点为坐标原点,设入射波表达式为: y=Acos[2π(M-x/)+] P+OP-X)+中+ 则反射波的表达式是: h=Acos[2π(H- 合成波表达式(驻波)为:y=2Acos(2x/)cos(2πM+) 在1=0时,x=0处的质点=0,(⊙,/)<0,故得: 、1 因此,D点处的合成振动方程是: y=2Ac0s(2m3/4-2/6。 c0(254sim2x
OP 三、计算题 2. 解:选 O 点为坐标原点,设入射波表达式为: cos[2 ( / ) ] y1 A t x 则反射波的表达式是: cos[2 ( ) ] 2 OP x y A t 合成波表达式(驻波)为: y 2Acos(2x /)cos(2t ) 在 t = 0 时,x = 0 处的质点 y0 = 0, (y0 / t) 0,故得: 2 1 因此,D 点处的合成振动方程是: ) 2 )cos(2 3 / 4 / 6 2 cos(2 y A t 3Asin 2t

3、解 取地面编老系,子弹与木块m碰撞过程中,动最守恒,于是 movo =(mo +m)vio 式中yo是碰后(m+m)的速度。故 () 加。+m 取(m。十m)、M和弹簧为研究系统,则隧撞后系统的机械能守恒,动量守恒。当弹簧达 到最大压缩长度时x:(m。+m)与M的速度相同,设为”,由机械能守恒,得 m+-m+m+0+号起 (2) 由动量守恒,得 mo'o=(m。+m+M)y (3) 联立式1)、(2)、(3),解得最大压缩长度为 M Xm=movo Y (mo +mX(mo +m+M)k 4.解:受力分析如图所示 设重物的对地加速度为a,向上.则绳的A端对地有加速度a向下, 人相对于绳虽为匀速向上,但相对于地其加速度仍为α向下 T 2分 根据牛顿第二定律可得: 对人: Mg-T2=Ma ① Mg Mg 1 对重物: I-,Ms=亏Ma ② 根据转动定律,对滑轮有 (T-TR=JB=MR2B/4 ③ 因绳与滑轮无相对滑动, a=BR ④ ①、②、③、④四式联立解得 a=2g/7
4. 解:受力分析如图所示. 设重物的对地加速度为 a,向上.则绳的 A 端对地有加速度 a 向下, 人相对于绳虽为匀速向上,但相对于地其加速度仍为 a 向下. 2 分 根据牛顿第二定律可得: 对人: Mg-T2=Ma ① 对重物: T1- 2 1 Mg= 2 1 Ma ② 根据转动定律,对滑轮有 (T2-T1)R=J=MR2 / 4 ③ 因绳与滑轮无相对滑动, a=R ④ ① 、②、③、④四式联立解得 a=2g / 7 O B Mg T2 T1 Mg 2 1 a a