西安电子科技大学：《大学物理》课程教学讲义（下）10-1 库仑定律、静电场

静电场 第1节库仑定律 fx婴，/=g 90 q对g:子=k9g.日 9对q:子=-f,k≈9×10Nm21C2 k=1,6:真空介电常数，6≈885x10C2N-m 4元e0 19 4π6r 第2节 电场和电场强度 9台电场台2 一、 电场强度 试验电荷9。：(1)电量很小，(2)体积很小 1、9o,不同位置，于19。一般不同 2、90,96,96,…，同一位置，了，了，”， f1qo=-'1g%=f"1g6=… ∫19。与试验电荷无关仅与电场中位置有关 定义：电场强度E=f1q。,SI:N1C DE关7，关品 (2)E与q的正、负无关 (3)点电荷qo:于=9E 二、电场强度的计算 1、点电荷的电场 7=,199.2 4πEor2r E=子14o4π6or2r E= 19 4π6or 球对称电场

1 静 电 场 第 1 节 库仑定律 ， ， 2 0 r qq f  2 0 r qq f  k f   q r q0 f q 对q0 ： r r r qq f k     2 0 q0 对q ： f f ，      9 2 2 k  910 Nm /C ， ：真空介电常数， 4 0 1  k  0  12 2 1 2 0 8.85 10       C N m r r r qq f     2 0 4 0 1  第 2 节 电场和电场强度 q1 电场  q2 一、电场强度 试验电荷q0 ：（1）电量很小，（2）体积很小 1、 q0 ，不同位置， f / q0 一般不同  2、 q0 ,q0  ,q0 ,，同一位置，     f , f , f ,     f / q0  f / q0   f / q0   f / q0 与试验电荷无关仅与电场中位置有关  定义：电场强度 E f / q0 ，SI：    N /C （1） E f ，    0 1 q E   （2） E 与 的正、负无关  q0 （3）点电荷q0 ： f q E    0 二、电场强度的计算 1、点电荷的电场 r r r qq f     2 0 4 0 1  f = ， 0 E f / q    r r r q   2 4 0 1  r 0 q 2 4 0 1 r q E   q q  0 q  0 球对称电场 r

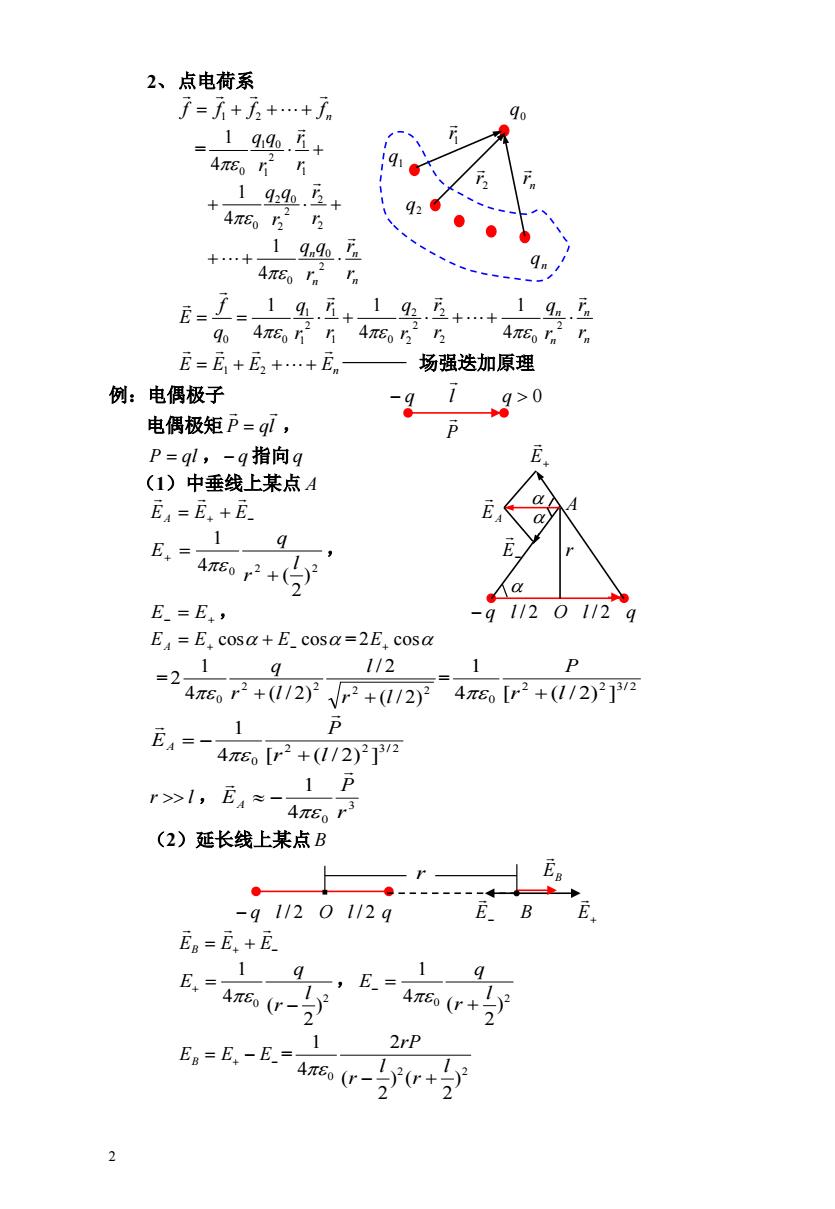
2、点电荷系 于-元+方+…+ 9o =199.1+ 4π60r2片 1446.2+ 4πE05互 +…+ 19n4.五 4π6rn2 E-王-14互+19.互++ 19m. 904π6片14π60322 4πEo In In E=E,+E2+…+En 场强迭加原理 例：电偶极子 >0 电偶极矩P=ql, P=ql,-q指向q E (1)中垂线上某点A E=E.+E E E,= 1 E 480r2+(2 E=E,, -91120112g E=E.cosa+E_cosa=2E.cosa -2、1 1/2 1 P 4π6r2+(112)2VF2+(112)24π6[2+(I12)2]2 P EA二一 1 4π6[r2+(112)2]32 r>1,E4-4P] (2)延长线上某点B ● -91/2O112qE.BE En=E.+E 19 E.=(r -,E= 9 12 4π0 E=6.-m-0+ 2rP 2

2 2、点电荷系 n f f f f      1  2   0 q =   1 1 2 1 1 0 4 0 1 r r r q q      2 2 2 2 2 0 4 0 1 r r r q q   2 q n n n n r r r q q    2 0 4 0 1  n q n n n n r r r q r r r q r r r q q f E               2 2 0 2 2 2 2 1 0 1 2 1 1 0 0 4 1 4 1 4 1    E E E En 场强迭加原理       1  2   例：电偶极子  q l  q  0 电偶极矩 P ql ，    P  ql ， q 指向q E  （1）中垂线上某点 A EA  E  E    EA  ， 2 2 0 ) 2 ( 4 1 l r q E     E  r ， E  E  q l / 2 O l / 2 q EA  E cos  E cos = 2E cos = = 2 2 2 2 0 ( / 2) / 2 4 ( / 2) 1 2 r l l r l q    2 2 3/ 2 0 4 [ ( / 2) ] 1 r l P   2 2 3/ 2 0 4 [ ( / 2) ] 1 r l P EA       r  l ， 3 4 0 1 r P EA      （2）延长线上某点 B  q l / 2 O l / 2 q E  B E  EB  E  E    ，2 0 ) 2 ( 4 1 l r q E     2 0 ) 2 ( 4 1 l r q E     EB  E  E = 2 2 0 ) 2 ) ( 2 ( 2 4 1 l r l r rP     q1 1r 2r nr  P  EB r  A

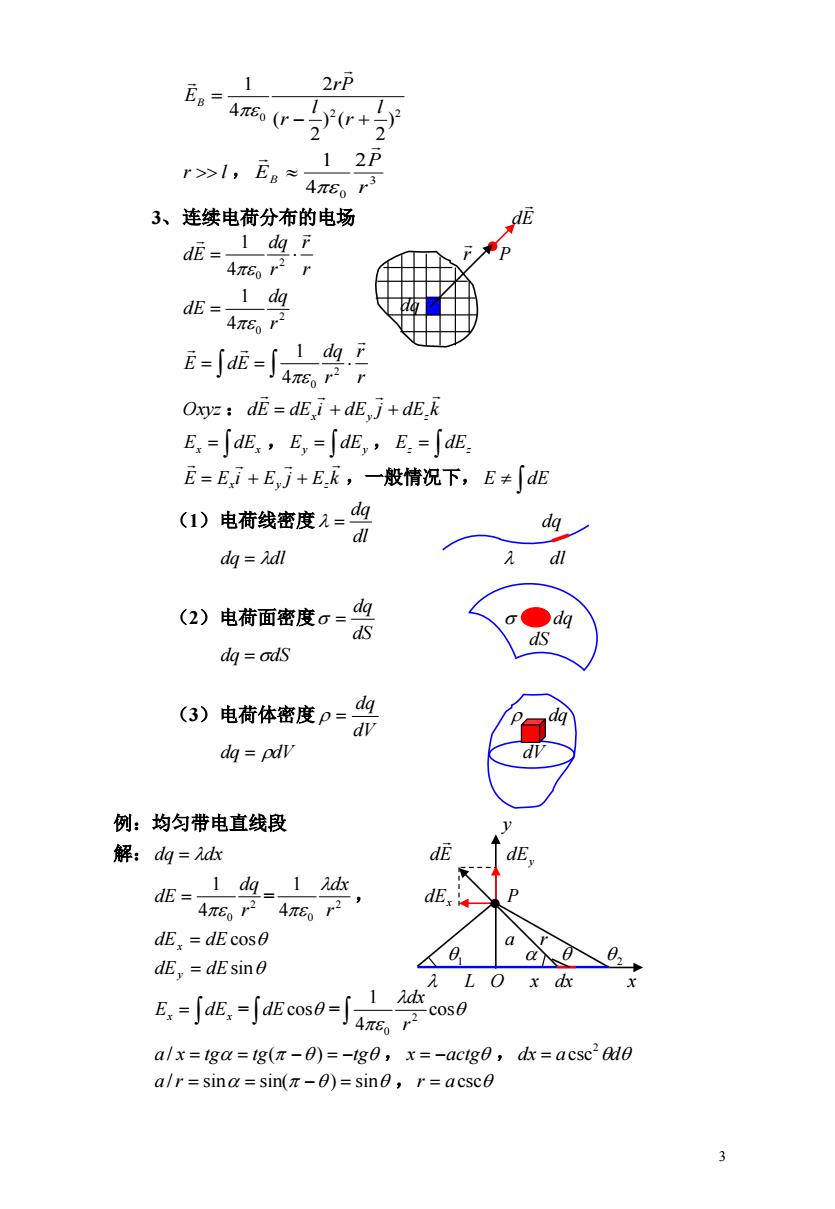
EB 1 2rP 46(-r+ r>1,E≈ 12P 4πE。r3 3、连续电荷分布的电场 dE=-1 dg r 4πEor2r dE=-1 dq 4π6r2 =∫=∫购 4π8。r2r Oxyz:dE=dE i+dE j+dE.k E=∫d，E,=∫d,，E=∫d E=E,i+E,j+ER，一般情况下，E≠「dE (1)电荷线密度1= dl dq Adl dl (2)电荷面密度。= o●dg ds dg ods (3)电荷体密度p= dq dy dq pav d 例：均匀带电直线段 解：dg=dc dE E= dg 1 d 4n6,246r2, dE,dE cos0 dE,=dEsin LOxd E-e-Ea-可a0 a/x=ga=g(π-θ)=-g0，x=-actg0,dk=acsc20 a/r=sina=sin(-0)=sine,r=acsc0 3

3 2 2 0 ) 2 ) ( 2 ( 2 4 1 l r l r rP EB       r  l ， 3 0 2 4 1 r P EB     3、连续电荷分布的电场 dE  r r r dq dE     2 4 0 1  r P 2 4 0 1 r dq dE        r r r dq E dE    2 4 0 1  Oxyz ：dE dE i dE j dE k x y z        Ex   dEx ， Ey   dEy ，  Ez  dEz E Exi Ey j Ezk ，一般情况下，         E  dE （1）电荷线密度 dl dq   dq dq  dl  dl （2）电荷面密度 dS dq    dq dq  dS （3）电荷体密度 dV dq    dq dq  dV dV 例：均匀带电直线段 y 解：dq  dx dE  dEy = ， 2 4 0 1 r dq dE   2 0 4 1 r dx  dEx P dE dE cos x  a r dEy  dE sin = =  Ex  dEx  dEcos    cos 4 1 2 0  r dx a / x  tg  tg(  )  tg ， x  actg ，dx a d 2  csc a /r  sin  sin(  )  sin ，r  acsc dS  L O x dx x 1    2 dq

品 cosede 4πEaa 元_(sin0,-sin8） 4π6a E,=∫d,=∫dEsin0= 4π6a8 (cos0,-cos0:) 4π6oa E=Ei+E,] E↑↑↑↑ 讨论：1不变，L→0 81=0,02=π E=0 E,= 2π6oa E= 2π8oa 轴对称电场 例：均匀带电细圆环 解：dg=adl,(=9) dl 2πR dE' dE= 1 dg 1 idl 4π6r2 4n6r2’ dE dE,dE cosa dE --dE dE =dE sina dl"'dl 由于对称性，E=0 E=E=∫ac,=∫Ecosa=∫，1a 4760c0S 4cosd dl-coscom-gcosa 4n6,2 1 gx E=4r,(K+R27 讨论：（1)x=0,圆心处，E=0 (2)x>R,E≈，1马 4π60x 4

4  =      cos csc csc 4 1 2 2 2 0 a a d Ex    2 1 cos 4 0       d a = (sin sin ) 4 2 1 0      a = =  Ey  dEy  dEsin  2 1 sin 4 0       d a = (cos cos ) 4 1 2 0      a E E i E j x y      E  讨论： 不变， L    1  0 ， 2   Ex  0 a Ey 2 0    a E 2 0    轴对称电场 例：均匀带电细圆环 解：dq  dl ，（ ） R q   2  dl = ， 2 4 0 1 r dq dE   2 4 0 1 r dl  O x dEx x dE dEcos x  q dE dE  dE  dEsin  dl  dl 由于对称性， E  0  = =  E  Ex  dEx  dEcos    cos 4 1 2 0  r dl =  dl = = ， ， r 2 4 0 cos    R r     2 4 cos 2 0 2 4 0 cos r q   r x cos  2 2 r  x  R 2 2 3 / 2 0 4 ( ) 1 x R qx E    讨论：（1） x  0，圆心处， E  0 （2） x  R ， 2 4 0 1 x q E     P dE   R r

例：均匀带电圆盘 求：轴线上E dr 解：dB=2mdr dE dq odS =o2mdr dE=_ xdg 4π6(x2+r2)32 =_1 xo2mdr rdr 46(6x2+r2)26(x2+r2) --宽停n rdr 1 d(x2+r2) = 1 R 0212132=28-x2+3p 280 280 10 1 +)=g 2√x2+R2x (1- 260 r+R 讨论：o不变，R→0，无限大均匀带电平面，E= 260 g>0 <0 例：细圆环(R) 元=，cosB dl 求：圆心处E R A☑=c0s8 解：dl=RdO dg =Adl=cosORde de= dq cosede d 4πE,R2 4π6R dE,=-dE cos,dE,=-dEsin &,-jE,-Ew0- ocos2@do =-名[l+cos20d0=- 4π6RJ02 46R E,-j亚，-jEm0一-4Rm0mw=0 E=-4 46R 5

5 例：均匀带电圆盘 求：轴线上 E   dr 解：dS  2rdr R r dE  dq  dS   2rdr x x 2 2 3 / 2 0 4 ( ) 1 x r xdq dE    = = 2 2 3 / 2 0 ( ) 2 4 1 x r x rdr     2 2 3 / 2 0 2 (x r ) x rdr         R x r x rdr E dE 0 2 2 3/ 2 0 2 ( )  = 0 ) 1 ( ( ) 2 ( ) 2 1 2 2 2 0 0 2 2 3/ 2 2 2 0 R x r x x r d x r x R           = (1 ) 2 ) 1 1 ( 2 2 2 0 2 2 0 x R x x R x x           讨论： 不变， R   ，无限大均匀带电平面， 0 2  E    0   0 E  例：细圆环（ R ）   0 cos 求：圆心处 E  解：dl  Rd dq  dl  0 cosRd R d R dq dE 0 0 2 0 4 cos 4        dEx  dEcos ，dEy  dEsin = =  Ex  dEx   dEcos      d R 2 2 0 0 0 cos 4   = =         2 0 0 0 2 1 cos2 4 d R 0R 0 4   = = =0  Ey  dEy   dEsin        2  0 0 0 cos sin 4 d R i R E   0 0 4    O P d R x dEy dEx  dE  dl   0 cos O y