西安电子科技大学：《大学物理》课程教学讲义（上）05 动量、冲量、动量定理

第4节动量冲量 动量定理 一、质点的动量定理 F=ma=m- 亚，F=dm dt F合外为 定义：质点动量P=m下方向沿的方向 大小P=mV 单位：kgms,量纲：MLT-l F=dp 质点的动量定理（微商形式） dP Fdt, Fd:合外力的元冲量 质点动量定理（微分形式） aP-f→A=乃-月=F动 定义：冲量7=Fd,失量，单位：Ns,量纲：MT- INs =1kgms 注意： 1、冲量的大小1==心Fd≠Fd 2、合力F=F+2+…+Fn的冲量 7-fd=心(+月++)d =fd+fd+…+f.d=i+i2++i。 等于每个力冲量的矢量和 3、如果F是恒力，则7=d=F42-1)=Pt ī与F同方向，一般情况下，了与F(变力)方向不同 4力的平均值：厅 -4 i=∫Fd=F4,-4)=FA1,1与F同方向 Ap=7=∫Fd (积分形式) AP=i-FA1→F=A0 (差商形式) △1 1

1 第 4 节 动量 冲量 动量定理 一、质点的动量定理 V  F  = m a  = m dt dV  ， F  = dt d(mV)  L 定义：质点动量 P  =m V     P = mV V 大小 方向沿 的方向  单位： −1 kgms ，量纲： −1 MLT F  = dt dP  质点的动量定理（微商形式） dP Fdt   = ， Fdt  ：合外力的元冲量 质点动量定理（微分形式）   = 2 1 2 1 t t P P dP Fdt      P   = P2 P1   − =  2 1 t t Fdt  定义：冲量 I  =  2 1 t t Fdt  ，矢量，单位： Ns ，量纲： −1 MLT 1 1 1 − Ns = kgms 注意： 1、 冲量的大小 I = I  =  2 1 t t Fdt    2 1 t t Fdt 2、 合力 F F F Fn      = 1 + 2 + + 的冲量 I  =  2 1 t t Fdt  =  + + + 2 1 ( ) 1 2 t t F F Fn dt     =  2 1 1 t t Fdt  +  2 1 2 t t F dt  +  + 2 1 t t Fndt   = 1 I  + 2 I  + n I  + 等于每个力冲量的矢量和 3、 如果 F  是恒力，则 I  =  2 1 t t Fdt  = ( ) 2 1 F t − t  = Ft  I  与 F  同方向，一般情况下， I  与 F  （变力）方向不同 4、 力的平均值： 2 1 2 1 t t Fdt F t t − =    I  =  2 1 t t Fdt  = ( ) 2 1 F t − t  = Ft  ， I  与 F  同方向 P   = I  =  2 1 t t Fdt  （积分形式） P   = I  = Ft   F  = t P    （差商形式） F  合外力 m

p=mV,P=mV,,P=mVs,P:=mV: i-f心d,1-心F,1,=F,h,L.-rh △P=i=fd AP=1=Fdi,AP,=1=F,di,AP.=1.=Fd △1 △t △1 △t F=dp dt d dt dp=Fdt,dp =F dt,dPy=Fydt,dP.=F.dt 一维直线运动 P=mV,I=Fd,AP=1=Fd T所，P=fFh 动量定理只适用于惯性系 例：m=1kg的质点从O点出发作R=2m 的圆周运动，运动方程s=号2m 求：41=√2s~2=2s合外力的冲量7 B 解：速率V==m 1=V2s,s=π(m),位于A点 V4=V2π，P4=√2π，方向← t2=2s,5=2π（m),位于B点 V。=2π，PB=2π，方向↓ 7=△P=PB-P4, I=√P+P=V6π(Ns), i=△P g0=2=2m- P。2π2 ,0=35.3 二、质点系的动量定理 m,:合外力后，合内力f 合力E+f dP =(F+f)dt Fdt+f;dt i=1,2,…n ∑dp=∑F,d+∑j,dh d(∑P)=(∑E)d+(∑f)d 2

2 P  = m V  ， Px =m Vx， Py =m Vy ， Pz =m Vz I  =  2 1 t t Fdt  ， x I =  2 1 t t Fxdt ， y I =  2 1 t t Fydt ， z I =  2 1 t t Fzdt P   = I  =  2 1 t t Fdt  Px= x I =  2 1 t t Fxdt ， Py = y I =  2 1 t t Fydt ， Pz = z I =  2 1 t t Fzdt F  = t P    ， Fx = t Px   ， Fy = t Py   ， Fz = t Pz   F  = dt dP  ， Fx = dt dPx ， Fy = dt dPy ， Fz = dt dPz dP Fdt   = ， dP F dt x = x ， dP F dt y = y ， dP F dt z = z 一维直线运动 P = mV ，  = 2 1 t t I Fdt ，   = = 2 1 t t P I Fdt t P F   = ， dt dP F = ， dP = Fdt 动量定理只适用于惯性系 y 例： m =1 kg 的质点从 O 点出发作 R =2 m VA  的圆周运动，运动方程 2 2 1 s = t (m) R 求： t 2s ~ t 2s 1 = 2 = 合外力的冲量 I  B O x 解：速率 t dt ds V = =  t 2s 1 = ， s =  （ m ），位于 A 点 VB  VA = 2 ， PA = 2 ，方向  t 2s 2 = ， s = 2 （ m ），位于 B 点 VB = 2 ， PB = 2 ，方向  PA  I  = P   = PB PA   − ， 2 2 PA PB I = + = 6 (Ns) ， I  = P    2 2 2 2 = = =    B A P P tg ，   = 35.3 PB  二、质点系的动量定理 mi ：合外力 Fi  ，合内力 i f  Fi  合力 Fi  + i f  dP F f dt F dt f dt i i i i i      = ( + ) = + mi i f  i = 1,2, n dPi =  F dt i  +  f dt i  ( ) d Pi  = F dt i ( )  +  f dt i ( )  A

定义：质点系的动量P=∑P=∑m,' F-∑瓦，：质点系受到的合外力。合内力∑，=0 dP=Fd(微分形式) Fd护 (微商形式)，对质点系也成立！ di AP=E-月=∫Fd (积分形式) A=1=FA1→F=△ (差商形式) △1 质点系动量定理只适用于惯性系 例：h=0.5m,流量qm=40kg/s A:V=2m/s向右 求：煤粉对A的作用力 的大小和方向 V=2mls (不计相对传送带 eceeeeeeeeel 静止的煤粉质量) 解：先计算A对煤粉的作用力。设△t(→0)时间内，△m=qm△1 △m落在A上之前V。=√2ghP=△m'。 方向↓ 之后V P=△mV 方向→ AP=P-Po A=VR+p2=△mVg+V严=q△Vg+ △P=p-P, 180=P-v v 0=32.3° P V。V2gh 煤粉对A的作用力与F大小相等方向相反 第5节动量守恒定律 dP Fdt 如果合外力F=0→dp=0→P=C ∑m,厂，=C:动量守恒定律 如果F≠0，F在某一方向的投影为零，则在该方向上动量守恒 cg,F=0,∑m,'x=C 说明：1、动量守恒是指系统动量始终保持不变 2、动量守恒的条件是F=0,不是1=Fd=0 F=0是动量守恒的充要条件 3、内力可以改变个别质点的动量，但不能改变系统的动量 4、在微观世界仍然成立 3

3 定义：质点系的动量 P = Pi   =miVi  F = Fi   ：质点系受到的合外力。合内力  i f  =0 dP Fdt   = （微分形式） F  = dt dP  （微商形式），对质点系也成立！ P   = P2 P1   − =  2 1 t t Fdt  （积分形式） P   = I  = Ft   F  = t P    （差商形式） 质点系动量定理只适用于惯性系 例： h = 0.5m ，流量 q kg s m = 40 / A ： V = 2m/s 向右 求：煤粉对 A 的作用力 的大小和方向 h V = 2m/s （不计相对传送带 A 静止的煤粉质量） 解：先计算 A 对煤粉的作用力。设 t （ →0 ）时间内， m q t  = m m 落在 A 上之前 V0 = 2gh P0 =m V0 方向  之后 V P =m V 方向 → P   = P P0   − ， P  2 2 0 2 2 0 2 2 P = P0 + P = m V +V = qmt V +V  P   = P P0   − F  = t P    ， t P F   =   = 2 2 qm V0 +V =149(N) P0  gh V V V P P tg 0 0 2  = = = ，   = 32.3 煤粉对 A 的作用力与 F  大小相等方向相反 第 5 节 动量守恒定律 dP Fdt   = 如果合外力 F = 0   dP = 0   P C   = miVi = C   ：动量守恒定律 如果 F  0  ， F  在某一方向的投影为零，则在该方向上动量守恒 e.g.， Fx = 0， miVix = C 说明：1、动量守恒是指系统动量始终保持不变 2、动量守恒的条件是 F = 0  ，不是 0 2 1 = =  t t I Fdt   F = 0  是动量守恒的充要条件 3、内力可以改变个别质点的动量，但不能改变系统的动量 4、在微观世界仍然成立 

5、只适用于惯性系 6、内力>>外力且持续时间较短的过程，如爆炸、强烈碰 撞过程，虽有外力，也可使用动量守恒定律 火箭飞行原理 V ,dm V+dv I,m t+dt,m+dm mV =(m+dm)v+dv)+(-dm)(-V,+V+dv) mVmV+mdv dm-V+dmdv+dm-V.-dm-V-dmdv mw+m=0→r=-y0an--y9 V=-ynm=yn,m,v个 mo m m。=m,+m',m,:箭壳及卫星质量，m:然料质量 燃料燃烧完后，m=m V'rs =Vm =y1+四)，四称为质量比 m m. m 由y及m决定 m V≈4kml/s 地球轨道，Vnmx≈8km/s,m/m,=e2-1≈7 目前，m1m,=l15,'x≈11km/s 考虑到地球引力及空气摩擦力，Vx≈7kmls 单级火箭 多级火箭 4

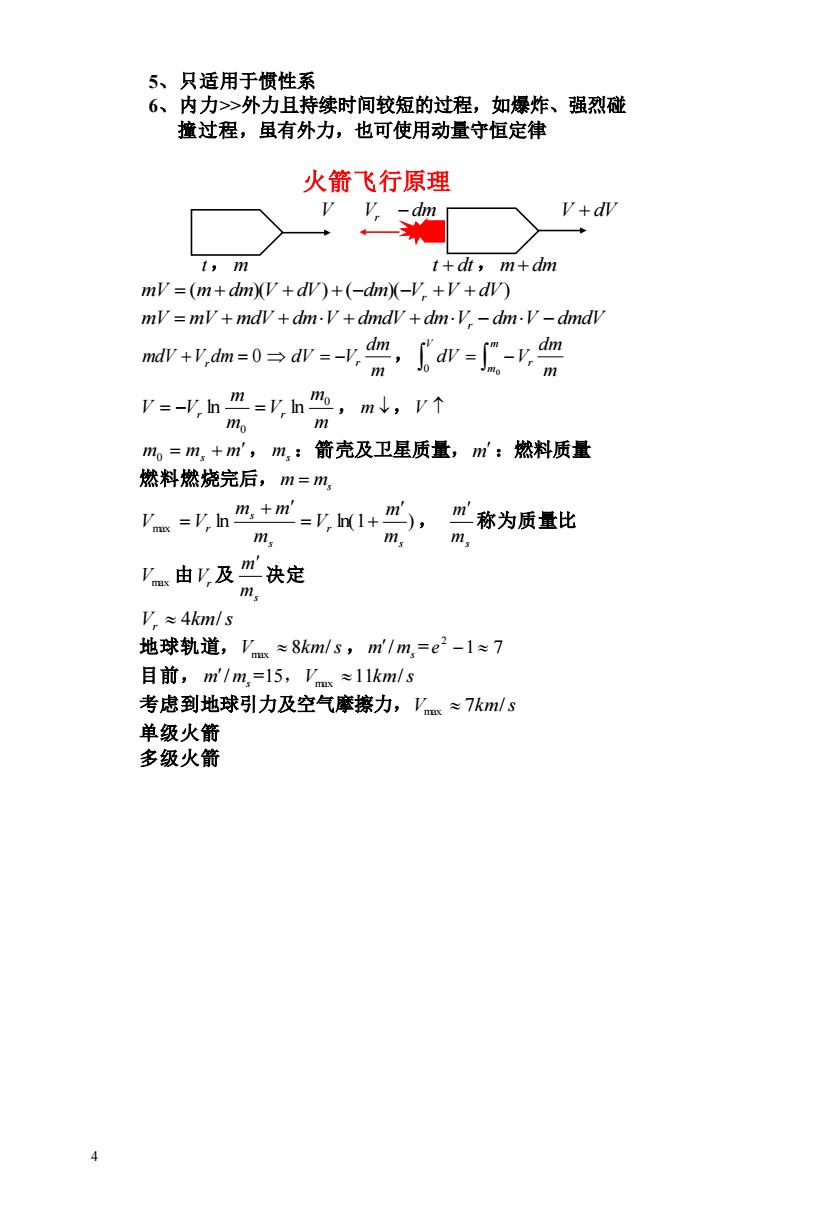
4 5、只适用于惯性系 6、内力>>外力且持续时间较短的过程，如爆炸、强烈碰 撞过程，虽有外力，也可使用动量守恒定律 火箭飞行原理 V Vr − dm V + dV t ， m t + dt ， m+ dm mV (m dm)(V dV) ( dm)( V V dV) = + + + − − r + + mV = mV + mdV + dmV + dmdV + dmVr − dmV − dmdV mdV +V dm = 0 r  m dm dV = −Vr ，   = − m m r V m dm dV V 0 0 m m V m m V Vr r 0 0 = − ln = ln ， m ，V  m = ms + m  0 ， ms ：箭壳及卫星质量， m  ：燃料质量 燃料燃烧完后， m = ms ln ln(1 ) max s r s s r m m V m m m V V  = + +  = ， ms m  称为质量比 Vmax 由 Vr 及 ms m  决定 V km s r  4 / 地球轨道， V 8km/s max  ，m ms / = 1 7 2 e −  目前， m ms / =15，V 11km/s max  考虑到地球引力及空气摩擦力， V 7km/s max  单级火箭 多级火箭