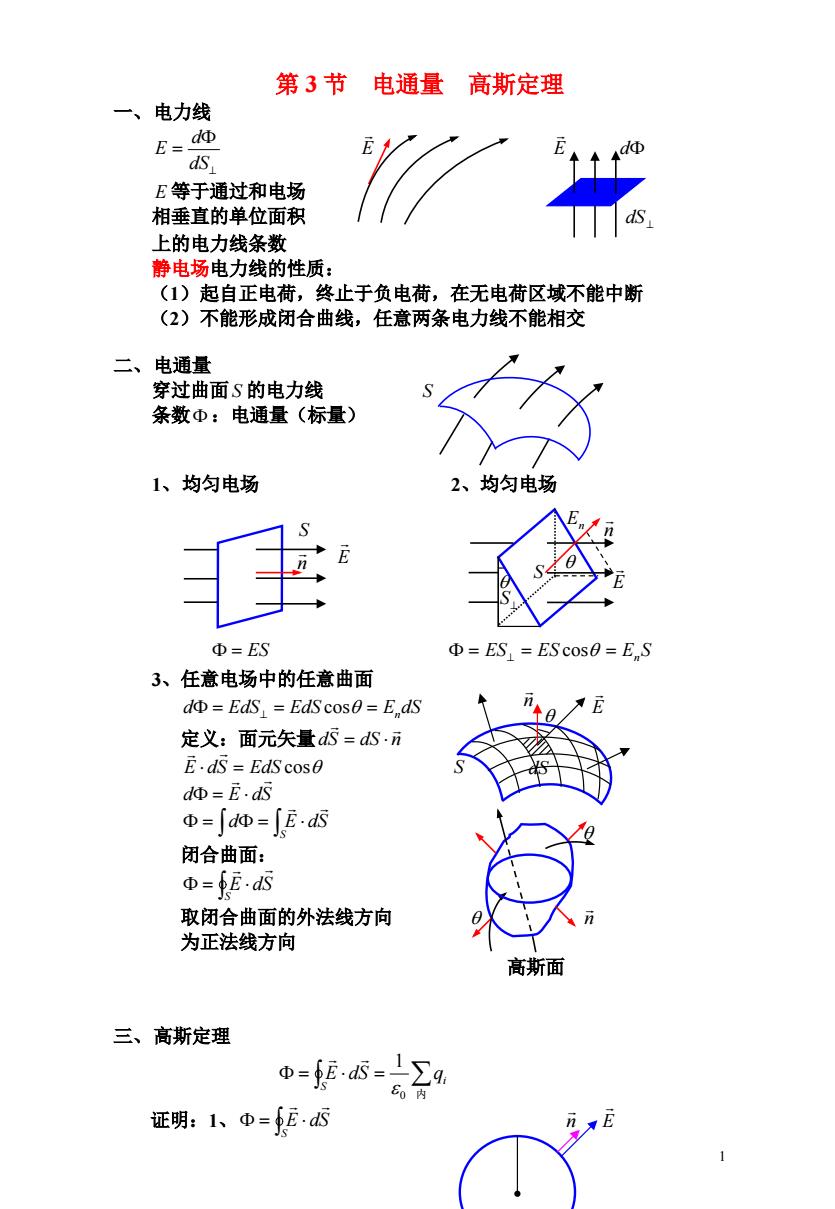
第3节 电通量 高斯定理 一、电力线 E、地 ds E等于通过和电场 相垂直的单位面积 上的电力线条数 静电场电力线的性质: (1)起自正电荷,终止于负电荷,在无电荷区域不能中断 (2)不能形成闭合曲线,任意两条电力线不能相交 二、电通量 穿过曲面S的电力线 条数Φ:电通量(标量) 1、均匀电场 2、均匀电场 Φ=ES Φ=ES,=EScos0=E,S 3、任意电场中的任意曲面 d=EdS EdS cos0=E,dS 定义:面元矢量dS=dS.n E.dS EdS cos0 dΦ=E.dS Φ=∫Φ=E 闭合曲面: Φ=fE 取闭合曲面的外法线方向 为正法线方向 高斯面 三、高斯定理 Φ=fE.5=∑ 60内 证明:1、Φ=E E
1 第 3 节 电通量 高斯定理 一、电力线 dS d E E E d E 等于通过和电场 相垂直的单位面积 dS 上的电力线条数 静电场电力线的性质: (1)起自正电荷,终止于负电荷,在无电荷区域不能中断 (2)不能形成闭合曲线,任意两条电力线不能相交 二、电通量 穿过曲面 S 的电力线 S 条数 :电通量(标量) 1、均匀电场 2、均匀电场 S n E E ES ES ES cos EnS 3、任意电场中的任意曲面 d EdS EdS E dS n cos E 定义:面元矢量dS dS n E dS EdS cos S d E dS S d E dS 闭合曲面: S E dS 取闭合曲面的外法线方向 n 为正法线方向 高斯面 三、高斯定理 内 i S E dS q 0 1 证明:1、 S E dS n E n dS n S S En
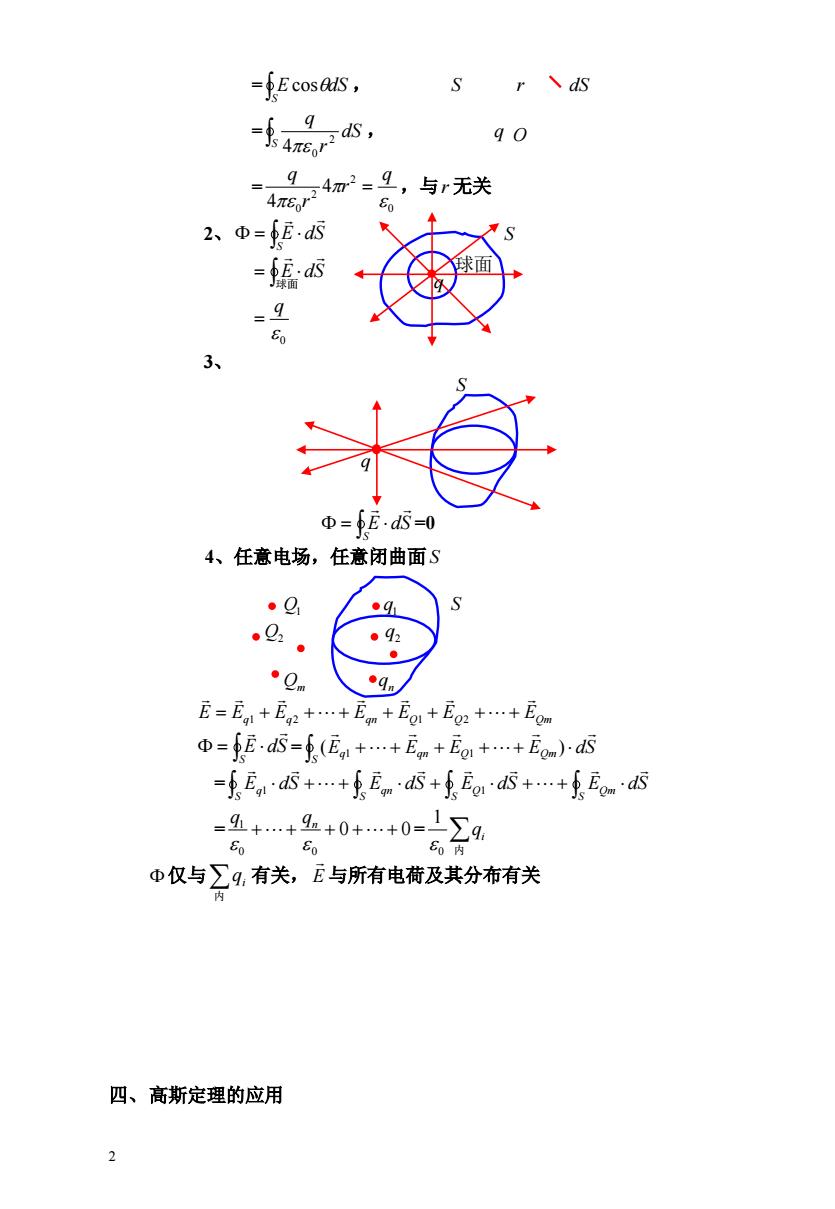
-E cosas, SrdS 90 =,974m2=9,与r无关 4π8r1 2、Φ=fEs =猛a 球面 3、 Φ=fE·d5=0 4、任意电场,任意闭曲面S ·Q 92 ·92 ·0nm ●qn E=E,1+E,+…+En+Eo1+E2+…+Em D=fEd否=f(瓦,+…+En+Eo++E)d西 =f,a++重E,na西+fEo5+…+5EoaS -县++2+0++0-24 Φ仅与∑9,有关,E与所有电荷及其分布有关 四、高斯定理的应用 2
2 = , S E cosdS S r dS = , S dS r q 2 0 4 q = ,与 无关 0 2 2 0 4 4 q r r q r 2、 S E dS S 球面 E dS 0 q 3、 S =0 S E dS 4、任意电场,任意闭曲面 S Q1 q1 S Q2 q2 Qm n q E Eq Eq Eqn EQ EQ EQm 1 2 1 2 = S E dS E E E E dS S q qn Q Qm ( ) 1 1 = E dS E dS E dS E dS S Qm S Q S qn S q 1 1 = 0 0 = 0 0 1 n q q 内 i q 0 1 仅与 有关, 与所有电荷及其分布有关 内 i q E 四、高斯定理的应用 O q 球面 q
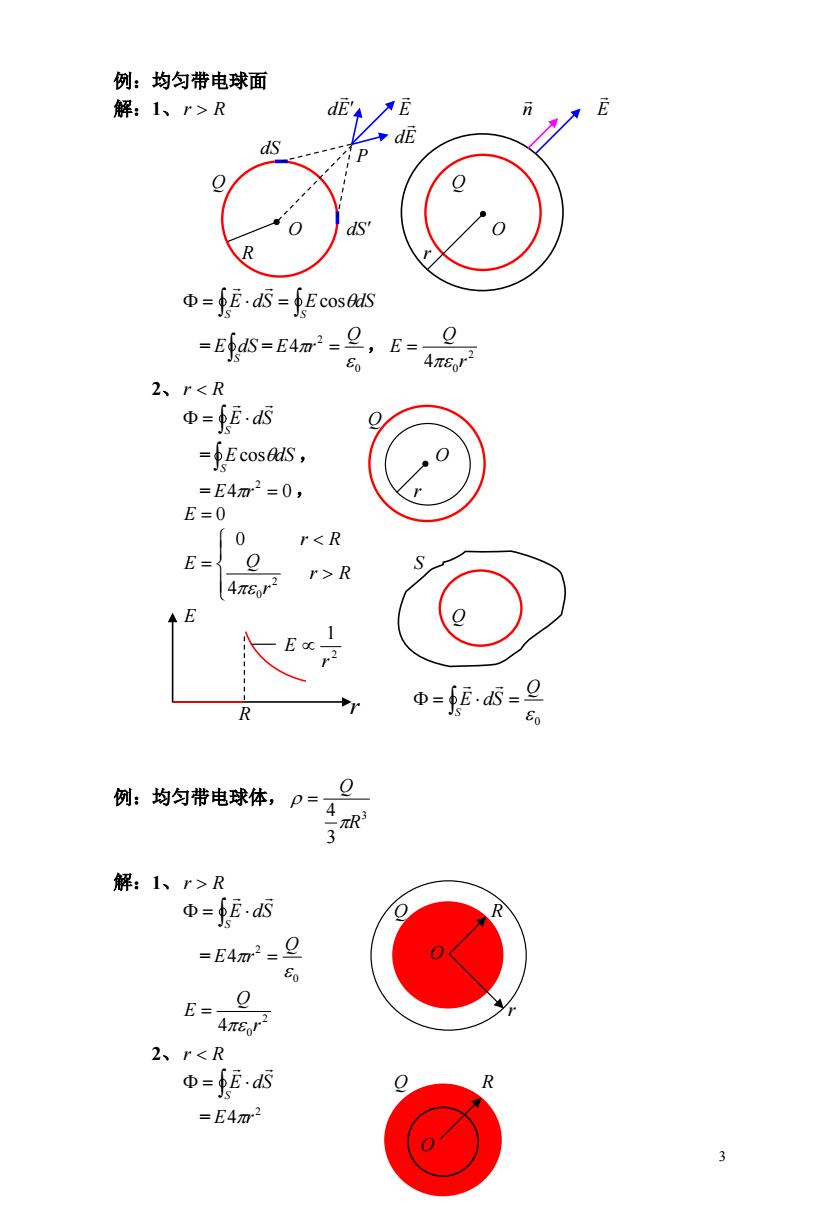
例:均匀带电球面 解:1、r>R de' E E dE ds ds' Φ=fE.s=fEcosais =E4=E4m-2,E= 2、rR E R Φ=fE5=卫 例:均匀带电球体,p= Q 4 R3 3 解:1、r>R Φ=fEs =E4m2= 80 E=4n57 2、r<R Φ=fE R =E4m2
3 例:均匀带电球面 解:1、r R dE E n E dE Q Q O dS O R r S S E dS EcosdS = = , S E dS 0 2 4 Q E r 2 4 0r Q E 2、r R S E dS = , S EcosdS O = 4 0 , 2 E r r E 0 r R r Q r R E 2 4 0 0 S E Q 0 Q E dS S 例:均匀带电球体, 3 3 4 R Q 解:1、r R S E dS Q R = 0 2 4 Q E r 2 4 0r Q E r 2、r R S E dS Q R = 2 E4r R r dS P 2 1 r E O O Q
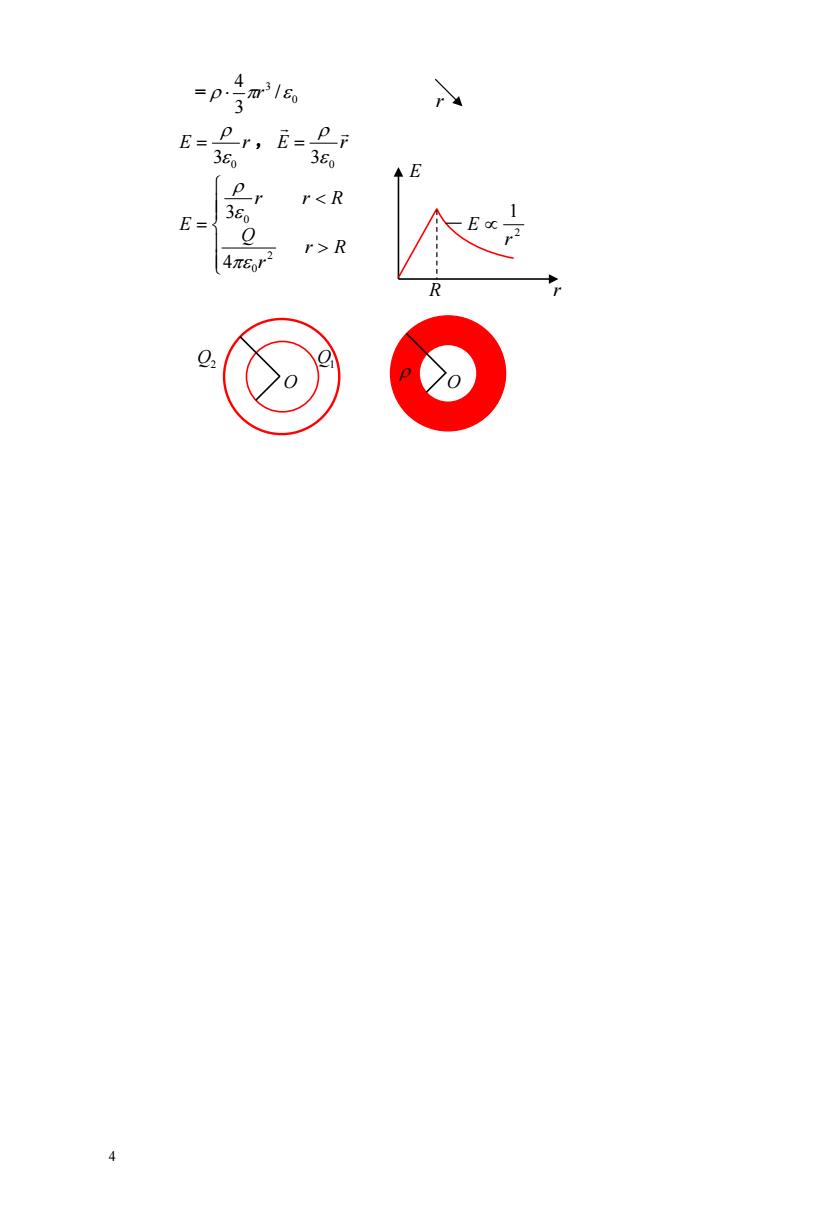
=P. 316 3 E= er, 36 380 (er E rR 4π8or R 02 9 4
4 = 0 3 / 3 4 r E r , 3 0 E r 0 3 r R r Q r r R E 2 0 0 4 3 2 1 r E R r Q2 Q1 O O E r