第6节场强与电势的关系 E、U,U=E.ai 一、等势面 1点电荷,U=,9 4πEoJ 2、无限长均匀带电直线,U=-一 3、无限大均匀带电平面,U=- 260 约定:相邻的两个等势面的电势差都相等 性质: (1)沿等势面移动电荷,电场力作功为零 (2)等势面与电力线处处正交, 电力线的方向为电势降落的方向 1
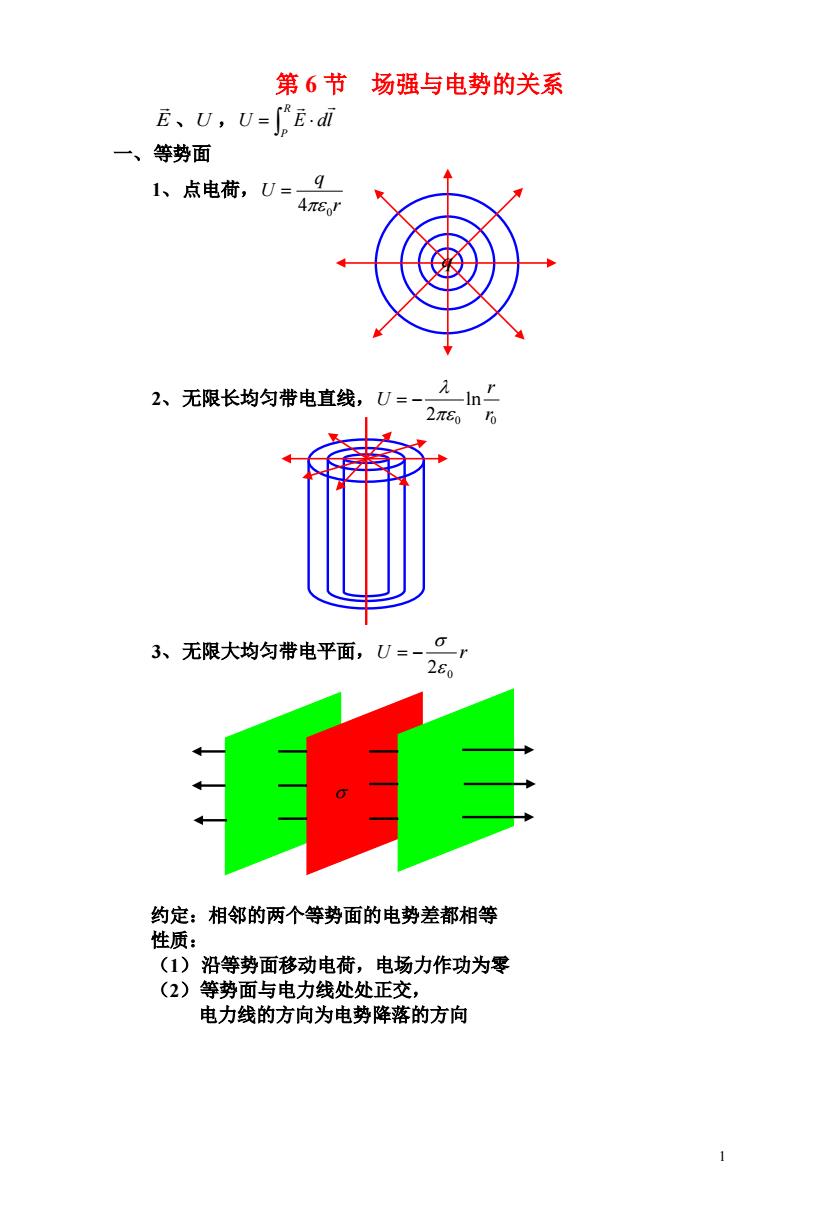
1 第 6 节 场强与电势的关系 E 、 , U R P U E dl 一、等势面 1、点电荷, r q U 4 0 2、无限长均匀带电直线, 0 0 ln 2 r r U 3、无限大均匀带电平面,U r 2 0 约定:相邻的两个等势面的电势差都相等 性质: (1)沿等势面移动电荷,电场力作功为零 (2)等势面与电力线处处正交, 电力线的方向为电势降落的方向 q

证明: (1)Up=Ue A=qoUPo =0 (2)反证法: 设等势面上某点处 E与等势面不正交 9o dl Ecos0 即0≠π Ecos@≠0,dA=qE.di=goEcosedl≠0,矛盾 U,-U。-E.i =Ecosl=∫Ed>0 Up>Uo 二、场强与电势的微分关系 du>0,Un>U 等势面的正法线方向: P 沿电势增加的方向 dn dU >0 PP>PP U+dU dn dl cos0 dudu (方向导数) E U dn dl dU du du cose dl dn/cose dn coss1, d dn 定义:电势梯度VU的方向:电势增加率最大的方向 大小U川-盟 VU-Un dn dA=9oE·d而=9oUAs→9oE(-l)dn=qol[U-(U+dU)】 E(-1)dn=-dU,E= dn E=-VU=- n dn E.0=- dn 2
2 证明:(1) UP UQ S 0 A q0UPQ P Q (2)反证法: 设等势面上某点处 E 与等势面不正交 q0 dl Ecos 即 2 Ecos 0 ,dA q0E dl q0Ecosdl 0,矛盾 Q P P Q U U E dl E = = Q P Ecosdl 0 Q P Edl UP UQ 二、场强与电势的微分关系 U dU 0,UII UI 等势面的正法线方向: 沿电势增加的方向 P3 dU 0 P1P3 P1P2 II U dU dn dl cos 、 (方向导数) dn dU dl dU El I U = = , dl dU dn / cos dU dn dU cos E cos 1, dl dU dn dU 定义:电势梯度U 的方向:电势增加率最大的方向 大小: dn dU U n dn dU U 0 0 P1P2 dA q E dn q U ( 1) [ ( )] q0E dn q0 U U dU E(1)dn dU , dn dU E n dn dU E U 0 0 n l dn dU E l P dn P2 q0 dl 0 l P1 E Q n 0 q

du COs0=_ dn dl al Oxyz:1=i,j,k, aU E.= aU aU E,=- E.= SI:V/m Ox Oy 82 例:均匀带电圆环(q,R)轴线上电势U= q 4r6√x2+R2 求:轴线上E 解:E=-dU =-(x+R)2x gx x4π6。 4π6。(x2+R2)3n 由于对称性,E,=0,E=0 例:电势U=Aln(x2+y2) 求:E 解:E,=-=-4 2x 。x2+2E:=-=0 x+E影12” 例:两个均匀带电球面同心 R/OPP 0 rR 4πEr2 1、r<R U-E.di-Ecosadl cosdcoscos -店品+g8 =g-凸+9+01=g。+,0 4π6RR24πE0R34πER4πER 2、R<r<R2 U-E.di-EcosllEcos+Ecosall
3 l U dl dU dn dU El cos Oxyz :l i j k , , , 0 , , SI:V/m x U Ex y U Ey z U Ez 例:均匀带电圆环(q , R )轴线上电势 2 2 4 0 x R q U 求:轴线上 E 解: = = x U Ex x R x q )( ) 2 2 1 ( 4 2 2 3 / 2 0 2 2 3 / 2 0 4 ( ) 1 x R qx 由于对称性, Ey =0, Ez =0 例:电势 ln( ) 2 2 U A x y 求: E 解: = , = , =0 x U Ex 2 2 2 x y x A y U Ey 2 2 2 x y y A z U Ez 例:两个均匀带电球面同心 Q2 Q1 R1 O P P P R2 解: 2 2 0 1 2 2 1 2 0 1 1 4 4 0 r R r Q Q R r R r Q r R E 1、 R1 r = P U E dl P Ecosdl = + + 1 cos R P E dl 2 1 cos R R E dl 2 cos R E dl = + 2 1 2 0 1 4 R R dr r Q 2 2 0 1 2 R 4 dr r Q Q = ) + = + 1 1 ( 4 0 1 2 1 R R Q 0 2 1 2 1 4 R Q Q 0 1 1 4 R Q 0 2 2 4 R Q 2、 1 R2 R r = = + P U E dl P Ecosdl 2 cos R P E dl 2 cos R E dl

-+号 4πE2 JR24πEr1 =9心-)+9+01=0+,9 4πErR24πER24π6r4πER2 3、r> U="E.di="Ecosll -9号h-9t01-g+Q 4π6。r4πEor4π81 UU R 0, R R 1、rR U= 9+9 4πEr4πEor 静电场小结 库仑定律 高斯定理: fEs=上∑4 0内 场强迭加原理 环路定理: fE.di=0 静电场是有源场,电荷是静电场的场源 静电场是保守场,是引入电势的先决条件 E满足矢量迭加原理,U满足标量迭加原理 U=∫Eal,E=-vU=-Wm dn 4
4 = + 2 2 0 1 4 R r dr r Q 2 2 0 1 2 R 4 dr r Q Q = ) + = + 1 1 ( 4 0 2 1 r R Q 0 2 1 2 1 4 R Q Q r Q 0 1 4 0 2 2 4 R Q 3、 R2 r = P U E dl P Ecosdl = = = + r dr r Q Q 2 0 1 2 4 r Q Q 1 4 0 1 2 r Q 0 1 4 r Q 0 2 4 U R1 R2 r Q2 Q1 R1 O R2 1、r R1 + 0 1 1 4 R Q U 0 2 2 4 R Q 2、 R1 r R2 + r Q U 0 1 4 0 2 2 4 R Q 3、r R2 + r Q U 0 1 4 r Q 0 2 4 静电场小结 库仑定律 高斯定理: 内 i S E dS q 0 1 场强迭加原理 环路定理: 0 L E dl 静电场是有源场,电荷是静电场的场源 静电场是保守场,是引入电势的先决条件 E 满足矢量迭加原理, 满足标量迭加原理 U , R P U E dl n dn dU E U