西安电子科技大学：《大学物理》课程教学讲义（下）10-6 静电场习题课I

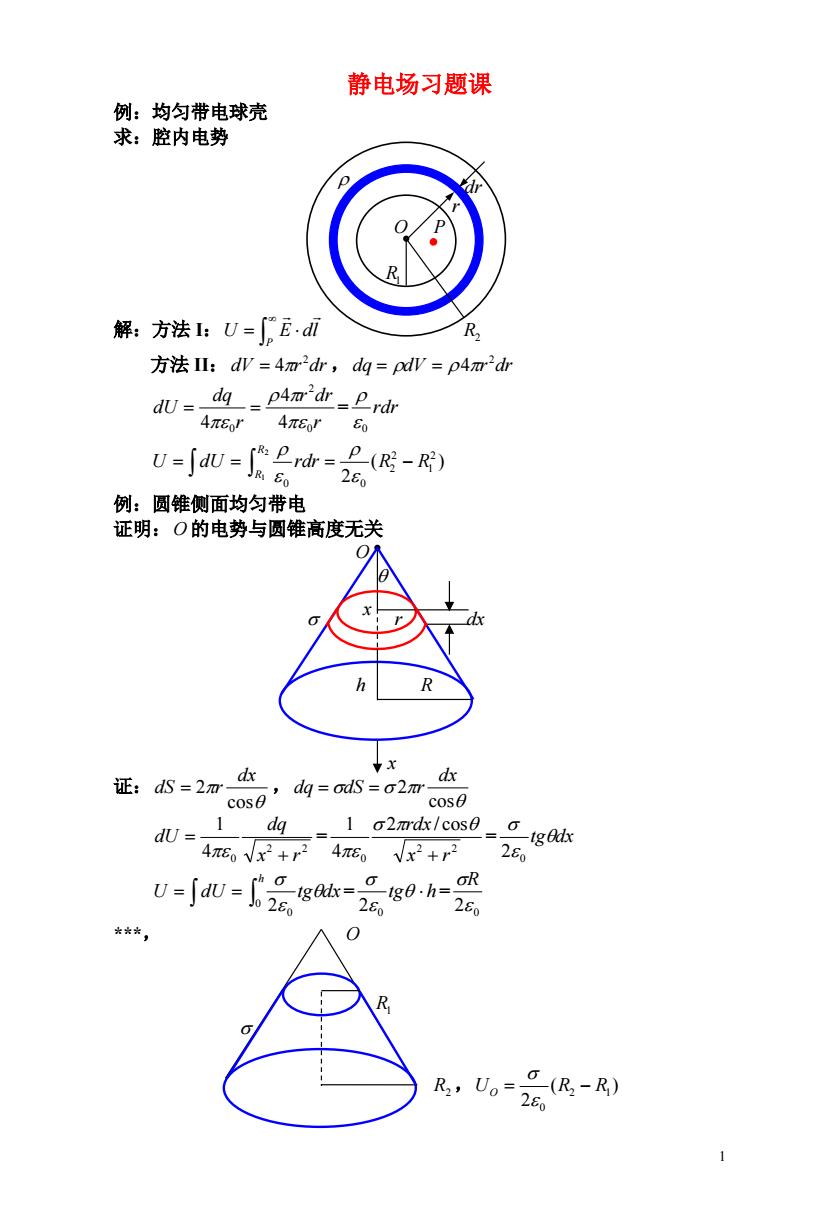
静电场习题课 例：均匀带电球壳 求：腔内电势 解：方法：U=Ed R 方法l:dW=4m2dr,dg=pdW=p4m2dr dU=▣-p4md=卫d 4π6r4π6r80 v-fu (R:-R) 280 例：圆锥侧面均匀带电 证明：O的电势与圆锥高度无关 h R ↓x 证：dS=2m cose dq=ods=o2m cose dU 1 dq 1 o2mdx/coseo g 4πEVx2+r24π80Vx2+r2 28 U--品g=289h 280 280 (R-R) R2,U0=28 1

1 静电场习题课 例：均匀带电球壳 求：腔内电势  r O P R1 解：方法 I：    P U E dl   R2 方法 II：dV  4r 2dr ，dq dV r dr 2    4 = r r dr r dq dU 0 2 0 4 4 4       rdr 0      U dU ( ) 2 2 1 2 2 0 0 2 1 rdr R R R R        例：圆锥侧面均匀带电 证明：O的电势与圆锥高度无关 O  r dx h R 证： ，  cos 2 dx dS  r     cos 2 dx dq  dS  r = = 2 2 4 0 1 x r dq dU    2 2 0 2 / cos 4 1 x r rdx      tgdx   0 2   = =  U dU  h tg dx 0 0 2    tg  h   2 0 2 0  R ***， O R1  R2 ， ( ) 2 2 1 0 UO  R  R   x  dr x

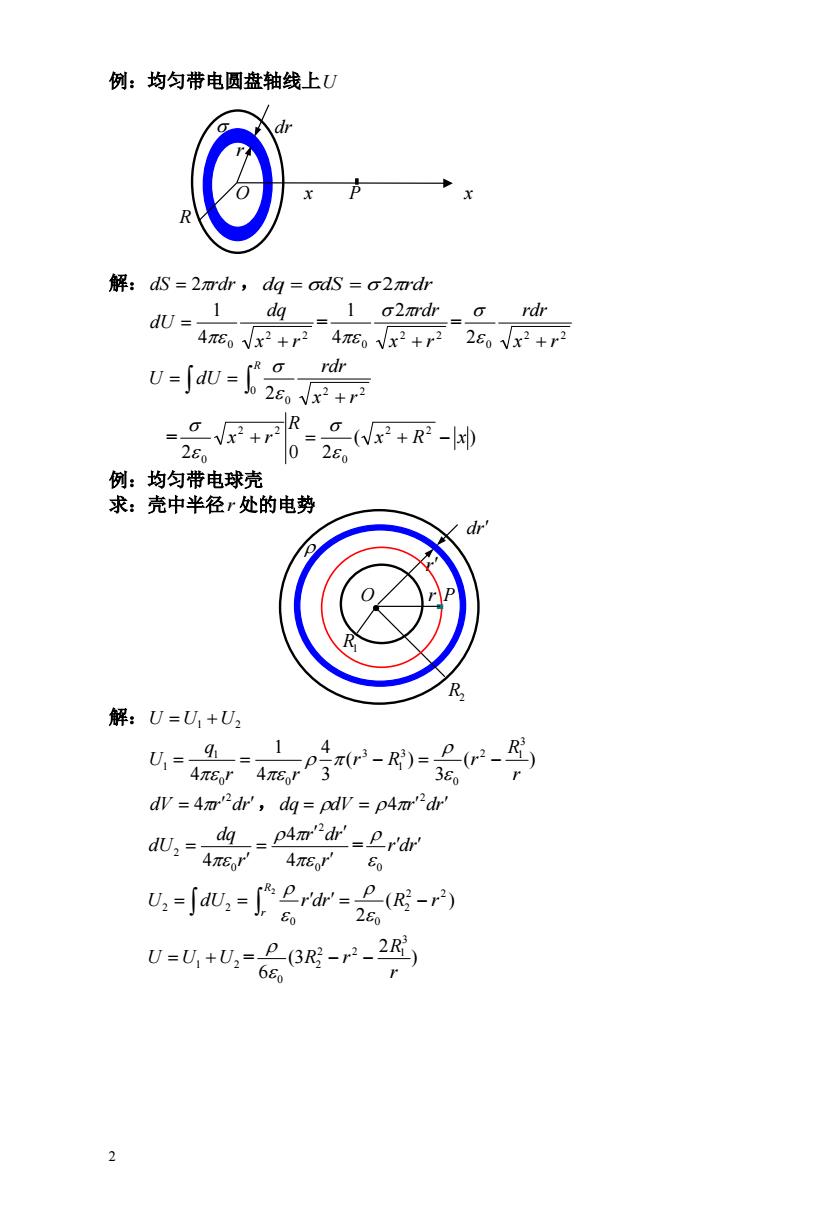
例：均匀带电圆盘轴线上U 解：dS=2mdr,dg=odS=o2mdr 1 dg dU 1 o2mdr=a rdr 476o x2+r2 476o vx2+r2 260 Vx2+r2 w--品 280 0280 例：均匀带电球壳 求：壳中半径r处的电势 dr' R 解：U=U,+U2 44P3r3-R)=2r2) U=,4= 14 38 dv =4m"dr',dq pdv pAnr"dr' ,=47 dg=p4n'd=卫rd ∫u-会r云尾- 280 U=U+U,=26R-2-2) 680 2

2 例：均匀带电圆盘轴线上U  dr r O x P x R 解：dS  2rdr ， dq  dS   2rdr = = 2 2 4 0 1 x r dq dU    2 2 0 2 4 1 x r rdr     2 2 2 0 x r rdr       U dU   R x r rdr 0 2 2 2 0   = ( ) 2 0 2 2 2 0 2 2 0 x R x R x  r        例：均匀带电球壳 求：壳中半径r 处的电势 dr  O r P R1 R2 解：U  U1 U2 ( ) 3 ( ) 3 4 4 1 4 3 2 1 0 3 1 3 0 0 1 1 r R r R r r r q U            dV  4r2dr，dq  dV  r dr 2  4 = r r dr r dq dU       0 2 0 2 4 4 4     rdr 0     U2  dU2 ( ) 2 2 2 2 0 0 2 r dr R r R r          U  U1 U2 = ) 2 (3 6 3 2 2 1 2 0 r R R  r    r

例：均匀带电球体（R,p),挖掉半径为r的小球体 d ● P石0 R R 求：（1)O处的场强 (2)P处的场强，O'OP三点共线，OP=d 解： (1)Eo=E +E2 E=Pd,方向00 380 E2=0 ,-纪4，为向0→0 (2)Ep=E+E2 E=Pd,方向0P 380 1 4 3运4d'方向p→0 E2=16(2d)P3 5关-，方0p 例：无限大带电平板，p=x,0≤x≤b S=1 P dE x 求：(1)板外的电场(2)板内的电场(3)E=0的位置 解：方法1： (1)dE= o=pld'=kax'dx, 260 dE= dx 60 E-dE-26 [Iko'dx =kb 460 3

3 例：均匀带电球体（ R ，  ），挖掉半径为r 的小球体     d d d d P O r O P O O P O r O R R 求：（1）O处的场强 （2） P 处的场强，OOP 三点共线，OP  d 解：（1） EO E1 E2       E d ，方向 0 1 3   O  O E2  0 EO d ，方向 3 0     O  O （2） EP E1 E2      E d ，方向 0 1 3   O  P 2 3 = ，方向 0 2 3 4 4 (2 ) 1 r d E     2 3 0 3 4d r   P  O EP  E1  E2 = ) ，方向 4 ( 3 2 3 0 d r d    O  P 例：无限大带电平板，   kx ，0  x  b S 1 x O x dx b P dE  x 求：（1）板外的电场（2）板内的电场（3） E  0的位置  解：方法 I： （1） ， ， 2 0   dE     1 dx  kxdx dE  kxdx 2 0 1  2 0 0 2 0 4 1 b k E dE kx dx b          = +

S=1 b (2)dE =kx'dx' 260 480480 -k(2x2-b) 480 (3)E=0,2x2-b2=0,x=(2/2)b 方法Ⅱ：高斯定理 (1) E S E b Φ=f5E·心=ES+ES=-2ES=∑g 0内 dv=Sdx',dq pav=kx'Sdx' ∑9-∫西=xsw-s6 2ES=IKS6,E=kb2 280 480 (2) n S E Ox'P b Φ=5Es=ES+Bs=1∑q 0内 由=par=a5k,g-由=a-号r E'S+ES 280 2-=4 (2x2-b) 4

4 S 1 x O x dx P b x （2）dE  kxdx 2 0 1  ( ) 2 4 4 1 2 1 2 2 0 2 0 0 0 0 b x k x k E kx dx kx dx b x x                = (2 ) 4 2 2 0 x b k   （3） E  0，2x 2  b 2  0， x  ( 2 / 2)b 方法 II：高斯定理 （1） n  E  n  n  S S S x E  O x dx b P x = + =2 =     S E dS   ES ES ES  内 i q 0 1  dV  Sdx，dq  dV = kxSdx  = = 内 i q   dq    b kx Sdx 0 2 2 1 kSb 2 ES = 2 ， 2 0 1 kSb  2 4 0 b k E   (2) n  n  E  S S x n  E  O x dx P b x = + =     S E dS   ES ES  内 i q 0 1  dq  dV = kxSdx， = = 内 i q   dq    x kx Sdx 0 2 2 1 kSx ES + ES = 2 ， 2 0 1 kSx  (2 ) 2 4 4 2 2 0 2 0 2 0 x b k b k x k E       

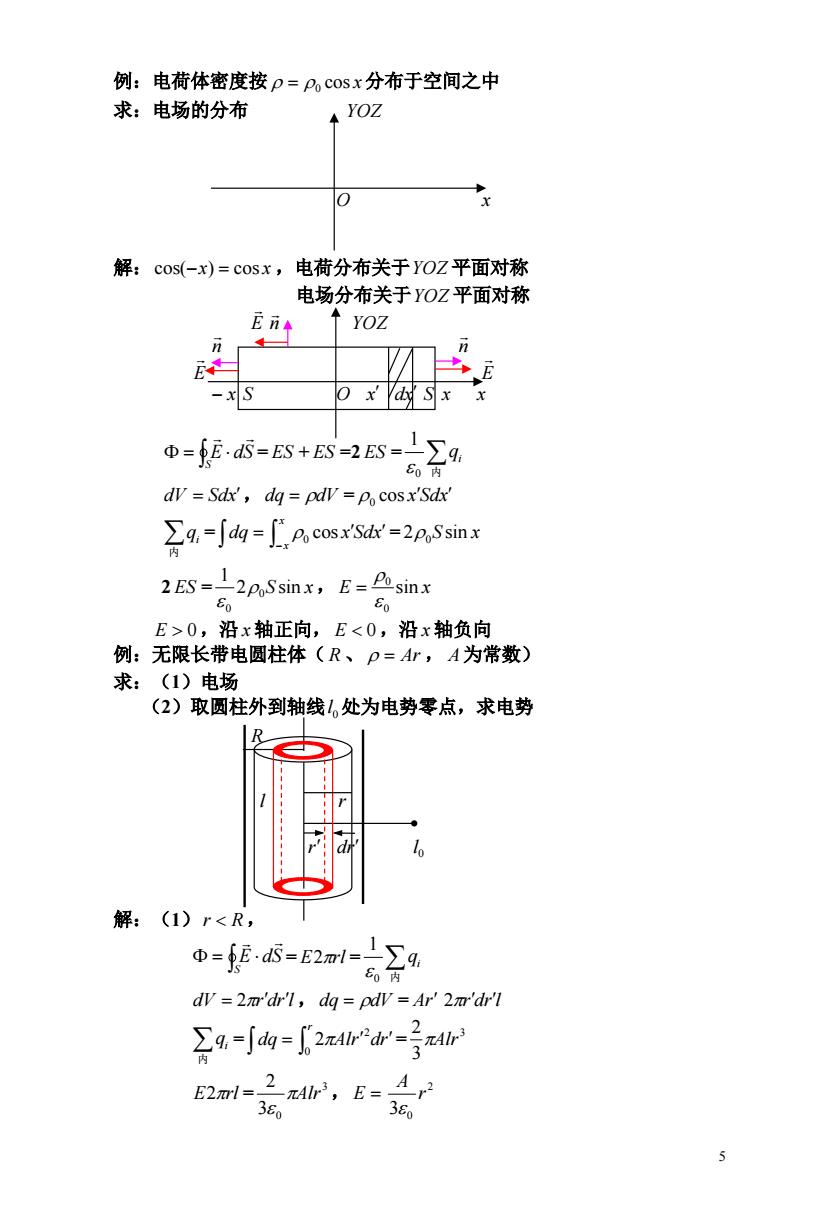
例：电荷体密度按p=Po cosx分布于空间之中 求：电场的分布 YOZ 解：cos(-x)=cosx,电荷分布关于YOZ平面对称 电场分布关于YOZ平面对称 YOZ n n E o x'dysx x Φ=fE.=-ES+ES-2BS=1∑q 0内 dv =Sdx',dq=pdv=po cosx'Sdx' ∑9，=∫a=.co=2p,Ssinx 2ES=2poSsinx,E=Posinx E>0,沿x轴正向，E<0,沿x轴负向 例：无限长带电圆柱体(R、p=Ar,A为常数) 求：（1)电场 (2)取圆柱外到轴线。处为电势零点，求电势 解： (1)r<R, Φ=fE.5=E2m1=∑9 0内 dV =2m'dr'l,dq pdv Ar'2m'dr'l ∑9=-∫a=2 rAIrdr=-号r E2a-,E A

5 例：电荷体密度按   0 cos x 分布于空间之中 求：电场的分布 YOZ O x 解：cos(x)  cos x ，电荷分布关于YOZ 平面对称 电场分布关于YOZ 平面对称 E  n  YOZ n  n  E  E   x S O x dx S x x = + =2 =     S E dS   ES ES ES  内 i q 0 1  dV  Sdx，dq  dV = cos xSdx 0  = = 内 i q   dq    x x cos x Sdx 0 2 S sin x 0 2 ES = 2 S sin x， 1 0 0   E sin x 0 0    E  0，沿 x 轴正向， E  0，沿 x 轴负向 例：无限长带电圆柱体（ R 、   Ar ， A为常数） 求：（1）电场 （2）取圆柱外到轴线l0 处为电势零点，求电势 R l r r dr 0 l 解：（1）r  R， = =     S E dS   E2rl  内 i q 0 1  dV  2rdrl ，dq  dV = Ar 2rdrl  = = 内 i q   dq Alr dr r   0 2 2 3 3 2 Alr E2rl = 3 ， 3 0 2 Alr  E  2 0 3 r A 