
运动学习题课 计算题目类型分析 一、已知运动方程,求速度和加速度 F=0,F=, d x=x(t),y=y(t),==(t) dt a =avs,a. dt dt _dt s=s0,v=, h’,s 一维直线运动:x=f0,V=血, _dt 二、已知速度,求加速度及运动方程 f=i0,a=亚,p-正-r0 dt _dt r=gudt,F=元+70h 一维直线运动 D=v0,a=i,V=五三严() d =0d,x=+y0d v=w,a-"-国.-=r dt dx dt d r-盘=re,=-fvX 分离变基法.儿高-山 →x=x(0 曲线运动,V=V(s) a,= dt ds dt ds 0 v=s=vs,∫s=∫s)dhX dt %-a=0 三、已知加速度,求速度和运动方程 a-a),a-dp =d(t)
1 运动学习题课 计算题目类型分析 一、已知运动方程,求速度和加速度 r r(t) = , dt dr V = , dt dV a = x = x(t), y = y(t) , z = z(t) dt dx Vx = , dt dy Vy = , dt dz Vz = dt dV a x x = , dt dV a y y = , dt dV a z z = s = s(t), dt ds V = , dt dV at = , 2 V an = 一维直线运动: x = f (t), dt dx V = , dt dV a = 二、已知速度,求加速度及运动方程 V V (t) = , dt dV a = , V (t) dt dr V = = = r t r dr V t dt 0 ( ) 0 , = + t r r V t dt 0 0 ( ) 一维直线运动 V = V (t), dt dV a = , V (t) dt dx V = = = x t x dx V t dt 0 ( ) 0 , = + t x x V t dt 0 0 ( ) V = V (x), dt dV a = = dx dV x V x dt dx dx dV x ( ) ( ) ( ) = V (x) dt dx V = = , dx = V (x)dt 分离变量法: = x t x dt V x dx 0 0 ( ) x = x(t) 曲线运动, V = V(s) dt dV at = = ds dV s V s dt ds ds dV s ( ) ( ) ( ) = , 2 V an = V (s) dt ds V = = , ds = V(s)dt = dt V s ds ( ) s = s(t) 三、已知加速度,求速度和运动方程 a a(t) = , dt dV a = a(t) =
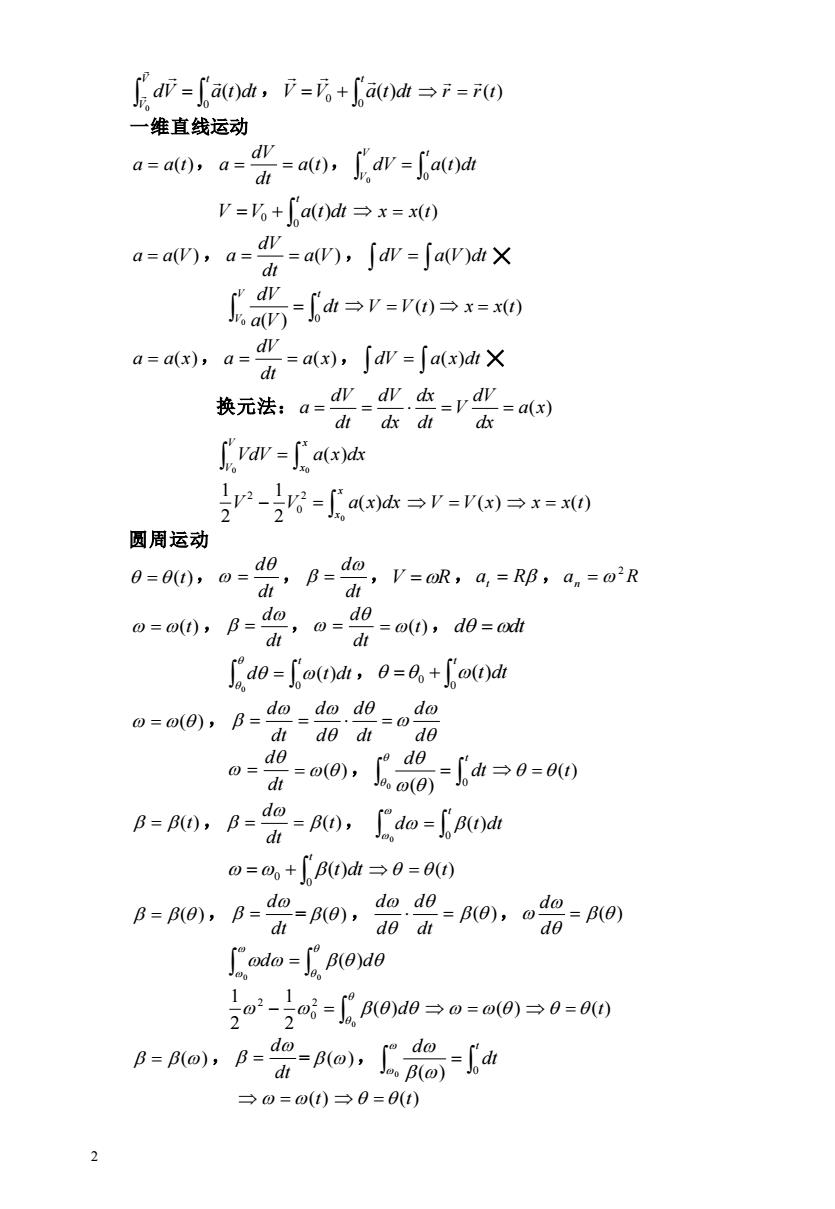
dv-fad,+fadF-F 一维直线运动 a-at).a a0).-at V=6+a0)dh→x=x0 .far-Jowx -ar-0=0 a=alx),a-4-a(x),Jdv-fa(xdrX dt 换元法:a=亚-业在-r业=a dt dx dt dx vav a(xyds r-=aa达→r===0 圆周运动 h’Bsdo 6=60,a=d0 V=R,a,=RB,an=o2R dt 0=o0,B=d0, di =0(),do=adt o-fo,-0.+focd 0=0(0),B=do=do.dodo =0 dt de dt de a0,8-a=0=a0 de 0= dt B=B),B=daB),do-)d d o=a,+0jB0)dt→0=80 a-o).)o dt da.do=p),dB) odo B(Oyo 0-时-on38=am0)s0=a0 B=Aa,B-h-e%-a →0=o(t0→0=0t) 2
2 = V t V dV a t dt 0 ( ) 0 , = + t V V a t dt 0 0 ( ) r r(t) = 一维直线运动 a = a(t), a(t) dt dV a = = , = V t V dV a t dt 0 ( ) 0 = + t V V a t dt 0 0 ( ) x = x(t) a = a(V) , a(V) dt dV a = = , dV = a(V)dt = V t V dt a V dV 0 0 ( ) V = V (t) x = x(t) a = a(x), a(x) dt dV a = = , dV = a(x)dt 换元法: a(x) dx dV V dt dx dx dV dt dV a = = = = = x x V V VdV a x dx 0 0 ( ) − = x x V V a x dx 0 ( ) 2 1 2 1 2 0 2 V = V (x) x = x(t) 圆周运动 = (t), dt d = , dt d = ,V =R ,at = R ,an R 2 = =(t) , dt d = , dt d = = (t) , d =dt = t d t dt 0 ( ) 0 , = + t t dt 0 0 ( ) = ( ) , dt d = d d dt d d d = = dt d = = ( ), = t dt d 0 0 ( ) = (t) = (t) , dt d = = (t), = t d t dt 0 ( ) 0 = + t t dt 0 0 ( ) = (t) = ( ) , dt d = = ( ) , ( ) = dt d d d , ( ) = d d = 0 0 d ( )d − = 0 ( ) 2 1 2 1 2 0 2 d =( ) = (t) = () , dt d = = (), = t dt d 0 0 ( ) =(t) = (t)
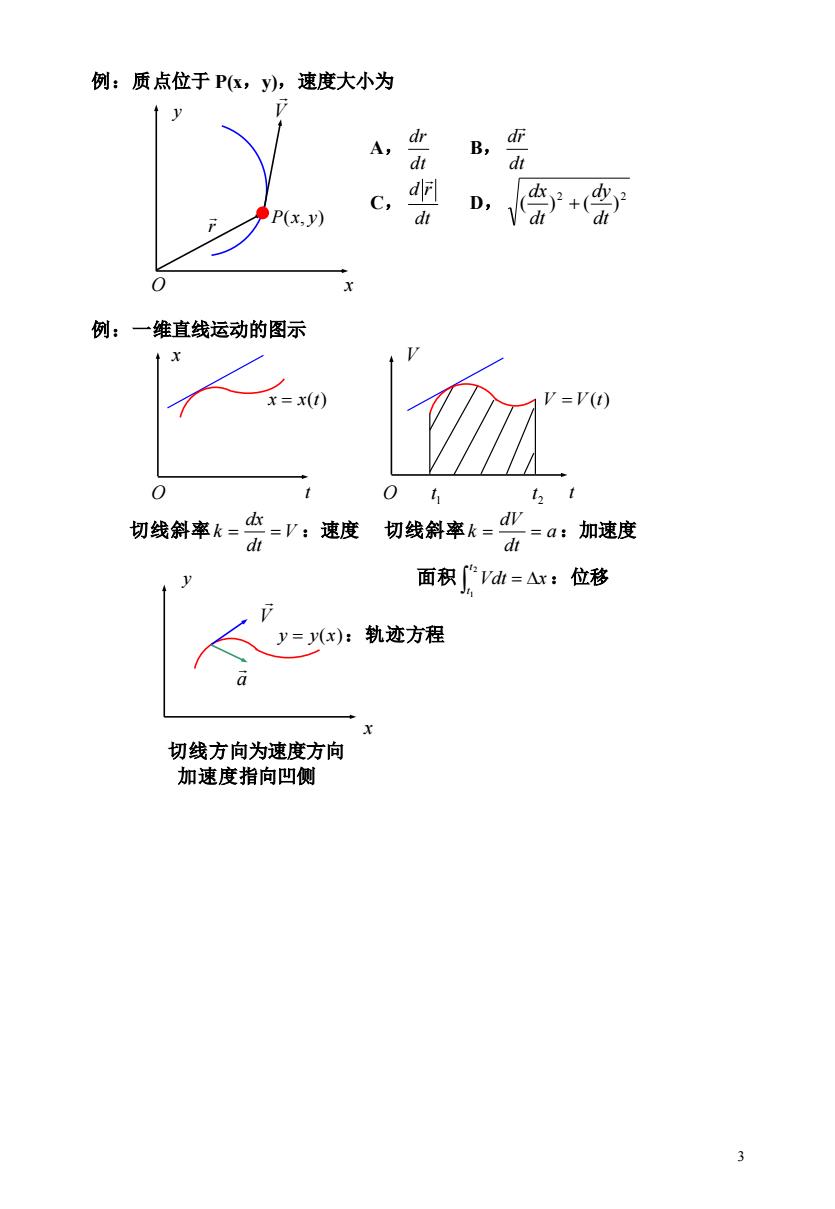
例:质点位于P(x,y),速度大小为 A, dr B, dr d d C, d D, P(x,y) dt 例:一维直线运动的图示 x=x(t) V=V(t) 0 切线斜率k=女=V:速度 切线斜率k= =a:加速度 dt di 面积Vdh=△r:位移 y=y(x):轨迹方程 a 切线方向为速度方向 加速度指向凹侧 3
3 例:质点位于 P(x,y),速度大小为 y V A, dt dr B, dt dr C, dt d r D, 2 2 ( ) ( ) dt dy dt dx + O x 例:一维直线运动的图示 x V x = x(t) V = V (t) O t O 1 t 2 t t 切线斜率 V dt dx k = = :速度 切线斜率 a dt dV k = = :加速度 y 面积 Vdt x t t = 2 1 :位移 y = y(x) :轨迹方程 x 切线方向为速度方向 加速度指向凹侧 r P(x, y) V a

一、湖中有一小船,岸边人用绳 通过高h处的滑轮拉小船, 收绳速率V。,求船离岸边s时 船速和加速度 解:r2=h2+s2,r↓ %s- _di 船速:V= 、,2r元=2sS dt v=-:-你+6,>% a= d"=d亚.k=vd业-_R dt ds dt ds α,V同方向,船作加速运动 二、质点从原点出发,以初速V沿x轴正 向运动,其加速度与速度成正比而反向 求:V(),x(①及物体静止后距原点的距离 解,a--ky=g;了七=J-k,n=-oe0 d k 0 x-1-e,1→0,V=0,物体静止,x= k *a=-kw-y-亚变=r亚,亚-k,jdm=-jkh ddkd=k’dk -V=-kx,x=V/k 三、质点作一维直线运动,已知,a=-kV2t,t=0,V='。 求:V(t) 解:a=亚-k, d 11 2Vo 2 2+kt2 四、一飞行器关闭发动机后作直线运动,其加速度大小 与速度平方成正比而反向,a=-k2,关机时,t0,V=V。 求:V()及关机后滑行的距离△x与1的关系 4
4 一、湖中有一小船,岸边人用绳 V0 通过高 h 处的滑轮拉小船, 收绳速率 V0 ,求船离岸边 s 时 船速和加速度 h r 解: 2 2 2 r = h + s , r dt dr V0 = − s 船速: dt ds V = , dt ds s dt dr 2r = 2 0 2 2 0 V s h s V s r V + = − = − , V V0 ds dV V dt ds ds dV dt dV a = = = = 0 2 3 0 2 − V s h a,V 同方向,船作加速运动 二、 质点从原点出发,以初速 V0 沿 x 轴正 向运动, 其加速度与速度成正比而反向 O V0 x 求: V (t), x(t) 及物体静止后距原点的距离 解: dt dV a = −kV = , = − V V t kdt V dV 0 0 , kt V V = − 0 ln , kt V V e − = 0 kt V e dt dx V − = = 0 , − = x t kt dx V e dt 0 0 0 , 0 0 t e k V x −kt = − (1 ) 0 kt e k V x − = − , t → ,V = 0 ,物体静止, k V x 0 = * * dx dV V dt dx dx dV dt dV a = −k V = = = , k dx dV = − , = − 0 V0 0 x dV kdx −V = −kx 0 , x V / k = 0 三、质点作一维直线运动,已知, a kV t 2 = − ,t = 0,V = V0 求: V (t) 解: kV t dt dV a 2 = = − , = − V V t ktdt V dV 0 0 2 , 2 0 2 1 1 kt V V V − = − 2 0 2 1 1 1 kt V V − + = − , 2 0 0 2 2 kV t V V + = 四、一飞行器关闭发动机后作直线运动,其加速度大小 与速度平方成正比而反向, 2 a = −kV ,关机时,t=0,V = V0 求: V (t) 及关机后滑行的距离 x 与 t 的关系 解: 2 kV dt dV a = = − , = − V V t kdt V dV 0 0 2 , kt V V V − = − 0 1
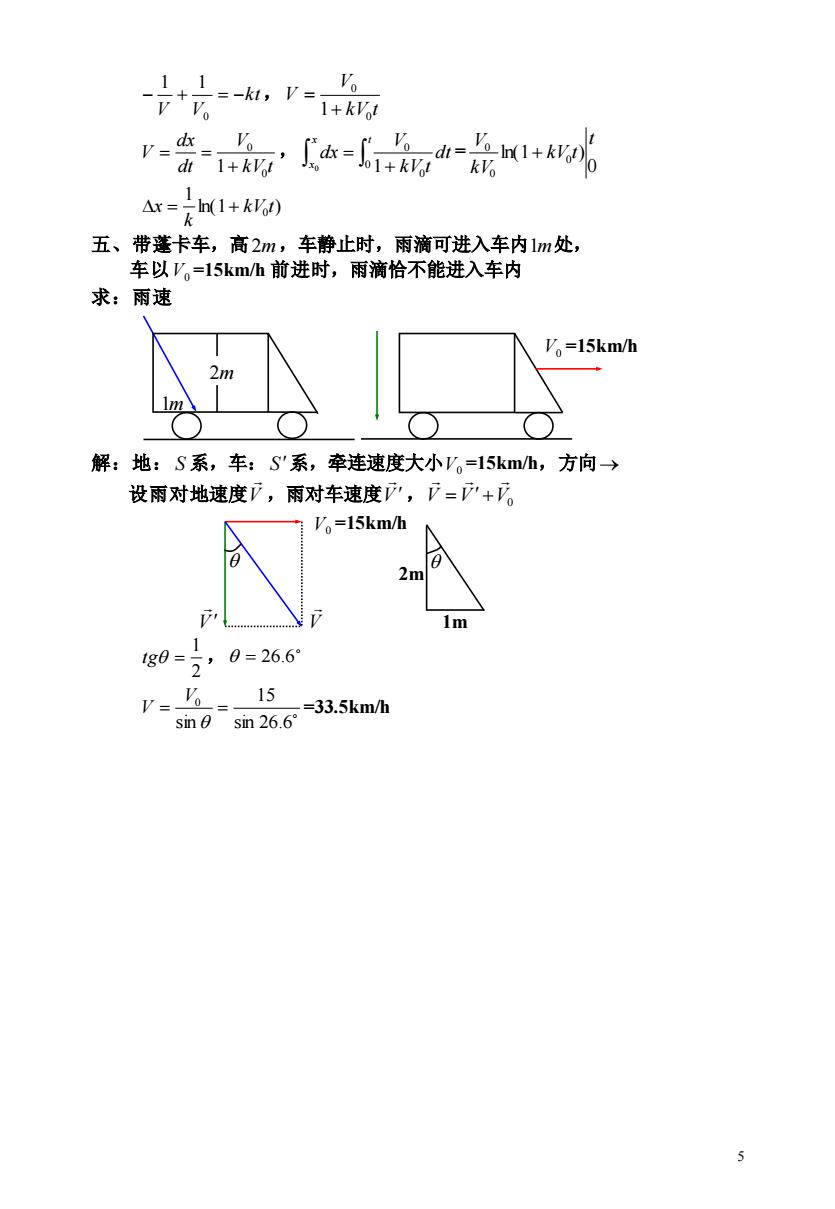
-+=-,v=6 + -1+kV dt 1+kVit A=花1+k 五、带蓬卡车,高2m,车静止时,雨滴可进入车内1m处, 车以V。=15km/h前进时,雨滴恰不能进入车内 求:雨速 Vo=15km/h 2m m 解:地:S系,车:S'系,牵连速度大小V。=15km/h,方向→ 设雨对地速度了,雨对车速度',=+。 Vo=15km/h 2m 44e4444444 1 1g6=2’0=26.6 v=% 15 =33.5km/h sin0sin26.6°
5 kt V V − + = − 0 1 1 , kV t V V 0 0 1+ = kV t V dt dx V 0 0 1+ = = , + = x t x dt kV t V dx 0 0 0 0 1 = 0 ln(1 ) 0 0 0 t kV t kV V + ln(1 ) 1 0 kV t k x = + 五、带蓬卡车,高 2m ,车静止时,雨滴可进入车内 1m 处, 车以 V0 =15km/h 前进时,雨滴恰不能进入车内 求:雨速 V0 =15km/h 2m 解:地: S 系,车: S 系,牵连速度大小 V0 =15km/h,方向 → 设雨对地速度 V ,雨对车速度 V ,V V V0 = + V0 =15km/h 2m V V 1m 2 1 tg = , = 26.6 sin 26.6 15 sin 0 = = V V =33.5km/h 1m